Esercizi sulle reti elettriche in corrente alternata (parte 1)

Esercizi sulle reti elettriche in corrente alternata (parte 1)
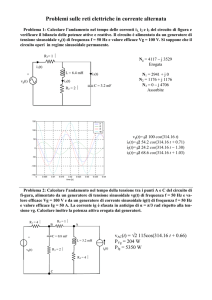
Esercizio 1: Calcolare l’andamento nel tempo delle correnti i1, i2 e i3 del circuito in figura e
verificare il bilancio delle potenze attive e reattive. Il circuito è alimentato da un generatore di
tensione sinusoidale vg(t) di frequenza f = 50 Hz e valore efficace Vg = 100 V. Si suppone che il
circuito operi in regime sinusoidale permanente.
R1= 1 Ω
Ng = 4118 − j 3529
Erogata
i1(t)
L = 6.4 mH
+
i3(t)
i2(t)
vg(t)
C = 3.2 mF
R2 = 2 Ω
N1 = 2941 + j 0
N2 = 1176 + j 1176
N3 = 0 − j 4706
Assorbite
150
i1
i2
i3
vg
100
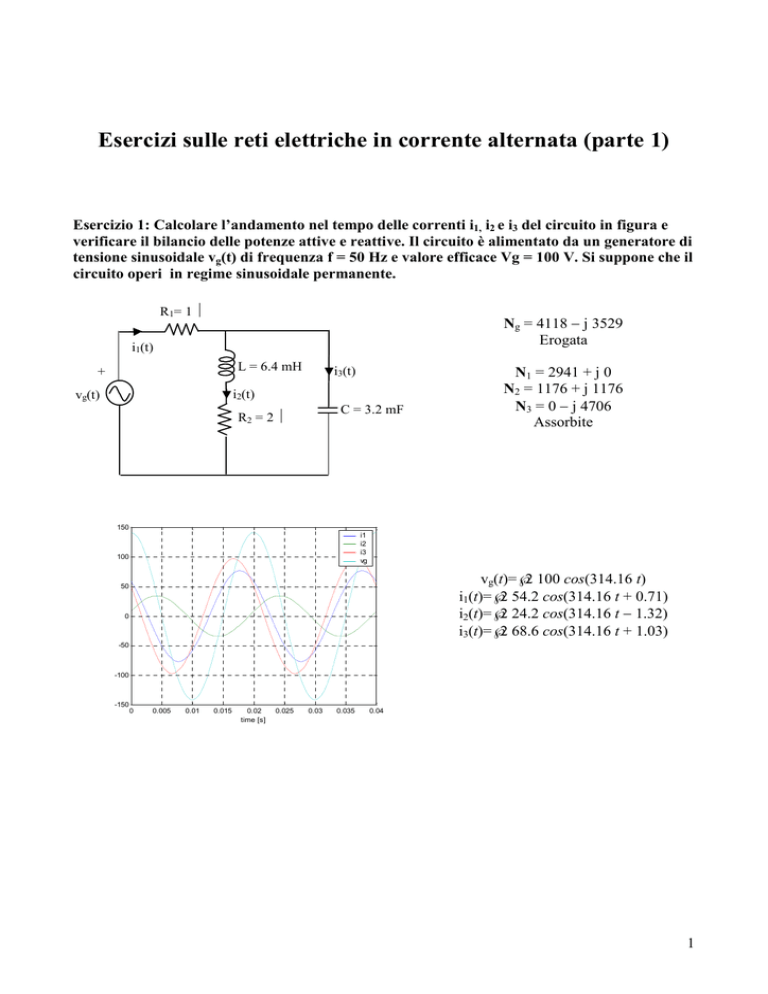
vg(t)=√2 100 cos(314.16 t)
i1(t)=√2 54.2 cos(314.16 t + 0.71)
i2(t)=√2 24.2 cos(314.16 t − 1.32)
i3(t)=√2 68.6 cos(314.16 t + 1.03)
50
0
-50
-100
-150
0
0.005
0.01
0.015
0.02
time [s]
0.025
0.03
0.035
0.04
1
Esercizio 2: Calcolare l’andamento nel tempo della tensione tra i punti C e B del circuito in
figura, alimentato da un generatore di tensione sinusoidale vg(t) di frequenza f = 50 Hz e
valore efficace Vg = 100 V, da un generatore di corrente sinusoidale ig(t) operante alla stessa
frequenza e valore efficace Ig = 50 A e da un generatore di tensione pilotato in corrente con
legge di controllo lineare. La corrente ig è sfasata in anticipo di α = π/3 rispetto alla tensione
vg. Calcolare inoltre la potenza attiva e reattiva erogata dal generatore di corrente. Si suppone
che il circuito sia in regime sinusoidale permanente.
R1 = 1 Ω
vg(t)
(k= 3 Ω)
k i2
C
R3 = 1 Ω
+
A
C = 0.8 mF
+
L = 3.2 mH
VCBmax = 125.2 V
Pig = 6604 W
Qig = − 2197 VAR
ig(t)
R2 = 2 Ω
R4 = 4 Ω
i2(t)
B
Esercizio 3: determinare la potenza istantanea e media erogata dai generatori del circuito in
figura.
Suggerimento: utilizzare il principio di sovrapposizione degli effetti.
R3
1Ω
C2
1.6 mF
potenze istantanee
pvg(t) = 40 + 20·√2 6.8 cos(ωt – 0.26)
pig(t) = −12·√2 10 cos(ωt) +
+√2 24.4 cos(ωt−0.71)·√2 10 cos(ωt)
vg(t) = 20 V
+
L
3.2 mH
R1
6Ω
R2
4Ω
C1
1.6 mF
ig(t) = √2 10 cos (ωt) A
ω = 2 π 50 rad/s
potenze medie
Pvg = 40 W
Pig = 10·24.4 cos(−0.71−0) = 185 W
2
Esercizio 4: Il circuito di figura è alimentato da un generatore di corrente sinusoidale di
valore efficace Ig = 10 A e frequenza 1 kHz e da un generatore di tensione operante alla stessa
frequenza e avente valore efficace Vg = 20 V. La tensione impressa dal generatore è in anticipo
di π/6 rispetto alla corrente impressa.
Determinare l’andamento nel tempo della corrente i e della tensione v a regime ai capi dal
dipolo RLC di figura nei tre casi decritti di seguito, prendendo come riferimento di fase quella
della tensione impressa vg. Determinare inoltre le potenze attiva e reattiva assorbite.
1. R= 2 Ω, L= 200 µH, C= 70.5 µF
2. R= 2 Ω, L= 200 µH, C= 126.6 µF
3. R= 2 Ω, L= 200 µH, C= 620.2 µF
R1
i1(t)
L1
L
R
A
Soluzione (Thevenin)
i(t)
C2
+
C
R2
vg(t)
Zeq = 1
R1 = 4 Ω
R2 = 1 Ω
L1 = 159 µH
L3 = 318 µH
C2 = 80 µF
B
I
A
+
Z
V
Eeq
k=5
L3
B
k i1(t)
Eeq = 16.7 e–j 2.19
ig(t)
Z= R+
j(ωL − 1/ωC)
Caso 1
Caso 2
Caso 3
i(t)=√2 5.3 cos(ωt − 1.87)
v(t)=√2 11.8 cos(ωt − 2.34)
P = 56.2 W
Q = −28.1 VAR
i(t)=√2 5.6 cos(ωt − 2.20)
v(t)=√2 11.2 cos(ωt − 2.20)
P = 62.3 W
Q = 0 VAR
i(t)=√2 5.3 cos(ωt − 2.52)
v(t)=√2 11.8 cos(ωt − 2.05)
P = 56.2 W
Q = 28.1 VAR
20
20
20
i
v
15
i
v
15
10
10
10
5
5
5
0
0
0
-5
-5
-5
-10
-10
-10
-15
-15
-20
0
0.5
1
1.5
t [ms]
2
2.5
3
i
v
15
-15
-20
0
0.5
1
1.5
t [ms]
2
2.5
3
-20
0
0.5
1
1.5
t [ms]
2
2.5
3
3
Esercizio 5: Determinare le potenze assorbite dai resistori R1, R3 e R6 del circuito in figura.
Suggerimento: valutare il valore delle impedenze delle serie LC e dei paralleli LC rispetto ai valori delle resistenze.
Dati:
R1 = 2 Ω
R3 = 10 Ω
R6 = 10 Ω
L = 250 µH
C = 1 µF
vg(t)=√2 10 cos ωt
ig(t)=√2 10 cos ωt
f = 1/(2π√LC) = 10066 Hz
C
R1
L
+
L
vg(t)
L
R3
C
C
ig(t)
R6
Soluzione
P1 = 50 W
P3 = 0 W
P6 = 0 W
Esercizio 6: Calcolare l’andamento nel tempo della corrente i del circuito in figura; calcolare
la potenza reattiva assorbita dall’induttore L.
Nota: sullo schema del circuito sono riportati direttamente i valori delle resistenze (in Ohm) e delle reattanze (in
Ohm) associate agli induttori (ωL) e ai condensatori (1/ωC in modulo) alla frequenza di funzionamento, e i numeri
complessi rappresentativi (valori efficaci) delle forme d’onda prodotte dai generatori di tensione (in Volt).
2
5
i
3
2
L
+
10 (1 + j)
4
+
1
20
Soluzione
i(t) = √2 2.53 cos (ωt + 1.19)
QL = 12.8 VAR
4