Esercitazione di Elettrotecnica
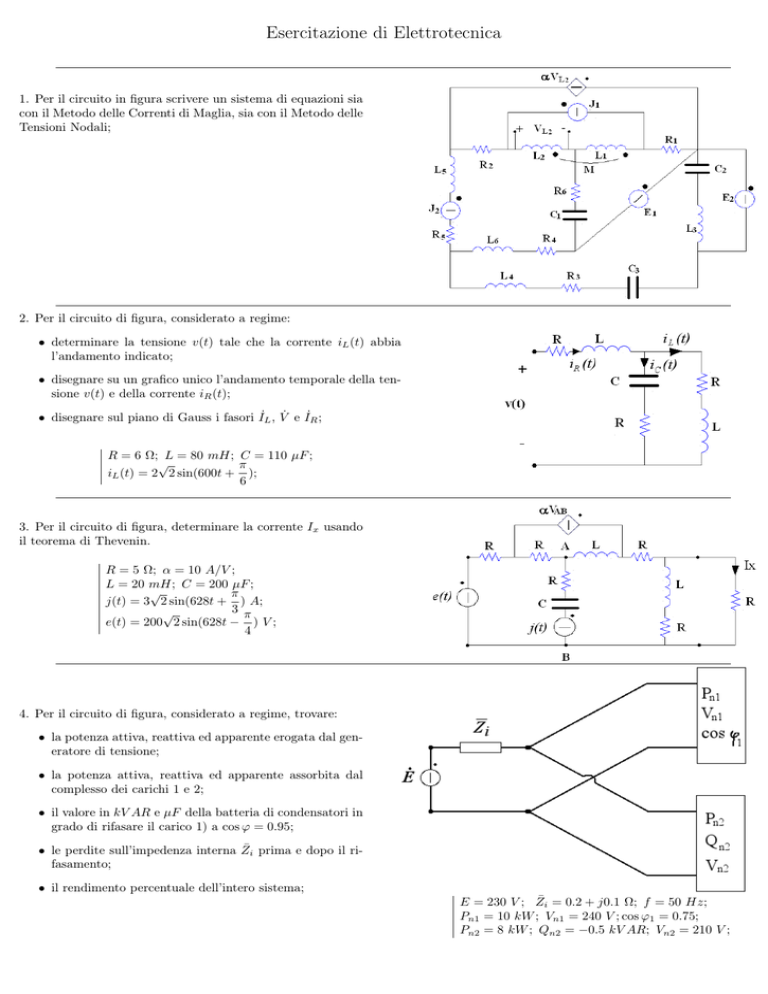
1. Per il circuito in figura scrivere un sistema di equazioni sia
con il Metodo delle Correnti di Maglia, sia con il Metodo delle
Tensioni Nodali;
2. Per il circuito di figura, considerato a regime:
• determinare la tensione v(t) tale che la corrente iL (t) abbia
l’andamento indicato;
• disegnare su un grafico unico l’andamento temporale della tensione v(t) e della corrente iR (t);
• disegnare sul piano di Gauss i fasori I˙L , V̇ e I˙R ;
R = 6 Ω; L = 80 mH; C = 110 µF ;
√
π
iL (t) = 2 2 sin(600t + );
6
3. Per il circuito di figura, determinare la corrente Ix usando
il teorema di Thevenin.
R = 5 Ω; α = 10 A/V ;
L = 20 mH; C = 200 µF ;
√
π
j(t) = 3 2 sin(628t + ) A;
3 π
√
e(t) = 200 2 sin(628t − ) V ;
4
4. Per il circuito di figura, considerato a regime, trovare:
• la potenza attiva, reattiva ed apparente erogata dal generatore di tensione;
• la potenza attiva, reattiva ed apparente assorbita dal
complesso dei carichi 1 e 2;
• il valore in kV AR e µF della batteria di condensatori in
grado di rifasare il carico 1) a cos ϕ = 0.95;
• le perdite sull’impedenza interna Z̄i prima e dopo il rifasamento;
• il rendimento percentuale dell’intero sistema;
E = 230 V ; Z̄i = 0.2 + j0.1 Ω; f = 50 Hz;
Pn1 = 10 kW ; Vn1 = 240 V ; cos ϕ1 = 0.75;
Pn2 = 8 kW ; Qn2 = −0.5 kV AR; Vn2 = 210 V ;
5. Il circuito da analizzare è a regime sotto l’effetto del generatore di tensione avente la forma d’onda periodica NON
sinusoidale indicata in figura. Determinare: a) la corrente ix (t) fino alla 9a armonica compresa (n = 9); b) il suo valore
efficace Ixef f ; c) la Potenza attiva P erogata dal generatore di tensione; d) il fattore di distorsione armonica totale (THD)
della corrente.
L = 10 mH;
C = 30 µF ;
R=2Ω
−−−−−
E0 = 100 V ;
T = 180 ms
6. Nel circuito di figura trovare la tensione vab (t) ed effettuare
la verifica sulla potenza tramite il Teorema di Boucherot.
7. Nel circuito di figura calcolare la corrente i6 (t), la potenza
P erogata singolarmente dai due generatori e l’energia elettromagnetica media W̄ immagazzinata negli elementi reattivi della rete.
E1 = 173.2 + j100 V ; E2 = 105 + j182 V ;
E3 = 50 + j86.6 V ; E5 = 28.3 − j28.3 V
Z̄1 = 2 + j1 Ω; Z̄2 = 3 − j4 Ω;
Z̄3 = 1 − j3 Ω; Z̄6 = 4 + j7 Ω;
ω = 100 rad/s; L4 = 12 mH; L5 = 10 mH; M = 8 mH;
√
e1 (t) = 230 2 cos(200t) V ;
i3 (t) = 2 Adc ;
R1 = 5 Ω; R2 = 5 Ω; R4 = 4 Ω; R5 = 6 Ω;
C1 = 200 µF ; L2 = 40 mH; L6 = 25 mH;
8. Per i circuiti di figura, determinare le correnti indicate usando i Teoremi di Thevenin e di Norton. Calcolare la potenza
P, Q e S erogata singolarmente dai generatori ed effettuare la verifica sulla potenza tramite il Teorema di Boucherot.
E1 = 100 + j70 V ; E2 = 80 + j150 V ; J1 = 3 + j2 A; Z̄1 = 2 + j1 Ω; Z̄2 = 3 − j4 Ω; Z̄3 = 1 − j3 Ω; Z̄4 = 2 + j2 Ω;
Z̄5 = 3 + j1 Ω; Z̄6 = 4 + j7 Ω; Z̄7 = 3 − j3 Ω; Z̄8 = 1 + j2 Ω; Z̄9 = 1 − j2 Ω; Z̄ = 5 + j3 Ω;
9. Per i circuiti di figura, determinare le impedenze equivalenti viste dai morsetti A − B (usare dati esercizio precedente);












