Problemi sulle reti elettriche in corrente alternata
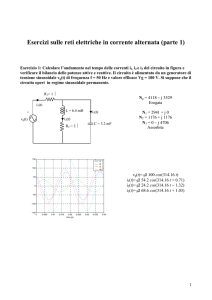
Problema 1: Calcolare l’andamento nel tempo delle correnti i1, i2 e i3 del circuito di figura e
verificare il bilancio delle potenze attive e reattive. Il circuito è alimentato da un generatore di
tensione sinusoidale vg(t) di frequenza f = 50 Hz e valore efficace Vg = 100 V. Si suppone che il
circuito operi in regime sinusoidale permanente.
R1 = 1 Ω
Ng = 4117 − j 3529
Erogata
i1(t)
L = 6.4 mH
+
i3(t)
i2(t)
vg(t)
C = 3.2 mF
R2 = 2 Ω
N1 = 2941 + j 0
N2 = 1176 + j 1176
N3 = 0 − j 4706
Assorbite
150
i1
i2
i3
vg
100
vg(t)=√2 100 cos(314.16 t)
i1(t)=√2 54.2 cos(314.16 t + 0.71)
i2(t)=√2 24.2 cos(314.16 t − 1.30)
i3(t)=√2 68.6 cos(314.16 t + 1.03)
50
0
-50
-100
-150
0
0.005
0.01
0.015
0.02
time [s]
0.025
0.03
0.035
0.04
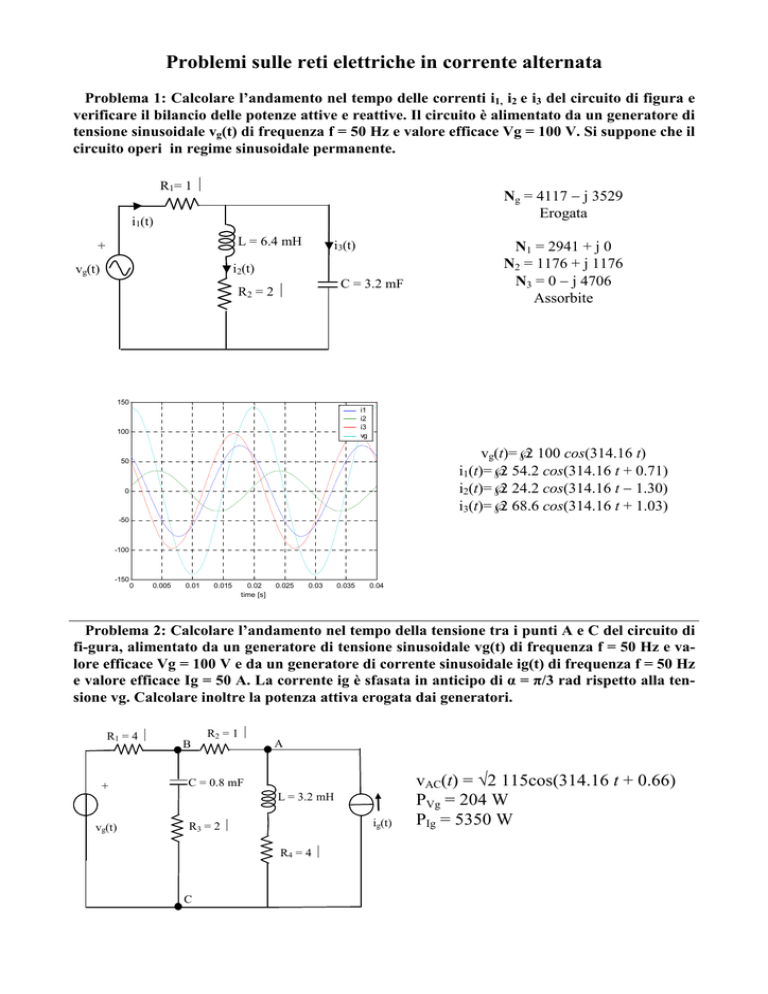
Problema 2: Calcolare l’andamento nel tempo della tensione tra i punti A e C del circuito di
fi-gura, alimentato da un generatore di tensione sinusoidale vg(t) di frequenza f = 50 Hz e valore efficace Vg = 100 V e da un generatore di corrente sinusoidale ig(t) di frequenza f = 50 Hz
e valore efficace Ig = 50 A. La corrente ig è sfasata in anticipo di α = π/3 rad rispetto alla tensione vg. Calcolare inoltre la potenza attiva erogata dai generatori.
R1 = 4 Ω
+
B
R2 = 1 Ω
A
C = 0.8 mF
L = 3.2 mH
vg(t)
R3 = 2 Ω
ig(t)
R4 = 4 Ω
C
vAC(t) = √2 115cos(314.16 t + 0.66)
PVg = 204 W
PIg = 5350 W
Problema 3: Calcolare l’andamento nel tempo della tensione tra i punti C e B del circuito di
figura, alimentato da un generatore di tensione sinusoidale vg(t) di frequenza f = 50 Hz e valore efficace Vg = 100 V, da un generatore di corrente sinusoidale ig(t) operante alla stessa frequenza e valore efficace Ig = 50 A e da un generatore di tensione pilotato in corrente con legge
di controllo lineare. La corrente ig è sfasata in anticipo di α = π/3 rad rispetto alla tensione vg.
Calcolare inoltre la potenza attiva e reattiva erogata dal generatore di corrente. Si suppone
che il circuito sia in regime sinusoidale permanente.
(k= 3 Ω)
k i2
R1 = 1 Ω
C
R3 = 1 Ω
+
A
C = 0.8 mF
+
vg(t)
L = 3.2 mH
R2 = 2 Ω
VCBmax = 125.2 V
Pig = 6604 W
Qig = − 2197 VAR
ig(t)
R4 = 4 Ω
i2(t)
B
Problema 4: Il circuito di figura è alimentato da un generatore di tensione sinusoidale vg1(t)
di valore efficace Vg1= 10 V e frequenza 1 kHz e da un generatore di tensione sinusoidale
vg2(t) operante alla stessa frequenza e avente valore efficace Vg2= 20 V . La tensione vg1(t) è
in anticipo di π/6 rispetto a vg2(t). Determinare il fasore delle correnti in tutti i rami
i1(t)
R1
L1
+
C2
vg1(t)
R2
C4
Soluzione:
L3
k i1(t)
+
vg2(t)
R1 = 4 Ω
R2 = 1 Ω
L1 = 159 µH
L3 = 318 µH
C2 = 80 µF
C4 = 80 µF
3.09 + j 4.45
+
k=5
3.79 + j 9.43
+
- 0.84 - j 5.97
Problema 5: Determinare l’andamento nel tempo della tensione tra i punti A e C. del circuito
di figura, alimentato da un generatore di tensione sinusoidale vg1(t) di frequenza f1 = 50 Hz e
valore efficace Vg1 = 100 V e da un generatore di tensione sinusoidale vg2(t) di frequenza f2
= 100 Hz e valore efficace Vg2 = 150 V; si suppone che all’istante iniziale il generatore vg1
eroghi la tensione massima e il generatore vg2 attraversi lo zero crescente
A
R2 = 2 Ω
R4 = 2 Ω
B
C1 = 1.6 mF
+
C2 = 0.8 mF
L = 3.2 mH
vg1(t)
+
vg2(t)
R1 = 2 Ω
R3 = 3 Ω
C
Soluzione:
grafico dell’andamento nel tempo di vg1(t), vg2(t) e vAC(t),
vAC(t) = = √2 62.7 cos(314.16 t + 0.54) + √2 39.4 cos(628.32 t − 1.76)
Problema 6: determinare la potenza media erogata a regime dai generatori del circuito di
figura
R3
1Ω
potenze istantanee
pvg(t) = 40 + 20·√2 6.8 cos(ωt – 0.26)
pig(t) = −12·√2 10 cos(ωt) +
+√2 24.4 cos(ωt−0.71)·√2 10 cos(ωt)
C2
1.6 mF
vg(t) = 20
+
L
3.2 mH
R2
4Ω
ig(t) = √2 10 cos (ωt)
ω = 2 π 50
C1
1.6 mF
R1
6Ω
potenze medie
Pvg = 40 W
Pig = 10·24.4 cos(−0.71−0) = 185 W
Problema 7: Con riferimento al circuito di determinare:
a – il valore efficace della tensione al secondario del trasformatore
b – la potenza attiva e reattiva erogata dal generatore
c – la potenza attiva assorbita dalla resistenza R5
1Ω
3.2 mH
1Ω
1Ω
3.2 mH
vg(t)
a:
V2 = 7.43 V
b:
Pg = 7469 W
Qg = 11179 VAR
c:
P5 = 3.94 W
R5
220 : 12
50 Hz
220 Veff
soluzione:
6.4 mH
6.4 mH
+
3.2 mH
3Ω
1Ω
Problema 8: Verificare il bilancio di potenza della rete di figura
1 : 10
1Ω
1Ω
20 Ω
T1
soluzione: potenze complesse assorbite
1Ω
1Ω
+
1 : 10
10 ∠0 V
1Ω
T2
1Ω
20 Ω
generatore:
primario trasf. T1:
secondario trasf. T1:
primario trasf. T2:
secondario trasf. T2:
– 69.56 – j 64.57
42.22 + j 42.21
– 42.22 – j 42.21
21.11 + j 21.10
– 21.11 – j 21.10
Problema 9: Il circuito di figura è alimentato da un generatore di corrente sinusoidale di
valore efficace Ig = 10 A e frequenza 1 kHz e da un generatore di tensione operante alla stessa
frequenza e avente valore efficace Vg = 20 V . La tensione impressa dal generatore è in anticipo di π/6 rispetto alla corrente impressa.
Determinare l’andamento nel tempo della corrente i e della tensione v a regime ai capi dal
dipolo RLC di figura nei tre casi decritti di seguito. Determinare inoltre le potenze attiva e reattiva assorbite.
1. R= 2 Ω, L= 200 µH, C= 70.5 µF
2. R= 2 Ω, L= 200 µH, C= 126.6 µF
3. R= 2 Ω, L= 200 µH, C= 620.2 µF
R1
i1(t)
L1
L
R
A
Soluzione (Thevenin)
i(t)
C2
+
C
R2
vg(t)
Zeq = 1
R1 = 4 Ω
R2 = 1 Ω
L1 = 159 µH
L3 = 318 µH
C2 = 80 µF
B
I
A
+
Z
V
Eeq
k=5
B
L3
k i1(t)
Eeq = 16.7 e–j 2.19
ig(t)
Z= R+
j(ωL − 1/ωC)
Caso 1
Caso 2
Caso 3
i(t)=√2 5.3 cos(ωt − 1.87)
v(t)=√2 11.8 cos(ωt − 2.34)
P = 56.2 W
Q = −28.1 VAR
i(t)=√2 5.6 cos(ωt − 2.20)
v(t)=√2 11.2 cos(ωt − 2.20)
P = 62.3 W
Q = 0 VAR
i(t)=√2 5.3 cos(ωt − 2.52)
v(t)=√2 11.8 cos(ωt − 2.05)
P = 56.2 W
Q = 28.1 VAR
20
20
20
i
v
15
i
v
15
10
10
10
5
5
5
0
0
0
-5
-5
-5
-10
-10
-10
-15
-15
-15
-20
0
0.5
1
1.5
t [ms]
2
2.5
3
-20
0
0.5
1
1.5
t [ms]
2
2.5
i
v
15
3
-20
0
0.5
1
1.5
t [ms]
2
2.5
3
Problema 10: Determinare le potenze assorbite dalle resistenze R1, R3 e R6 del circuito di figura.
C
R1
L
+
L
L
R3
vg(t)
C
C
R6
ig(t)
Dati:
R1 = 2 Ω
R3 = 10 Ω
R6 = 10 Ω
L = 250 µH
C = 1 µF
vg(t)=√2 10 cos ωt
ig(t)=√2 10 cos ωt
f = 1/(2π√LC) = 10 kHz
Soluzione
P1 = 50 W
P3 = 0 W
P6 = 0 W