Esercizi (con soluzioni) per il tutorato di
Analisi Matematica II
Laurea Magistrale in Ingegneria Edile-Architettura
Università di Pavia, a.a. 2016/2017
Prof. Laura Spinolo
Tutor: Giovanni Stagnitto
Queste pagine raccolgono gli esercizi svolti durante il tutorato dell’a. a. 2016/2017, fornitemi dalla
prof. Spinolo oppure presi da prove d’esame degli anni passati (reperibili alla pagina del prof. Gianazza,
http://arturo.imati.cnr.it/˜gianazza/anmat2.html). È presente anche una parte finale con alcuni richiami di teoria, utili per la risoluzione degli esercizi (ringrazio Nicolò Valle per questa sezione).
Sono grato a tutti coloro che vorranno segnalare gli eventuali errori (sicuramente) presenti nella stesura.
Indice
1
Notazioni
2
2
Esercizi
2.1 Equazioni differenziali . . . . . . . . . . . . . . . .
2.2 Curve e integrali di linea . . . . . . . . . . . . . .
2.3 Derivate parziali e direzionali . . . . . . . . . . . .
2.4 Massimi e minimi liberi e vincolati . . . . . . . . .
2.5 Integrali doppi e tripli . . . . . . . . . . . . . . . .
2.6 Divergenza e rotore, campi conservativi e potenziali
2.7 Serie di potenze . . . . . . . . . . . . . . . . . . .
3
3
4
4
5
6
7
9
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Soluzioni
A Alcuni richiami di teoria
A.1 Tavola delle derivate . . . . . . . . . . . . .
A.2 Equazioni differenziali ordinarie . . . . . . . .
A.3 Serie di potenze . . . . . . . . . . . . . . . .
A.4 Derivate direzionali e piani tangenti . . . . .
A.5 Operatore ∇ in coordinate cartesiane . . . .
A.6 Classificazione dei punti critici . . . . . . . .
A.7 Metodo dei moltiplicatori di Lagrange . . . .
A.8 Teorema della funzione inversa . . . . . . . .
A.9 Tecniche di integrazione e cambio di variabile
A.10 Campi conservativi, circuitazione e flusso . .
10
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
14
14
15
15
16
16
17
17
17
17
19
1
Notazioni
Le lettere in grassetto sono riservate alle quantità in R2 o R3 . Con {i, j, k} o con {x̂, ŷ, ẑ} indichiamo la base canonica di R3 , versori paralleli agli assi coordinati. Perciò un vettore generico sarà scritto
indistintamente nelle tre forme
(a, b, c)
ai + bj + ck
ax̂ + bŷ + cẑ
Se ad esempio f è una funzione da R3 in R e chiamiamo (x, y , z) le variabili di R3 indicheremo la
derivata parziale di f rispetto alla seconda variabile con una delle notazioni:
∂f (x, y , z)
∂y
Dy f (x, y , z)
D2 f (x, y , z)
Talvolta si omette l’argomento: ad esempio di scrive D2 f per indicare la funzione derivata parziale e si
scrive D2 f (x0 , y0 , z0 ) per indicare il valore che essa assume nel punto (x0 , y0 , z0 ). La derivata direzionale
nella direzione del versore u sarà indicata con
∂f (x, y , z)
∂u
Du f (x, y , z)
e la matrice jacobiana con
J f (x, y , z)
Per le derivate seconde le notazioni sono ovvie. La matrice hessiana si indica con
Hf (x, y , z)
I simboli · e × sono usati rispettivamente per il prodotto scalare in Rn e il prodotto vettoriale in R3 .
L’elemento di lunghezza per gli integrali curvilinei sarà indicato con ds e l’elemento di area per gli
integrali di superficie con dS. La scrittura dr negli integrali di circuitazione significa che r è il nome scelto
per la parametrizzazione della curva e dr = t ds dove t è il versore tangente alla curva.
2
2
Esercizi
2.1
Equazioni differenziali
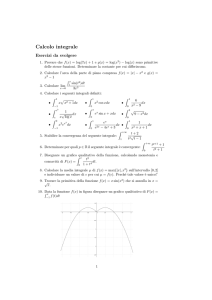
1. Calcolare l’integrale generale dell’equazione y 0 = sin t.
2. Determinare la soluzione del problema di Cauchy:
y 0 = t
1 + t2
y (0) = 2
3. Determinare la soluzione del problema di Cauchy:
y 0 = t
y2
y (0) = 1
e determinare l’intervallo massimale sul quale la soluzione è definita.
4. Determinare la soluzione del problema di Cauchy:
(
p
y 0 = 1 − y 2e t
y (0) = 1/2
5. Trovare l’integrale generale di y 0 = 2y + t 2 .
6. Risolvere il problema di Cauchy:
(
y 0 = −2y + 1
y (0) = 4
7. Mostrare come il problema di Cauchy:
(
y 0 = h(y )
y (0) = 0
con
h(y ) =
(
−1
y ≥0
1
y <0
non abbia soluzione.
8. Determinare l’integrale generale di y 00 = cos t e risolvere il problema di Cauchy:
00
y = cos t
y (0) = 1
0
y (0) = 0
9. Determinare l’integrale generale di y 00 = −10y 0 − 26y + t 2 e la soluzione del problema di Cauchy
associato con condizioni iniziali y (0) = 0 e y 0 (0) = 1.
10. Determinare l’integrale generale di y 00 = 2y 0 − 4y + e t e la soluzione del problema di Cauchy
associato con condizioni iniziali y (0) = 1 e y 0 (0) = 1.
3
11. Determinare l’integrale generale di y 00 = −6y 0 + 7y + t 2 − 1.
12. Determinare l’integrale generale di y 00 = −2y 0 − 3y + e t + 2t + 1 e la soluzione del problema di
Cauchy associato con condizioni iniziali y (0) = 0 e y 0 (0) = 0.
13. Determinare l’integrale generale di y 00 = −2y 0 − y + e t cos(t).
14. Il problema ai limiti:
00
0
y = 2y − 5y
y (0) = 0
y (π/2) = 0
ammette soluzione? Motivare la risposta.
15. (Appello del 01/09/2016, esercizio 3)
Determinare l’integrale generale dell’equazione a variabili separabili:
2
y0 = x
2.2
e −y
.
y
Curve e integrali di linea
16. Tracciare un disegno approssimativo della superficie di equazione:
x2 + y2 = z
e della curva:
r : [0, 4π] → R3 ,
r(t) = (t cos t, t sin t, t 2 ).
17. Calcolare la lunghezza della curva r : [0, 1] → R3 , definita da r(t) = (t 3/2 , cos t, sin t).
18. Siano
r : [0, 4π] → R2 ,
r(t) = (cos t, sin t);
f : R2 → R,
f (x, y ) = x 2 .
Calcolare l’integrale di linea di f lungo r.
19. (Appello del 15/09/2016, esercizio 5)
π π
Dato l’arco Γ di equazioni parametriche (x(t), y (t)) = (t cos t, t sin t) con t ∈ [ , ], calcolare
4 3
R
y
Γ 2 arctan( x ) ds.
2.3
Derivate parziali e direzionali
20. Calcolare
∂f ∂f ∂f
∂x , ∂y , ∂z
di f (x, y , z) =
xy 2 z 3
.
x2 + y2 + 1
21. Calcolare i gradienti delle seguenti funzioni:
f (x, y ) = y arctan(x 2 + y 2 );
g(x, y , z) = sin(xy + z) + 5z cos z .
4
22. Utilizzando la definizione, calcolare
∂f
∂x (0, 0)
e
∂f
∂y (0, 0)
3
3x + xy
x2 + y2
f (x, y ) =
0
quando:
(x, y ) 6= (0, 0)
(x, y ) = (0, 0)
La funzione f è continua in (0,0)?
23. Calcolare il piano tangente al grafico di f (x, y ) = cos(x 2 y ) nel punto (0, π, f (0, π)).
24. Data f (x, y , z) =
1
1
1
cos(z x)
e r = ( √ ; − √ ; √ ), calcolare
4
+z +2
3
3
3
y2
∂f
∂r .
25. Sia f (x, y , z) = x 2 y z. Calcolare l’iperpiano tangente al grafico di f in (1, 1, 1, f (1, 1, 1)).
26. Sia f (x, y , z) = y cos x + z. Determinare la direzione di massima e minima crescita di f in (0, 1, 2).
27. Sia f (x, y ) = arctan(xy ). Calcolare tutte le derivate di ordine 2 di f .
28. Calcolare lo sviluppo di Taylor di ordine 2 delle seguenti funzioni:
(a) f (x, y ) = arctan(xy ) in (0,1);
(b) f (x, y , z) = x 2 + y 3 z in (1,1,1).
2.4
Massimi e minimi liberi e vincolati
29. Sia g(x, y ) = x(x 2 − 2) + y (y 2 − 3). Determinare eventuali massimi e minimi relativi liberi della
funzione f (x, y ) = e g(x,y ) su R2 .
30. Determinare eventuali massimi e minimi relativi liberi della funzione f (x, y ) = xy e 2x+3y in R2 .
31. Dire se i seguenti insiemi sono aperti:
(a) A = {(x, y ) ∈ R2 : x 6= 0}
(b) A = {(x, y ) ∈ R2 : 0 < y < 1 − x 2 }
(c) A = {(x, y , z) ∈ R3 : 2 ≤ x < 3}
32. Determinare e classificare i punti critici delle seguenti funzioni:
(a) f (x, y ) = x 4 − x 2 + y 2
(b) f (x, y ) = sinh(x 2 ) − y 2 + y
(c) f (x, y ) = cos(πx) + sin(πy )
33. Calcolare massimo e minimo di f : A → R, ove A = {(x, y ) : x ≥ 0, y ≥ 0, y ≤ 1 − x} e
f (x, y ) = x 2 − x + y 2 + y .
34. Calcolare massimo e minimo assoluti di f sotto al vincolo g(x, y ) = 1:
(a) f (x, y ) = sinh(3x 2 + 2y ),
(b) f (x, y ) = x 3 + 2y 2 ,
g(x, y ) = x 4 + y 2 ;
g(x, y ) = 2x 2 + y 2 .
35. Determinare massimo e minimo assoluti di f (x, y ) = ln(1 + x 2 + y 2 ), nel compatto K = {(x, y ) :
x2
−1 ≤ y ≤ 1 − }.
2
5
36. Determinare massimo e minimo assoluti di f (x, y ) = e 9x
9y 2 ≤ 1}.
sin ϕ cos ϑ
37. Descrivere f : R2 → R3 con f(ϕ, ϑ) = 2 sin ϕ sin ϑ
3 cos ϕ
r cos π6
38. Descrivere f : R2 → R3 con f(r, t) = r sin π6
t
2 +4y 2
, nel compatto K = {(x, y ) : 4x 2 +
arctan(xy )
39. Calcolare la matrice jacobiana di f : R2 → R3 con f(x, y ) = sinh x
cosh y
x 2y
z − cos x
40. Calcolare la matrice jacobiana di f : R3 → R4 con f(x, y , z) =
y +z
e xz
41. Testare le ipotesi del Teorema della funzione inversa se:
ρ cos ϑ
f(ρ, ϑ, z) = ρ sin ϑ
z
f : R3 → R3 ,
42. Testare le ipotesi del Teorema della funzione inversa se:
f : R2 → R2 ,
2.5
f(x, y ) =
x
e cos ϑ
e x sin ϑ
Integrali doppi e tripli
43. Calcolare:
s
(a)
x 2 y dx dy .
[1,2]×[−1,0]
(b)
s
y 2 sin x dx dy .
s
y sinh(xy ) dx dy .
[0,π]×[0,1]
(c)
[0,1]×[0,2]
44. Calcolare:
x
1
dx dy ,
1 + x2
E
E = {(x, y ) : 0 ≤ x ≤ 5, 0 ≤ y ≤ x}.
45. Calcolare il volume di:
A = {(x, y , z) : 0 ≤ y ≤ 1, −y 2 ≤ x ≤ y 2 , 0 ≤ z ≤ y }.
46. Calcolare l’area di:
E = {(x, y ) : 0 ≤ y ≤ 2π, −y 4 ≤ x ≤ | sin y |}.
6
47. (Appello del 17/09/2015, esercizio 7)
Sia Ω il trapezio di vertici (nell’ordine) A(2,0), B(-2,0), C(-1,-1) e D(1,-1). Calcolare:
Z
(x 2 + y 2 ) dx dy .
Ω
48. (Appello del 27/01/2016, esercizio 7)
Sia Ω = {(x, y ) ∈ R2 : 1 < x 2 + y 2 < 2, |x| ≤ y }. Calcolare:
x
x 2 y dx dy .
Ω
49. Calcolare il baricentro di una lastra rettangolare individuata da [0, 1] × [0, 2] e con densità δ(x, y ) =
xy 2 + 1.
50. Calcolare massa e baricentro dell’ellissoide
x2 y2
+
+ z 2 ≤ 1, avente densità δ(x, y , z) = z 2 + 1.
4
9
51. Calcolare l’integrale di f (x, y , z) = z 2 sul volume E = {(x, y , z) : 0 ≤ x ≤ 1, z 2 + y 2 ≤ x 2 }.
52. (Appello del 15/09/2016, esercizio 7)
√
Si consideri il dominio Ω = {(x, y ) ∈ R2 : y ≥ 3x, (x − 2)2 + y 2 ≤ 4}. Utilizzando le coordinate
polari, calcolare
Z
y dx dy
Ω
53. (Appello del 24/02/2016, esercizio 7)
Dato l > 0, sia Q = [0, l] × [0, l] una lamina quadrata di densità µ(x, y ) = x 2 + y 2 . Determinarne
il baricentro.
54. (Appello del 01/09/2016, esercizio 7)
Si consideri la regione piana Ω = {(x, y ) ∈ R2 : x 2 + y 2 ≤ 4, y ≥ 0, (x − 2)2 + y 2 ≤ 4}. Utilizzando
le coordinate polari, calcolare
Z
(x 2 + y 2 ) dx dy
Ω
2.6
Divergenza e rotore, campi conservativi e potenziali
55. Calcolare il rotore di f nei tre seguenti casi:
f (x, y , z) = (y 2 z , arctan(xy z), sinh x)
f (x, y , z) = (−y 2 , x 3 + 1, cos(xz))
f (x, y , z) = (xy 3 , xy z , xz 2 )
56. Calcolare la divergenza di f nei tre seguenti casi:
f (x, y ) = (cos x, sin2 y )
f (x, y , z) = (cosh(y z), e xy , z 2 )
f (x, y , z) = (z 3 + 1, xy , xy z)
57. Determinare se i seguenti campi sono conservativi, e in caso affermativo trovare un potenziale U:
7
(a) f (x, y ) = (sin y + x 2 , x cos y + y )
(b) f (x, y , z) = (y z 3 , xz 3 + 2y z, 3xy z 2 + y 2 )
(c) f (x, y ) = (sin(xy ), cos(xy ) + y 2 )
(d) f (x, y , z) = (xy z , xz , z)
58. Calcolare il lavoro dei seguenti campi f lungo le curve parametrizzate dalle rispettive r(t) nei domini
indicati oppure descritte a parole:
(a) f (x, y ) = (y 2 , 2xy )
r (t) = (3 cos t, sin t), t ∈ [0, π/2]
(b) f (x, y , z) = (y , x, z)
r (t) = (cos t, sin t, t), t ∈ [0, 3π/2]
(c) f (x, y ) = (xy 2 , x + y )
perimetro del rettangolo [−1, 1] × [0, 1] percorso in senso orario
(d) f (x, y ) = (y sinh(xy ), x sinh(xy ) + y 2 )
circonferenza di raggio 2 e centro (1,1), percorsa in senso orario
R
59. Calcolare Σ f dS se:
• Σ è parametrizzata da g(x, y ) = (x, y , x 2 + y ) con (x, y ) ∈ [0, 1] × [0, 1] e f (x, y , z) = xy 2 .
• Σ è parametrizzata da g(ϕ, ϑ) = (cos ϑ sin ϕ, sin ϑ sin ϕ, cos ϕ) con (ϕ, ϑ) ∈ [0, π] × [0, 2π]
e f (x, y , z) = x 2 .
60. (Appello del 01/09/2016, esercizio 8)
Sia Σ la superficie di equazione z = xy con (x, y ) ∈ K = {0 ≤ x ≤ 1, 0 ≤ y ≤ x}. Calcolare:
Z
z
p
dS
1 + x2 + y2
Σ
61. (Appello del 03/09/2015, esercizio 6)
2
2
2
Si consideri la superficie Σ di √
equazione
√ x + y + z − 16 = 0. Verificare che i versori normali alla
superficie Σ nei punti P1 (0, 2 2, −2 2) e P2 (4, 0, 0) sono ortogonali.
62. (Appello del 04/09/2014, esercizio 4)
Si consideri il seguente campo con parametro α ∈ R:
α3 x
y
ω(x, y ) =
,
(x 2 + y 2 )3 (x 2 + y 2 )3
Determinare per quale valore di α il campo è conservativo in {x > 0} e in corrispondenza di tale
valore calcolare il potenziale che si annulla in (2,0).
63. (Appello del 24/02/2016, esercizio 2)
Si consideri il seguente campo definito in R2 \{(0, 0)}:
−16x 3
−8y
ω(x, y ) =
,
(x 4 + y 2 )2 (x 4 + y 2 )2
Verificare che il campo è conservativo nel suo dominio e calcolare il potenziale che si annulla in
(1,1).
8
64. Sia Σ la calotta sferica parametrizzata da g(ϕ, ϑ) = (R sin ϕ cos ϑ, R sin ϕ sin ϑ, R cos ϕ) con R >
0, ϕ ∈ [0, 2π/3], ϑ ∈ [0, 2π]. Sia n la normale a questa superficie orientata verso l’interno e
f(x, y , z) = (x, x, z 3 ). Calcolare:
ZZ
(∇ × f(x, y , z)) · n dS,
Σ
utilizzando il teorema della divergenza, oppure il teorema di Stokes oppure con un calcolo diretto.
2.7
Serie di potenze
65. Determinare gli intervalli di convergenza semplice e assoluta delle seguenti serie di potenze:
(a) (Appello del 18/09/2014, esercizio 5)
∞
X
n=0
x n+1
(2n + 1)(2n + 3)
(b) (Appello del 03/09/2015, esercizio 4)
∞
X
(x − 2)n
n3 ln2 (n + 1)
n=1
(c) (Appello del 17/09/2015, esercizio 4)
∞
X
(x − 1)2n
4n n2
n=1
(d) (Appello del 27/01/2016, esercizio 5)
∞
X
16−n (x − 6)4n
n−1
n=2
(e) (Appello del 05/04/2016, esercizio 5)
∞
X
(x − 2)2n
n2 + sin n
n=2
9
3
Soluzioni
1. ê y (t) = − cos t + k, k ∈ R.
1
2
ln(1 + t 2 ) + 2.
q
3. ê y (t) = 3 32 t 2 + 1. Intervallo massimale è tutto R.
2. ê y (t) =
4. ê y (t) = sin(e t + π/6 − 1).
5. ê y (t) = ae 2t + (− 21 t 2 − 12 t − 14 ), a ∈ R.
6. ê y (t) = 27 e −2t +
1
2
7. ê Il grafico della funzione, passando per l’origine, non può sempre decrescere nel semipiano superiore
e sempre crescere nel semipiano inferiore.
8. ê y (t) = − cos t + 2.
9. ê y (t) =
1
−5t
4394 [−37e
cos(t) + 4339e −5t sin(t) + 169t 2 − 130t + 37].
√
10. ê y (t) = e t [ 23 cos( 3t) + 31 ].
37
11. ê y (t) = c1 e −7t + c2 e t − 71 t 2 − 12
49 t − 343 , c1 , c2 ∈ R.
√
√
1 −t
12. ê y (t) = − 18
e cos( 2t) − 49 e −t sin( 2t) + 16 e t + 32 t − 19 .
13. ê y (t) = c1 e −t + c2 te −t +
4 t
25 e
sin(t) +
3 t
25 e
cos(t), c1 , c2 ∈ R.
14. ê Sı̀, ammette infinite soluzioni. Imponendo il passaggio per il punto (0,0) la soluzione diventa y (t) =
c1 e t sin(2t), con c1 ∈ R. La funzione, indipendentemente dal valore di c1 , passa già per il punto
(π/2, 0), quindi la terza condizione non aggiunge nulla di nuovo. Per fissare il valore di c1 occorre
imporre una condizione sulla derivata.
p
15. ê y (x) = ± ln(x 2 + e y (0)2 ).
16. ê DISEGNO?
Z 1
√
1
1√
4 + 9t dt =
(13 13 − 8).
17. ê
27
0 2
18. ê 2π.
Z π/3 p
2
19. ê
2t 1 + t 2 dt = (t 2 + 1)3/2 da valutarsi tra gli estremi.
3
π/4
∂f
y 2 z 3 (−x 2 + y 2 + 1) ∂f
2x(x 2 + 1)y z 3 ∂f
3xy 2 z 2
=
,
=
,
=
.
∂x
(x 2 + y 2 + 1)2
∂y
(x 2 + y 2 + 1)2 ∂z
x2 + y2 + 1
2xy
2y 2
2
2
,
+ arctan(x + y )
21. ê ∇f =
(x 2 + y 2 )2 + 1 (x 2 + y 2 )2 + 1
∇g = (y cos(xy + z), x cos(xy + z), cos(xy + z) − 5z sin(z) + 5 cos(z)).
20. ê
22. ê fx (0, 0) = 3, fy (0, 0) = 0. Per essere continua, è necessario che il limite per (x, y ) → (0, 0)
sia sempre nullo, qualunque successione di punti nel piano io scelga. Prendendo per esempio
x = y (ci stiamo avvicinando all’origine lungo la bisettrice del I-III quadrante), calcoliamo il limite
limh→0 f (h, h) = 1/2 e quindi f non è continua.
10
23. ê z = 1.
24. ê
∂f
1
=√
cos(zx)(2y − 4z 3 ) − sin(z x)(x + z)(y 2 + z 4 + 2) .
2
4
2
∂r
3(y + z + 2)
25. ê t = 2x + y + z − 3.
1
1
26. ê massima crescita: v = (0, √ , √ ). massima decrescita: −v.
2
2
2xy 3
2x 2 y 2
1
− 2 2
− 2 2
2
2y 2 + 1
(x
y
+
1)
x
(x y + 1)2
27. ê Hf =
2
2
1
2x y
2x 3 y
− 2
− 2 2
2
2
2
2
2
x y + 1 (x f = y + 1)
(x y + 1)
28. ê a) p(x, y ) = xy . b) p(x, y ) = x 2 + 3y 2 + 3y z − 6y − 2z + 3.
q
q
q
q
29. ê punto di massimo: (− 23 , −1). punto di minimo: ( 23 , 1). sella: (− 23 , 1); ( 23 , −1).
30. ê punto di massimo: (− 21 , − 13 ). sella: (0, 0).
31. ê a) aperto, b) aperto, c) né aperto né chiuso.
32. ê a) sella: (0, 0). punti di minimo: (± √12 , 0).
b) sella: (0, 12 ).
c) punti di minimo: (k, t + 12 ) con k e t dispari. punti di massimo: (k, t + 12 ) con k e t pari. punti
di sella: (k, t + 21 ) con k pari e t dispari o viceversa.
33. ê Mediante il gradiente, si trova il punto critico ( 12 , − 12 ) che però non fa parte dell’insieme A e quindi
non è da prendere in considerazione. Valendo il Teorema di Weierstrass, in quanto la funzione è
continua e l’insieme A è chiuso e limitato, abbiamo la certezza che in A la funzione f presenta
massimo e minimo assoluti, che si troveranno inevitabilmente sul bordo (se ci fosse stato un punto
critico interno ad A, sarebbe risultato dal calcolo del gradiente). Nel tratto sull’asse y la funzione
ha un punto di massimo in (0, 1) in cui vale 2 e un punto di minimo in (0, 0) in cui vale 0 (si vede
banalmente ponendo x = 0 nell’espressione della funzione). In modo analogo ci si può convincere
che lungo l’asse x la funzione ha un minimo in ( 12 , 0) in cui vale − 12 . Dall’esame degli estremi
vincolati sulla retta y = 1 − x mediante il metodo dei moltiplicatori di Lagrange, troviamo il punto
(1, 0) in cui la funzione vale 0. Pertanto, confrontando i vari punti trovati sul bordo, concludiamo
che (0, 1) è punto di massimo assoluto e ( 21 , 0) è punto di minimo assoluto.
34. ê a) [possiamo trovare punti di massimo e minimo di 3x 2√+2y dato che sinh è una funzione monotona]
√
3
2
, √ ). minimo assoluto = −2 nel punto
massimo assoluto = sinh( 13) nel punto (x, y ) = ( √
4
13
13
1
(x, y ) = (0, −1). b) massimo assoluto = 2 nei punti (x, y ) = (0, ±1). minimo assoluto = − √
2 2
1
nel punto (x, y ) = (− √ , 0).
2
35. ê massimo assoluto = ln(6) nei punti (x, y ) = (±2, −1). minimo globale = 0 nel punto (x, y ) = (0, 0).
1
36. ê massimo assoluto = e 9/4 nei punti (x, y ) = (± , 0). minimo globale = 1 nel punto (x, y ) = (0, 0).
2
37. ê ellissoide con rx = 1, ry = 2, rz = 3. DISEGNO?
11
38. ê piano verticale (le prime due coordinate individuano una retta nel piano xy - ricordarsi che r può
anche essere negativo in questo caso - mentre t spazza verticalmente ogni punto della retta).
DISEGNO?
x
y
(1 + x 2 y 2 ) (1 + x 2 y 2 )
39. ê J f = cosh x
0
0
sinh y
2xy x 2
0
sin x 0
1
40. ê J f =
0
1
1
ze xz 0 xe xz
41. ê Il Teorema della funzione inversa è applicabile in tutti i punti con ρ 6= 0, dal momento che in questo
caso si annulla lo jacobiano della funzione. Il punto (0, 0, 0) è immagine di tutti i punti del tipo
(ρ = 0, ϑ qualsiasi, z = 0) e quindi la funzione non è iniettiva, e quindi non invertibile in un intorno
di questi punti.
42. ê Il Teorema della funzione inversa è applicabile in tutti i punti.
43. ê a) −7/6 b) 2/3 c) sinh(2) − 2
44. ê ln(26)/2.
45. ê 1/2.
46. ê 4 + 32π 5 /5.
Z 0 Z y +2
10
.
47. ê
(x 2 + y 2 ) dx dy =
3
−1 −y −2
Z
3π/4 Z
48. ê
π/4
1
√
2
ρ4 cos2 ϑ sin ϑ dρ dϑ =
√
1
(8 − 2).
30
10
17 6
. (xb , yb ) = ( , ) ' (0.57, 1.2).
3
30 5
Z π Z 2π Z 1
48π
6ρ2 sin ϕ(ρ2 cos2 ϕ + 1) dρ dϑ dϕ =
50. ê M =
. (xb , yb , zb ) = (0, 0, 0) [guardando la
5
0
0
0
densità notiamo subito che non compaiono la x e la y, quindi il baricentro deve essere sull’asse z;
osservando poi la dipendenza da z la densità è simmetrica rispetto al piano xy e quindi il baricentro
è l’origine].
Z 1 Z x Z 2π
π
51. ê
ρ(ρ sin ϑ)2 dx dρ dϑ =
.
20
0
0
0
Z π/2 Z 4 cos ϑ
1
52. ê
ρρ sin ϑ dρ dϑ = .
3
π/3
0
49. ê M =
2l 4
5 5
. (xb , yb ) = ( l, l) [il centro di massa ha xb = yb poiché la retta x = y è un asse di
3
8 8
simmetria del sistema].
Z π/2 Z 4 cos ϑ
Z π/3 Z 2
π
π
7√
2
54. ê
ρ(ρ ) dρ dϑ +
ρ(ρ2 ) dρ dϑ = 8 +
−
3.
3
16 64
π/3
0
0
0
53. ê M =
12
64
3
πR2 . Usare il teorema della divergenza porta ad affermare che il flusso attraverso la calotta sferica
4
è opposto al flusso attraverso la base circolare della calotta - che è più facile da calcolare - dopo
aver trovato un’opportuna parametrizzazione (per esempio utilizzando una coordinata ρ radiale e
l’angolo ϑ). Usare il teorema del rotore invece permette di ridurre il calcolo del flusso al calcolo
della circuitazione lungo la circonferenza a base della calotta: anche in questo caso è necessario
parametrizzare opportunamente questa curva per esempio attraverso l’angolo ϑ.
65 a) R = 1, in x = ±1 converge.
b) R = 1, in |x − 2| = ±1 converge.
2
, per |y | ≤ 1 converge.
c) definita y = (x−1)
4
4
d) definita y = (x−6)
16 , per |y | < 1 converge, in y = 1 non converge, mentre in y = −1 converge.
e) definita y = (x − 2)2 , per |y | ≤ 1 converge.
13
A
Alcuni richiami di teoria
In questi appendici riassumiamo i più importanti risultati teorici e richiamiamo le formule più significative.
B: per brevità, trascuriamo in alcuni casi le ipotesi matematiche necessarie che stanno alle spalle di
alcune formule. Il lettore resti sempre vigile, pronto a verificare di volta in volta l’effettiva applicabilità di
ogni espressione o procedimento.
A.1
Tavola delle derivate
Se letta da destra verso sinistra è una tavola delle primitive...
f (x)
f 0 (x)
f (x)g(x)
f 0 (x)g(x) + f (x)g 0 (x)
f (g(x))
f 0 (g(x))g 0 (x)
f (x)
g(x)
f 0 (x)g(x) − f (x)g 0 (x)
[g(x)]2
f −1 (x)
1
f
0 (f −1 (x))
x α+1
(α + 1)x α
ex
ex
1
x
ln(x)
sin(x)
cos(x)
cos(x)
− sin(x)
tan(x)
1 + tan2 (x) =
1
cos2 (x)
cosh(x)
sinh(x)
sinh(x)
cosh(x)
tanh(x)
arccos(x)
1 − tanh2 (x) =
1
cosh2 (x)
1
−√
1 − x2
√
arcsin(x)
1
1 − x2
1
1 + x2
arctan(x)
14
A.2
Equazioni differenziali ordinarie
Presentiamo alcune categorie di equazioni con rispettivi metodi risolutivi.
• A variabili separabili: sono equazioni del tipo: y 0 (t) = g(y ) · h(t). Si risolvono uguagliando:
Z t
Z y (t)
dy
=
h(s) ds.
c
y (c) g(y )
dove c è una generica costante arbitraria, che può essere posta uguale a 0.
• Lineari di secondo grado a coefficienti costanti: sono equazioni del tipo:
a2 y (2) (t) + a1 y (1) (t) + a0 y (t) = f (t),
dove gli ai per i = 0, 1, 2 sono numeri reali, mentre f : I → R è una funzione continua su intervallo
aperto I assegnato.
Le soluzioni in generale possono essere scritte come soluzione dell’equazione omogenea (cioè quella
in cui f (t) = 0) più una soluzione particolare della specifica equazione.
Per la soluzione omogenea, occorre considerare il polinomio caratteristico associato:
a2 λ2 + a1 λ + a0 = 0.
A seconda del segno del determinante, le soluzioni si scrivono come combinazione lineare di specifici
termini, in base al seguente schema:
– ∆ > 0 → 2 soluzioni reali r1 e r2 → sol. om. della forma ae r1 t + be r2 t ;
– ∆ = 0 → 1 soluzione reale r con doppia molteplicità → sol. om. della forma ae r t + bte r t ;
– ∆ < 0 → 2 soluzioni complesse r± = α±i β → sol. om. della forma ae αt cos(βt)+be αt sin(βt).
Per la soluzione particolare, si considera una yp di prova, che conterrà alcuni parametri incogniti
ed assumerà una forma diversa in base all’espressione esplicita della f (t). Inserendo la soluzione di
prova all’interno dell’equazione, si determinano i parametri incogniti della soluzione di prova. Alcuni
casi:
– f (t) = polinomio → yp (t) = at 2 + bt + c;
– f (t) ∝ e γt con γ non soluzione del polinomio caratteristico → yp (t) = ce γt ;
– f (t) ∝ e γ1 t cos(γ2 t) oppure f (t) ∝ e γ1 t sin(γ2 t) → yp (t) = e γ1 t (a cos(γ2 t) + b sin(γ2 t))
[alternativamente yp (t) = ce t(γ1 +iγ2 ) e poi prendo parte reale oppure immaginaria a seconda
rispettivamente del coseno o del seno nel termine f (t)].
A.3
Serie di potenze
Assumendo noti le nozioni (in particolare quelle di convergenza semplice o assoluta), ricordiamo prima i
risultati più importanti riguardanti le serie numeriche e in seguito i punti fondamentali necessari a risolvere
gli esercizi sulle serie di potenze.
P
P
• Criterio del confronto: considerate due serie ak e bk a termini non negativi tali che ak ≤ bk , se
la maggiorante converge la minorante converge (e se la minorante diverge la maggiorante diverge).
• Criterio di Leibniz: se una successione monotona {ak } è decrescente e infinitesima, allora la
seguente serie converge:
n
X
(−1)k ak .
k=0
15
P
• Criterio del rapporto: considerata una serie a termini positivi
ak tale che esista il limite:
an+1
lim
= l,
n→∞ an
allora la serie converge se l < 1 e diverge se l > 1 (non si può dire nulla se l = 1).
P
n
• Data la serie ∞
n=0 an (x − x0 ) , esiste un unico numero R ≥ 0 (oppure R = +∞) tale che:
– la serie converge assolutamente per ogni x che verifica |x − x0 | < R;
– la serie non converge per ogni x che verifica |x − x0 | > R.
Tale numero è detto raggio di convergenza ed è dato, qualora esistano i limiti scritti, dalla seguente
formula:
p
1
= lim n |an | (criterio della radice).
R n→∞
A.4
Derivate direzionali e piani tangenti
Sia f : Rn → R differenziabile e sia r = (r1 , r2 , . . . , rn ) un versore (cioè un vettore con modulo unitario)
assegnato. Allora la derivata direzionale di f lungo la direzione di r si calcola come segue:
∂f
∂f
∂f
∂f
= r1
+ r2
+ · · · + rn
,
∂r
∂x1
∂x2
∂xn
∂f
è la usuale derivata parziale rispetto alla i-esima componente.
dove ∂x
i
Piano tangente. La formula generale per l’iperpiano tangente al grafico di una funzione f : Rn → R
differenziabile e passante per il punto (x̄, f (x̄)) è la seguente:
y − f (x̄) =
n
X
∂f
(x̄)(xi − x̄i ).
∂xi
i=1
Casi particolari di questa formula sono i seguenti:
• f : R → R: il grafico della funzione è in 2 dimensioni e l’iperpiano è la retta tangente alla curva
grafico della funzione. Ci riconduciamo alla nota formula:
df
(x̄)(x − x̄).
y − f (x̄) =
dx
• f : R2 → R: il grafico della funzione è in 3 dimensioni e l’iperpiano è il piano tangente alla superficie
grafico della funzione. La formula diventa:
df
df
(x̄)(x1 − x̄1 ) +
(x2 − x̄2 ).
y − f (x̄1 , x̄2 ) =
dx1
dx2
A.5
Operatore ∇ in coordinate cartesiane
Il gradiente di una funzione f : R3 → R, la divergenza e il rotore di una funzione F : R3 → R3 si calcolano
per funzioni differenziabili come segue:
∂f
∂f
∂f
∇f =
i+
j+
k
∂x
∂y
∂z
∂Fx
∂Fy
∂Fz
∇·F=
+
+
∂x
∂y
∂z
i
j
k
∂
∂F
∂F
∂F
∂F
∂F
∂F
z
y
x
z
y
x
∂
∂
∇ × F = ∂x ∂y ∂z = i
−
+j
−
+k
−
∂y
∂z
∂z
∂x
∂x
∂y
F F F x
y
z
dove (x, y , z) ∈ R3 e F = (Fx , Fy , Fz ).
16
A.6
Classificazione dei punti critici
Un punto x0 appartenente alla dominio di una funzione f : Rn → R è detto critico se:
∇f (x0 ) = 0
Dall’esame dell’hessiano della funzione si ricavano informazioni sulla natura del punto critico:
• Hf (x0 ) definito positivo (tutti gli autovalori sono strettamente positivi)
→ x0 punto di minimo relativo;
• Hf (x0 ) definito negativo (tutti gli autovalori sono strettamente negativi)
→ x0 punto di massimo relativo;
• Hf (x0 ) indefinito (esistono due autovalori con segno discorde)
→ x0 punto di sella (nè massimo nè minimo).
Negli altri casi occorre esaminare direttamente il comportamento della funzione nei pressi del punto critico
per determinarne la natura.
Ricordiamo che nel caso di matrici 2x2 è possibile ricavare informazioni sugli autovalori della matrice
in base alle regole seguenti:
• det < 0 → autovalori con segni discordi;
• det > 0 e Tr > 0 → autovalori concordi positivi;
• det > 0 e Tr < 0 → autovalori concordi negativi.
A.7
Metodo dei moltiplicatori di Lagrange
Supponiamo di voler massimizzare una funzione f (x, y ) sotto il vincolo g(x, y ) = 0. Il metodo consiste
nel considerare il seguente oggetto, che dipende da un parametro λ reale (il moltiplicatore):
Λ(x, y , λ) = f (x, y ) + λg(x, y ).
Risolvendo il sistema di 3 equazioni che si ottiene ponendo ∇Λ(x, y , λ) = 0, troviamo i punti candidati
a essere estremi o punti di sella (andando a calcolare esplicitamente il valore della funzione in tali punti
oppure attraverso ragionamenti qualitativi nei dintorni di questi punti possiamo concludere qualcosa
riguardo alla loro natura).
A.8
Teorema della funzione inversa
Sia f : RN → RN differenziabile con derivate continue. Se esiste un punto x0 ∈ RN tale che det J f (x0 ) 6=
0, allora esistono un intorno U di x0 e un intorno V di f (x0 ) tali che la restrizione di f ad U, ovvero la
funzione f : U → V , sia invertibile con inversa g : V → U di differenziabile. Inoltre vale J g(f (x)) =
[J f (x)]−1 per ogni x ∈ U.
A.9
Tecniche di integrazione e cambio di variabile
Verranno elencate le principali formule, senza specificare tutte le ipotesi che le rendono valide.
17
• Ricordiamo il teorema fondamentale del calcolo e le formule di integrazione per parti e per sostituzione in una dimensione.
Z b
f 0 (x) dx = f (b) − f (a) ≡ [f (x)]ba
a
Z b
Z b
0
f (x)g(x) dx = −
f (x)g 0 (x) dx + [f (x)g(x)]ba
a
a
Z
ϕ(b)
Z
f (x) dx =
ϕ(a)
b
f (ϕ(x)) ϕ0 (x) dx
a
• D dominio di R2 e T : R2 → R2 (iniettiva, con jacobiana invertibile...):
ZZ
ZZ
f (x, y ) dx dy =
f (T (x, y )) |det [J T (x, y )]| dx dy
T (D)
D
D dominio di R3 e T : R3 → R3 (si generalizza a Rn ):
ZZ
ZZ
f (x, y , z) dx dy dz =
f (T (x, y , z)) |det [J T (x, y , z)]| dx dy dz
T (D)
D
In particolare:
– Coordinate polari nel piano: T (ρ, θ) = (x(ρ, θ), y (ρ, θ)) = (ρ cos θ, ρ sin θ).
ZZ
ZZ
f (x, y ) dx dy =
f (ρ cos θ, ρ sin θ) ρ dρ dθ
T (D)
D
– Coordinate cilindriche nello spazio: T (ρ, θ, z) = (x(ρ, θ, z), y (ρ, θ, z), z) = (ρ cos θ, ρ sin θ, z).
ZZ
ZZ
f (x, y , z) dx dy dz =
f (ρ cos θ, ρ sin θ, z) ρ dρ dθ dz
T (D)
D
– Coordinate sferiche nello spazio: T (ρ, θ, ϕ) = (x(ρ, θ, ϕ), y (ρ, θ, ϕ), z(ρ, θ, ϕ))
(ρ sin θ cos ϕ, ρ sin θ sin ϕ, ρ cos θ).
ZZ
ZZ
f (x, y , z) dx dy dz =
f (ρ sin θ cos ϕ, ρ sin θ sin ϕ, ρ cos θ) ρ2 sin θ dρ dθ dϕ
T (D)
=
D
• Integrale di linea. Detto x il punto sulla curva γ ⊂ Rn , e r : [a, b] → Rn la parametrizzazione
(regolare),
Z
Z b
f (x) ds =
f (r(t)) |r0 (t)| dt
γ
a
– In particolare, se γ è curva grafico della funzione g : [a, b] → R,
Z
Z b
p
f (x, y ) ds =
f (x, g(x)) 1 + [g 0 (x)]2 dx
γ
a
Per f ≡ 1 si ottiene la lunghezza di γ.
• Integrale di superficie. Sia Σ la superficie in R3 e r : R2 → R3 la parametrizzazione. Chiamiamo u
e v i due parametri.
ZZ
ZZ
∂r(u, v ) ∂r(u, v ) du dv
f (x, y , z) dS =
f (r(u, v )) ×
∂u
∂v Σ
Ω
In particolare:
18
– Σ superficie grafico di una funzione g : Ω ⊆ R2 → R:
ZZ
ZZ
p
f (x, y , z) dS =
f (x, y , g(x, y )) 1 + |∇g(x, y )|2 dx dy
Σ
Ω
Per f ≡ 1 si ottiene l’area di Σ.
– Σ superficie cilindrica immagine di r(θ, z) = (R cos θ, R sin θ, z), θ ∈ I1 , z ∈ I2 (I1 e I2 unione
di intervalli):
ZZ
ZZ
f (x, y , z) dS =
f (R cos θ, R sin θ, z) R dθ dz
I1 ×I2
Σ
– Σ superficie sferica immagine di r(θ, ϕ) = (R sin ϕ cos ϑ, R sin ϕ sin ϑ, R cos ϕ), ϕ ∈ I1 , ϑ ∈ I2
(I1 e I2 unione di intervalli):
ZZ
ZZ
f (x, y , z) dS =
f (R sin ϕ cos ϑ, R sin ϕ sin ϑ, R cos ϕ) R2 sin ϕ dϕ dϑ
I1 ×I2
Σ
Le tecniche di integrazione adottate devono ricondurre l’integrale al calcolo di più integrali monodimensionali per i quali si possa usare il teorema fondamentale. Un integrale in 3 dimensioni, ad esempio,
dovrà essere ridotto ad un integrale triplo della forma (vi sono ovviamente diverse eccezioni, come quelle
in cui il significato geometrico di integrale permette di fornire un risultato senza procedere con il calcolo)
Z
Z Z
f (x, y , z) dx dy dz
I1
I2 (z)
I3 (y ,z)
In questo modo si integra prima rispetto ad x in un insieme che dipende da y e z, poi rispetto ad y
in un insieme che dipende da z e infine rispetto a z. Sono altrettanto valide le diverse forme ottenute
scambiando i ruoli delle tre variabili.
A.10
Campi conservativi, circuitazione e flusso
Un campo vettoriale F : A ⊆ R3 → R3 si dice conservativo se esiste un campo scalare U : A → R (detto
potenziale) tale che ∇U = F. Condizione necessaria perché un campo sia conservativo è che il suo rotore
sia nullo. Sotto opportune ipotesi di regolarità per l’insieme A, l’irrotazionalità del campo diventa anche
una condizione sufficiente per l’esistenza di un potenziale.
Introduciamo il concetto di circuitazione (spesso nel caso delle applicazioni fisiche anche chiamato lavoro):
• Sia γ una curva in R3 (si generalizza in modo banale a Rn ) e r : [a, b] → R3 la sua parametrizzazione
(regolare). Sia t il versore che in ogni punto è tangente alla curva e orientato nella direzione data
da r: t = r0 /|r0 |. La circuitazione di F : R3 → R3 lungo γ si calcola come:
Z
Z
F(x, y , z) · dr ≡
γ
Z
F(x, y , z) · t ds =
γ
b
F(r(t)) · r0 (t) dt
a
Si può dimostrare che condizione necessaria e sufficiente perché un campo vettoriale F sia conservativo
è che la circuitazione lungo una qualsiasi linea chiusa γ sia nulla:
I
F · dr.
γ
19
il che equivale a dire che l’integrale curvilineo non dipende dal cammino di integrazione, ma solo dai punti
di partenza e di arrivo. Questa formulazione consente di calcolare esplicitamente la differenza del valore
del potenziale del campo in due punti A e B:
Z B
F · dr = U(B) − U(A).
A
Introduciamo il concetto di flusso:
• Sia Σ una superficie regolare orientata in R3 e r : Ω ⊂ R2 → R3 la sua parametrizzazione. Sia n
il versore che in ogni punto è ortogonale alla superficie. Il flusso di F : R3 → R3 attraverso Σ si
calcola come:
ZZ
ZZ
∂r
∂r
F(x, y , z) · n dS =
F(r(u, v )) ·
×
du dv
∂u ∂v
Σ
Ω
I teoremi del rotore (o di Stokes) e di Gauss si possono ritenere una generalizzazione a più dimensioni
del teorema fondamentale del calcolo.
• Sia V un dominio di R3 e Σ = ∂V la superficie che lo delimita. n il versore ortogonale a Σ orientato
verso l’esterno. F : R3 → R3 . Il teorema di Gauss, sotto ipotesi di regolarità (è necessario, ad
esempio, che tutte le quantità scritte esistano) afferma che
ZZZ
ZZ
∇ · F(x, y , z) dx dy dz =
F(x, y , z) · n dS
V
Σ
• Sia γ una curva chiusa orientata in R3 e Σ una superficie avente come profilo γ. n ortogonale
alla superficie orientato in modo che, vista dalla punta di n, γ risulti percorsa in senso antiorario.
F : R3 → R3 . Il teorema del rotore, sotto ipotesi di regolarità (è necessario, ad esempio, che tutte
le quantità scritte esistano) afferma che
ZZ
I
∇ × F(x, y , z) · n dS =
F(x, y , z) · dr
Σ
γ
È importante sottolineare che circuitazione e flusso, cosı̀ come tutti gli integrali di linea e superficie,
sono quantità che coinvolgono solo le funzioni da integrare, gli insiemi di integrazione e la loro
circuitazione: pertanto esistono o non esistono ed hanno un particolare valore indipendentemente
dalla parametrizzazione della curva o superficie in gioco, purché l’orientazione non cambi.
20