Shaked e Sutton

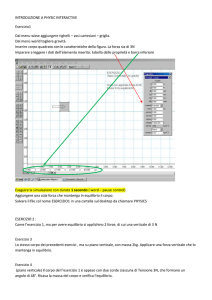
la differenziazione
verticale e la proprietà di
finitezza secondo shaked e
sutton
differenziazione verticale - parte 1
1
LA NOSTRA ROADMAP:
Il modello di Shaked e Sutton:
differenziazione verticale e concentrazione
di mercato
….l’evoluzione dal 1982
differenziazione verticale - parte 1
2
1
AVNER SHAKED
Professore di Teoria Economica,
Università di Bonn. Visiting Professor
alla Charles University, Praga.
Laurea in Matematica e Fisica e
Dottorato in Economia all’Università
Ebraica di Gerusalemme.
Editorial Board: T he Review of
Economic Studies; The Quarterly
Journal of Economics; Journal of
Economic Theory.
differenziazione verticale - parte 1
3
John Sutton
Professore di Economia e
Direttore del Dipartimento
omonimo alla London School
of Economics.
Diplomi da University
College e Trinity College di
Dublino.
Ha insegnato a alla Università
di Tokyo, alla Harvard
Business School ed alla
Università di Sheffield
differenziazione verticale - parte 1
4
2
IL MODELLO DI
SHAKED E SUTTON, 1983
IPOTESI:
separabilita’ della funzione di utilita’
nelle variabili:
Reddito
consumo
differenziazione verticale - parte 1
5
DIFFERENZIAZIONE PER QUALITA’,
CONCORRENZA DI PREZZO
E OLIGOPOLIO NATURALE
Più imprese attive sul mercato
●
Offrono beni di diversa qualità;
●
Competono sui prezzi;
●
I prezzi sono crescenti al crescere della qualità
●
La struttura dei costi dipende dal tipo di prodotto
(qualità maggiore = spesa maggiore).
differenziazione verticale - parte 1
6
3
DIFFERENZIAZIONE PER QUALITA’
COSTI FISSI
(pubblicità, R&S...)
Le spese sostenute per
incrementi di qualità
possono ricadere su:
COSTI VARIABILI
(input più pregiati,
lavoro
specializzato...)
differenziazione verticale - parte 1
7
1° Caso:
GLI ONERI RICADONO SUI COSTI FISSI
differenziazione verticale - parte 1
8
4
SHAKED E SUTTON 1982
GLI ONERI SUI COSTI FISSI
I costi medi variabili sono invarianti rispetto alla qualità,
quindi senza perdita di generalità possiamo assumere c=0
STADIO 1: scelta simultanea di entrata (non
entrata) nel mercato
STADIO 2: le imprese presenti scelgono
simultaneamente la qualità
STADIO 3: le imprese fissano i prezzi in base
alla qualità e al numero di competitori
9
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
Terzo stadio:
Le imprese scelgono i prezzi
IPOTESI DEL MODELLO:
1) beni sostituti;
2) n prodotti e n imprese;
3) prezzo pk con k= 1,…,n;
4) i consumatori hanno gli stessi gusti ma reddito diverso t,
sono distribuiti uniformemente per reddito 0 < a ≤ t ≤ b ;
differenziazione verticale - parte 1
10
5
SHAKED E SUTTON 1982
Terzo stadio:
Le imprese scelgono i prezzi
IPOTESI DEL MODELLO:
5) U(t,k) utilità per aver consumato un’unità del bene k e per aver
a disposizione t unità di reddito ( può comprare altri beni per
un valore pari a t):
U(t,k) = ukt dove U(t,0) =u0t
u0 < u1< ……. < un
6) sia
Ck =
uk
uk - uk-1
in ordine crescente di qualità
, con
Ck > 1
11
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
Il consumatore indifferente (1/2)
Ogni impresa in questo stadio fisserà il prezzo che
massimizza il proprio profitto. Il profitto dipende dal prezzo e
dal numero di consumatori che acquisteranno quel bene
Un consumatore con un livello di
reddito tk è indifferente all’acquisto
del bene k al prezzo pk rispetto a
quello del bene k-1 al prezzo pk-1, se:
U(tk- pk, k) = U(tk- pk-1, k-1)
differenziazione verticale - parte 1
12
6
SHAKED E SUTTON 1982
Il consumatore indifferente (1/2)
Ogni impresa in questo stadio fisserà il prezzo che
massimizza il proprio profitto.
Per sostituzione si ottiene: t1 = p1C1
&
tk = pk-1(1- Ck) + pk Ck
I consumatori con reddito t>tk preferiscono acquistare il bene k al
prezzo pk piuttosto che il bene k-1 al prezzo pk-1

0
  


a t1 t2……….tk….tn

b
quota di
mercato
13
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
Il consumatore indifferente (2/2)
Assumendo che i costi siano nulli, c=0, si hanno i seguenti profitti R:
R1=
p1( t2 - a)
t1 ≤ a
p1( t2 – t1)
t1 ≥ a
Rk = pk( tk+1 - tk)
1 < k< n
Rn = pn( b - tn)
Applicando le CPO e sostituendo l’espressione per tk
k
k
k
k
=
=
=
=
1
1
2…n-1
n
t2 - a - p1( C2 - 1) = 0
t2 - t1 - p1[( C2 - 1) + C1] = 0
tk+1 - tk - pk[( Ck+1 - 1) + Ck] = 0
b - tn - pnCn = 0
differenziazione verticale - parte 1
t1 ≤ a
t1 ≥ a
14
7
SHAKED E SUTTON 1982
LEMMA 1
E’ possibile dimostrare il seguente risultato:
Sia b < 4a, dato un equilibrio di Nash che coinvolge
n differenti prodotti,
allora
al più
più 2 prodotti (quelli di qualità
qualità migliore)
hanno una quota di mercato positiva all’
all’equilibrio.
equilibrio.
15
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
DIMOSTRAZIONE
Supponiamo l’esistenza di un equilibrio di Nash tale che 3
o più prodotti abbiano quota di mercato positiva;
Dalla CPO e usando la definizione di tk si ottiene:
tk+1 - 2tk - pk( Ck+1 - 1) – pk-1( Ck - 1) = 0 , per K>1
b - 2tn – pn-1( Cn - 1) = 0, per k=n
Considerato che Ck > 1, si ha che b > 2tn
e
tk+1 > 2tk
4tn-1< b
Per ipotesi [b < 4a], quindi [tn-1< a] e poiché i redditi
sono compresi tra a e b, al più due imprese coprono il
mercato.
16
differenziazione verticale - parte 1
8
SHAKED E SUTTON 1982
Caso particolare: n=2
Sia V la misura delle qualità relative dei beni 1 e 2, e del restante
bene 0, così definita:
u −u
C −1
V = u22 − u10 = C2 1 + 1
Dall’equazione del consumatore indifferente otteniamo:
p
1
=
t
C
1
1
p=
2
t2 + t1 (V −1)
C2
Utilizzando queste equazioni riscriviamo le C.P.O. per max i
profitti:
t2 = a + t1 V −1 t1 ≤ a
(
)
Impresa 1
t = t (V+1)
Impresa 2
b − 2 t = t (V −1 )
2
t ≥a
1
2
1
1
17
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
L’intersezione delle precedenti equazioni ci fornisce
l’unico equilibrio esistente (t1,t2), da cui si deriva
l’equilibrio dei prezzi (p1,p2).
L’ottimo si troverà in una delle tre regioni individuate dal grafico:
Regione I se: V ≥
Regione II se:
b+a
3a
Regione III se: V ≤
differenziazione verticale - parte 1
b+a
3a
≥V≥
b-a
3a
b-a
3a
18
9
SHAKED E SUTTON 1982
Osservazioni:
Soluzione nella regione I
t
1
=
b − 2a
3(V − 1)
t
2
=
b+a
3
Il mercato è coperto, il consumatore con minor
reddito preferisce strettamente acquistare il prodotto
di qualità inferiore.
Soluzione nella regione II
t
1
=a
t
2
=
1
[b − a(V −1)]
2
Tutti i consumatori acquistano uno dei due beni, il
mercato è coperto,il consumatore più povero è
indifferente fra l’acquistare il prodotto di qualità più
bassa o meno.
Soluzione nella regione III
t1>a
Alcuni consumatori non acquisteranno alcun bene,
perciò il mercato non sarà completamente coperto.
19
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
LEMMA 2
Assumiamo Assumiamo
che 2a<b<4a: 2a<b<4a
All’equilibrio solo 2 delle n imprese che
offrono prodotti differenziati,
raggiungono un market share positivo.
Il mercato risulta coperto.
(la coppia (p1,p2) rappresenta l’equilibrio
di Nash nei prezzi)
differenziazione verticale - parte 1
20
10
SHAKED E SUTTON 1982
Secondo stadio:
le imprese scelgono il livello di qualità
Hp:
k: numero di imprese sul mercato
xi : livello di qualità
i = 1,…,k
con
x0 < xi < x’
dove x’ è un UB esogeno
Caso k=2
R(x,y) : profitto dell’impresa che produce bene di qualità x mentre
la rivale ne produce uno di qualità y, assumendo prezzi all’equilibrio
Questa funzione ha due proprietà:
Lemma 3:
3 dati due livelli di qualità t.c. x>y, l’impresa con
il bene di qualità maggiore ha un profitto maggiore della
rivale, cioè:
R(x,y)>R(y,x)
Lemma 4:
4 i profitti di entrambe le imprese aumentano al
migliorare della qualità
delverticale
prodotto
più pregiato
differenziazione
- parte 1
21
SHAKED E SUTTON 1982
2
Il gioco G , cioè il gioco con 2 imprese a 2 stadi in cui si
scelgono prima la qualità e poi i prezzi ha un equilibrio
perfetto in strategie pure; il risultato è dato da 2 qualità
distinte e, all’equilibrio, entrambe le imprese ottengono
profitto positivo.
Il gioco Gk ha un Equilibrio di Nash con
Caso k>2
xi = x’,
1≤i≤k,
cioè tutte le imprese scelgono lo stesso livello di
qualità, il migliore
l’entrata di più di 2 imprese porta ad una configurazione in cui
il bene di qualità maggiore è disponibile a prezzo zero e tutte
le imprese ottengono profitti nulli.
differenziazione verticale - parte 1
22
11
SHAKED E SUTTON 1982
Primo stadio:
le imprese decidono se entrare
o meno nel mercato
Ipotesi:
ε>0 costo di entrata
n: numero potenziali entranti
Si può dimostrare che:
per ε>0 (abbastanza piccolo) e n>2
Esiste un equilibrio perfetto in cui 2 imprese entrano, producono
beni di qualità distinta e conseguono profitti positivi
NON esiste un equilibrio perfetto in cui le imprese entranti
siano più di 2
23
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
Conclusioni:
Il solo equilibrio perfetto nel gioco non-cooperativo a 3
stadi è quello in cui:
• esattamente 2 imprese entrano nel mercato
• esse producono beni distinti
• all’equilibrio, ottengono profitti positivi
In questo modello l’ Upper Bound sul numero di imprese
che riescono ad ottenere profitto positivo è pari a 2
ma va considerato che si è assunta una distribuzione
uniforme dei redditi tra [a,b] con la restrizione 2a<b<4a.
L’ Upper Bound cresce al crescere del range in cui variano i
redditi dei consumatori ……….
differenziazione verticale - parte 1
24
12
SHAKED E SUTTON 1982
… Quindi generalizzando si conclude che …
CONSIDERANDO LA COMPETIZIONE DI PREZZO TRA n IMPRESE
CHE
OFFRONO BENI DI QUALITA’ DIVERSA X1<X2<…<XN,
SE a>0 E L’AMPIEZZA DEL SUPPORTO DELLA DISTRIBUZIONE
DEI REDDITI E’ TALE CHE 2k-1 a< b< 2k a…
NELL’EQUILIBRIO DI PREZZO
SOLAMENTE K IMPRESE HANNO QUOTE DI MERCATO
POSITIVE PER QUALUNQUE DIMENSIONE DEL
MERCATO
PROPRIETA’ DI FINITEZZA
25
differenziazione verticale - parte 1
SHAKED E SUTTON 1982
La quota di mercato della K-esima
Impresa in ordine decrescente di
qualità include IL CONSUMATORE
CON IL REDDITO PIU’ BASSO
CONSEGUENTEMENTE
Le restanti N – k imprese
che offrono beni di qualità inferiore
NON OTTENGONO QUOTE DI
MERCATO POSITIVE
differenziazione verticale - parte 1
26
13
SHAKED E SUTTON 1982
Quando i costi medi variabili (CMV) NON DIPENDONO
dalla qualità la competizione tra i prodotti migliori riduce i loro
prezzi a un livello al quale anche il consumatore con un reddito
più basso trova conveniente acquistarli.
Poiché l’onere per incremento della qualità ricade
INTERAMENTE sui costi fissi,l’impresa con il bene più pregiato
potrebbe ridurre il proprio prezzo fino a un prezzo minimo,uguale
per tutti, pari al suo CMV.
TALE IMPRESA ACQUISISCE, IN QUESTO CASO,
TUTTO IL MERCATO
differenziazione verticale - parte 1
27
…QUINDI…
Un sufficiente divario nei CMV
tra i prodotti di qualità diversa
Impedisce un eccessivo
avvicinamento dei prezzi
dei beni
Il mercato dei prodotti
meno pregiati è, in tal
caso, garantito
differenziazione verticale - parte 1
28
14
COSTI FISSI
(pubblicità, R&S..)
Le spese sostenute per
incrementi di qualità
possono ricadere su:
COSTI VARIABILI
(input più pregiati,
lavoro specializzato..)
differenziazione verticale - parte 1
29
2° Caso:
GLI ONERI PER
INCREMENTI DI QUALITÀ
RICADONO SUI COSTI VARIABILI
differenziazione verticale - parte 1
30
15
SHAKED E SUTTON 1983
ONERI E COSTI VARIABILI
SIANO c(x) I COSTI MEDI VARIABILI IN RELAZIONE ALLA QUALITA’
X E SI SUPPONGA CHE LE QUALITA’ DEI PRODOTTI SIANO TRA
LORO DIVERSE E RICADANO IN UN INTERVALLO [X’,X’’]. LA
CONDIZIONE c’(x) ∉ [a,b] per X ∈ [X’,X’’] E’ NECESSARIA E
SUFFICIENTE PERCHE’ ESISTA UN NUMERO MASSIMO DI
PRODOTTI CON DOMANDA POSITIVA NELL’EQUILIBRIO DI NASH
NEI PREZZI, QUALUQUE SIA LA DIMENSIONE DEL MERCATO”.
Abbiamo definito:
-c(x) i costi medi variabili dipendenti dal livello di qualità
-c’(x) i costi marginali
-x il livello di qualità compreso tra x’ e x’’
-[a,b] range di variazione del reddito dei consumatori
31
differenziazione verticale - parte 1
SHAKED E SUTTON 1983
ONERI E COSTI VARIABILI
La condizione di Shaked e Sutton “c’(x) non
appartenente all’intervallo [a,b] “ è necessaria e
sufficiente perché il mercato risulti concentrato:
all’aumentare della domanda aumenta la qualità dei
beni mentre la gamma di prodotti offerti rimane
costante.
un aumento della domanda non modifica il
numero di prodotti offerti ma consente un
innalzamento dei livelli di qualita’ dei beni offerti.
Qualora la condizione non sia rispettata, il
mercato si frammenta: al crescere della dimensione del
mercato il numero di imprese
e prodotti di diversa qualita’ aumenta
differenziazione verticale - parte 1
32
16
SHAKED E SUTTON 1983
Dimostrazione (intuitiva):
SUPPONIAMO CHE AL CRESCERE DEL NUMERO DELLE
IMPRESE CORRISPONDA UN’OFFERTA DI BENI DI DIVERSA
QUALITA’ SEMPRE PIU’ RAVVICINATA
CONTRAZIONE DELLE QUOTE DI MERCATO INDIVIDUALI
LE IMPRESE REAGISCONO:
P
C(X)
Qualora c’(x)∉ [a,b] si
giunge ad una contraddizione!!
33
differenziazione verticale - parte 1
SHAKED E SUTTON 1983
Hp: p
c(x)
Ut (p,x) = t x- c(x)
Funzione di utilità del
consumatore
Ut (p,x) = tx- c(x)
t = reddito
x = qualità
ESISTE ALLORA UNA CONTRADDIZIONE CHE IMPEDISCE
DI FAR COESISTERE PREZZI PARI AI COSTI E UN
MERCATO FRAMMENTATO
Derivando la funzione di utilità del consumatore rispetto
alla qualità, otteniamo l’incremento marginale di utilità
qualora si scegliesse un bene immediamente più pregiato:
dU/dx = t - c’(x)
differenziazione verticale - parte 1
34
17
SHAKED E SUTTON 1983
L’incremento marginale di utilità qualora si
scegliesse un bene immediatamente più pregiato
è
t - c’(x)
Se c’(x)<a, t- c’(x)>0
per ogni t
Se c’(x)>b, t- c’(x)<0
∈[a,b]
per ogni t
TUTTI I CONSUMATORI
PREFERIREBBERO IL
BENE PIU’ PREGIATO
∈ [a,b]
TUTTI I CONSUMATORI
PREFERIREBBERO IL
BENE MENO PREGIATO
differenziazione verticale - parte 1
35
Se vale la condizione di Shaked è vera solo
una delle seguenti condizioni:
-c’(x)<a
-c’(x)>b
In entrambi i casi, come evidenziato, una sola
impresa ottiene profitto positivo,quella che
produce il bene più (meno) pregiato, e si
contraddice l’ipotesi di esistenza di un
mercato frammentato!
differenziazione verticale - parte 1
36
18
SHAKED E SUTTON 1983
Come conseguenza della concentrazione, abbiamo dunque le caratteristiche sopra
evidenziate, proprie di mercati per i quali vale la proprietà di finitezza.
… All’aumentare del numero dei consumatori …
… aumentano le vendite per le imprese e i profitti correnti …
… aumentano le possibilità per le imprese di sostenere costi più
elevati richiesti per produrre beni di qualità più alta …
L’AUMENTO DI DOMANDA E’ EVIDENZIATO DA UN NUMERO
COSTANTE DI BENI OFFERTI CARATTERIZZATI DA UNA
QUALITA’ VIA VIA CRESCENTE.
37
differenziazione verticale - parte 1
SHAKED E SUTTON 1983
Qualora invece violando le condizioni di Shaked e Sutton si
verifichi per qualche consumatore c’(x) = t con c’(x) ∈ [a,b],
allora la scelta di un bene di qualità x ∈[X’,X’’] (intermedia)
gli permetterebbe di massimizzare la sua utilità.
E quindi i beni di qualità intermedia otterrebbero quote di
mercato positive in equilibrio.
E vi sarebbe allora sempre spazio per un’impresa che
scegliesse un livello di qualità intermedio tra due rivali,
poiché per un prezzo sufficientemente prossimo ai propri
costi medi variabili troverebbe un gruppo di consumatori per
i quali la nuova offerta sarebbe quella più attraente sul
mercato.
Progressiva frammentazione del
mercato
differenziazione verticale - parte 1
38
19
Abbiamo supposto che ad un aumento del
numero di imprese sul mercato faccia seguito
una accesa concorrenza sui prezzi, le cui
riduzioni spingono necessariamente fuori dal
mercato i prodotti di qualità più bassa.
Tuttavia, ciò potrebbe non essere sempre vero:
potrebbe essere più conveniente accettare
l’ingresso di nuovi competitori e mantenere alti i
prezzi, piuttosto che ridurre il margine di profitto.
Shaked e Sutton si posero dunque il seguente
dilemma: cosa potrebbe accadere se in una
forma di competizione meno accesa?
39
differenziazione verticale - parte 1
Il modello di Shaked e Sutton (1983)
presuppone che:
PIU’ IMPRESE
PIU’ COMPETIZIONE
SUI PREZZI
P
C(X)
POCHE IMPRESE
REALIZZANO PROFITTI
POSITIVI
MERCATO CONCENTRATO
… ma se ci fossero forme di competizione meno accesa?...
differenziazione verticale - parte 1
40
20
SHAKED E SUTTON 1987
SHAKED E SUTTON 1987
proposero un modello in cui le imprese
differenziano i propri prodotti sia verticalmente che
orizzontalmente (sia per qualità che per varietà):
in questo modo, due beni egualmente pregiati ma
offerti in versioni diverse potrebbero coesistere con
profitti positivi, senza che la competizione riduca il
prezzo sino a spiazzare i beni di qualità più bassa
41
differenziazione verticale - parte 1
SHAKED E SUTTON 1991
Come sono strutturati i costi fissi in relazione
ai diversi tipi di differenziazione? ...
Differenziazione verticale
Differenziazione orizzontale
Mercato concentrato
Mercati frammentati
Costi fissi endogeni
Costi fissi esogeni
Tali relazioni rsono chiarite nel modello di Shaked e Sutton del 1991
differenziazione verticale - parte 1
42
21
Come sono strutturati i costi fissi in relazione ai
diversi tipi di differenziazione? ...
In un caso, i costi fissi risultano esogeni e
indipendenti dalle successive strategie di
competizione delle imprese, e pertanto non
variano in seguito all’espansione del mercato.
Nell’altro, quando vale la proprietà di finitezza
i costi fissi sono determinati endogenamente
dal livello di qualità dei prodotti offerti, ed
aumentano insieme alla dimensione del
mercato, preservandone la concentrazione.
differenziazione verticale - parte 1
43
nel Modello del 1991 evidenziarono la differenza di fondo che
conduce, in seguito alla crescita della domanda, a strutture di
mercato frammentate o concentrate.
Differenziazione orizzontale
I costi fissi risultano in
questo caso esogeni e
indipendenti dalle
successive strategie di
competizione delle
imprese, e pertanto non
variano in seguito
all’espansione del mercato,
CHE E’ ORA
FRAMMENTATO
Differenziazione verticale
Quando vale la proprietà di
finitezza i costi fissi sono
determinati
endogenamente dal livello
di qualità di prodotti offerti,
ed aumentano insieme alla
dimensione del mercato,
PRESERVANDONE QUINDI
LA CONCENTRAZIONE
differenziazione verticale - parte 1
44
22
Shaked e Sutton
In equilibrio esiste un limite superiore,
indipendente dalla qualità dei prodotti, al
numero di imprese che possono coesistere
con quote positive di mercato e prezzo
superiore o uguale ai costi variabili unitari.
differenziazione verticale - parte 1
45
Il lungo periodo
La scelta di entrare in un mercato può
essere vista come la decisione di
maggior peso e di più difficile
modificazione, e viene quindi a
caratterizzare in modo naturale
l’orizzonte di programmazione di lungo
periodo.
differenziazione verticale - parte 1
46
23