3. STRUMENTI DI BASE PER IL CALCOLO PROPOSIZIONALE
L’altra volta abbiamo esaminato le tavole di verità e provato ad effettuare su quella base i nostri primi calcoli
([ri]scoprendo alcuni principi di base). Adesso possiamo guardare alcune procedure di base, come dire
“calcoli minimi”, che si utilizzano nello sviluppo del ragionamento. Sono tutti basati sulle “tavole di verità”,
ma ne abbreviano e facilitano l’uso senza andare ad esaminarne tutti i casi (operazione particolarmente
laboriosa). Non solo: ma proprio nell’adoperare questi calcoli minimi si esplica pienamente la forza di quelle
tavole di verità, che adesso ci appariranno più naturali.
Equivalenze
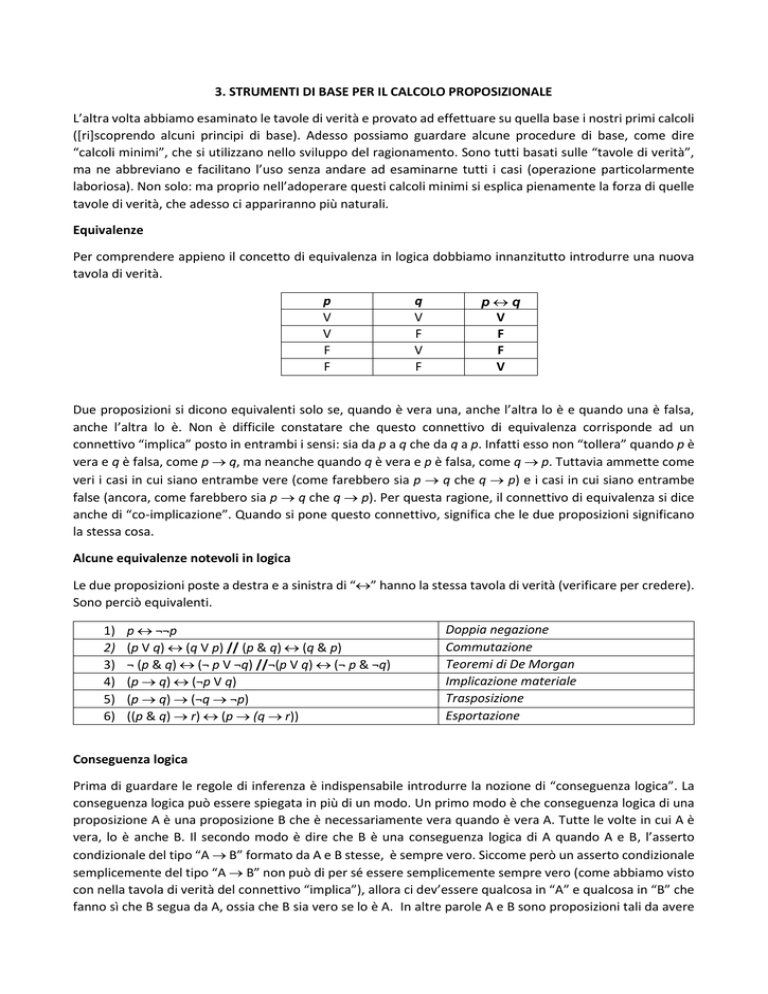
Per comprendere appieno il concetto di equivalenza in logica dobbiamo innanzitutto introdurre una nuova
tavola di verità.
p
V
V
F
F
q
V
F
V
F
pq
V
F
F
V
Due proposizioni si dicono equivalenti solo se, quando è vera una, anche l’altra lo è e quando una è falsa,
anche l’altra lo è. Non è difficile constatare che questo connettivo di equivalenza corrisponde ad un
connettivo “implica” posto in entrambi i sensi: sia da p a q che da q a p. Infatti esso non “tollera” quando p è
vera e q è falsa, come p q, ma neanche quando q è vera e p è falsa, come q p. Tuttavia ammette come
veri i casi in cui siano entrambe vere (come farebbero sia p q che q p) e i casi in cui siano entrambe
false (ancora, come farebbero sia p q che q p). Per questa ragione, il connettivo di equivalenza si dice
anche di “co-implicazione”. Quando si pone questo connettivo, significa che le due proposizioni significano
la stessa cosa.
Alcune equivalenze notevoli in logica
Le due proposizioni poste a destra e a sinistra di “” hanno la stessa tavola di verità (verificare per credere).
Sono perciò equivalenti.
1)
2)
3)
4)
5)
6)
p ¬¬p
(p V q) (q V p) // (p & q) (q & p)
¬ (p & q) (¬ p V ¬q) //¬(p V q) (¬ p & ¬q)
(p q) (¬p V q)
(p q) (¬q ¬p)
((p & q) r) (p (q r))
Doppia negazione
Commutazione
Teoremi di De Morgan
Implicazione materiale
Trasposizione
Esportazione
Conseguenza logica
Prima di guardare le regole di inferenza è indispensabile introdurre la nozione di “conseguenza logica”. La
conseguenza logica può essere spiegata in più di un modo. Un primo modo è che conseguenza logica di una
proposizione A è una proposizione B che è necessariamente vera quando è vera A. Tutte le volte in cui A è
vera, lo è anche B. Il secondo modo è dire che B è una conseguenza logica di A quando A e B, l’asserto
condizionale del tipo “A B” formato da A e B stesse, è sempre vero. Siccome però un asserto condizionale
semplicemente del tipo “A B” non può di per sé essere semplicemente sempre vero (come abbiamo visto
con nella tavola di verità del connettivo “implica”), allora ci dev’essere qualcosa in “A” e qualcosa in “B” che
fanno sì che B segua da A, ossia che B sia vero se lo è A. In altre parole A e B sono proposizioni tali da avere
una connessione che lega tra loro internamente, ed in virtù di tale connessione B è sempre vera, se è vera A.
Ad esempio “A” = “p & q” e “B” = “p”. Questo tipo di connessione, non dipende dai valori di verità di né di p
né di q, ma si pone come valido deduttivamente, perché se è vero “p & q”, sulla base delle nostre tavole di
verità, lo dev’essere anche “p” preso da solo (che principio generale è qui ripreso?). Capiamo quindi che il
connettivo “” è solo la forma esterna che assume l’asserto, e che invece c’è una connessione più intrinseca
(quale?) che collega la verità di “A” a quella di “B”. Questa connessione è una connessione di ragionamento
e la rappresenteremo con il simbolo “”. Perciò, quando incontreremo una formula del tipo “A B”, non
leggeremo semplicemente “Se A, allora B”, ma “B è conseguenza logica di A”, o “B segue da A” (come “Socrate
è mortale” segue da “Ogni uomo è mortale e Socrate è un uomo”).
Una proposizione sempre vera in logica si dice “valida”. Una che possa essere vera o falsa si dice
“soddisfacibile”. Una infine che sia sempre falsa, si dice “contraddittoria”. C’è un legame forte tra una
proposizione valida ed una contraddittoria: infatti, la negazione di una proposizione valida è contraddittoria,
e la negazione di una proposizione contraddittoria è una proposizione valida. Ciò ha avuto parecchie
conseguenze sulle modalità di calcolo. (La negazione di una proposizione soddisfacibile, com’è?)
Esempi di proposizioni valide già incontrate sono….
……………………………………………………………………………………………………………………………………………………………………….
Esempi di proposizioni contraddittorie già incontrate sono…
……………………………………………………………………………………………………………………………………………………………………….
Un esempio di una proposizione soddisfacibile è……………………………………………………………
Regole di inferenza
1)
2)
3)
4)
5)
6)
7)
8)
p & q p // p & q q
p V q , ¬p q//…
p, q (p & q)
p (p V q)
([p] … … q) (p q)
p q, p q
p q, ¬q ¬p
p q, q r p r
“semplificazione”, oppure “elimina &”
“Sillogismo disgiuntivo” oppure “elimina V”
“Congiunzione” o “inserisci &”
“Addizione” o “inserisci V”
“Inserisci ”
“Modus ponens” o “elimina ”
“Modus tollens”
“Sillogismo ipotetico”
Proviamo ora una dimostrazione diretta del “Sillogismo ipotetico”. ed una indiretta, detta “dimostrazione
per assurdo”, dello stesso.











