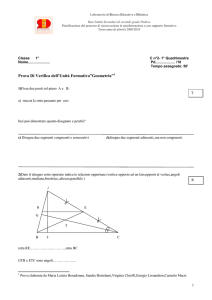
Problema:
che tipo di quadrilatero si ottiene se
si congiungono i punti medi di un
quadrilatero qualunque?
Link A FILE GEOGEBRA
Dimostrazione:
Tracciamo il segmento AC e consideriamo il triangolo ADC; per il
teorema che afferma che il segmento che ha per estremi i punti
medi di due lati di un triangolo è parallelo al terzo lato e
congruente alla sua metà, il segmento HG risulta parallelo ad AC
e congruente alla metà di AC.
Consideriamo poi il triangolo ABC, per il teorema sopra citato, il
segmento EF è parallelo ad AC e congruente alla sua metà, quindi
per la proprietà transitiva del parallelismo HG è parallelo a EF e
per la proprietà transitiva della congruenza EF è congruente a HG.
Quindi EFGH è un parallelogramma perché ha una coppia di lati
opposti paralleli e congruenti.
Osserviamo anche che si può dimostrare in modo analogo a
quanto fatto sopra che i lati GF ed EH sono paralleli ed entrambi
congruenti alla metà di DB.
Il parallelogramma EFGH ha quindi i lati opposti paralleli alle
diagonali di ABCD.
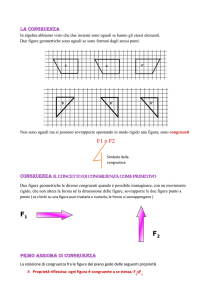
Caso particolare 1:
cosa accade se ABCD ha le diagonali congruenti?
Link a FILE GEOGEBRA
Teorema: Se ABCD ha le diagonali congruenti
allora EFGH è un rombo.
Dimostrazione:
Per il teorema precedentemente dimostrato,
EFGH è un parallelogramma. EH è congruente a
FG che è congruente a metà AC, e EF è
congruente a HG che è congruente a metà BD. Ma
AC è congruente a BD, quindi per la proprietà
transitiva EF è congruente a GH che è congruente
a FG che è congruente a EH.
Quindi EFGH è un ROMBO.
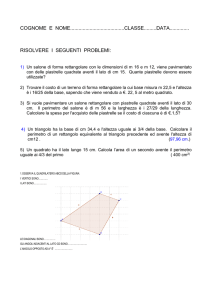
Caso particolare 2:
E cosa accade se ABCD ha le diagonali perpendicolari?
Link a FILE GEOGEBRA
Teorema: Se ABCD ha le diagonali perpendicolare allora
EFGH è un rettangolo.
Dimostrazione:
Per quanto già dimostrato prima,sappiamo già che EFGH
è un parallelogramma per il teorema di Talete. Quindi
sappiamo che i segmenti EF e HG sono paralleli alla
diagonale AC e che i segmenti HE e GF sono paralleli alla
diagonale BD. Sappiamo anche che le diagonali AC e BD
sono perpendicolari fra loro per ipotesi quindi il
segmento EF è perpendicolare al segmento EH perché
segmenti paralleli di segmenti perpendicolari. Quindi
EFGH è un parallelogramma avente un angolo retto.
Quindi EFGH è un RETTANGOLO.
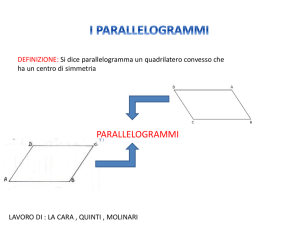
Conclusioni
ABCD è un
quadrilatero qualsiasi
IFGH è un
parallelogramma
ABCD ha le diagonali
congruenti
IFGH è un rombo
ABCD ha le diagonali
perpendicolari
IFGH è un rettangolo