Termodinamica e termochimica

Termodinamica e termochimica
La termodinamica è una scienza che studia proprietà macroscopiche
della materia e prevede quali processi chimici e fisici siano possibili, in
quali condizioni e con quali energie in gioco.
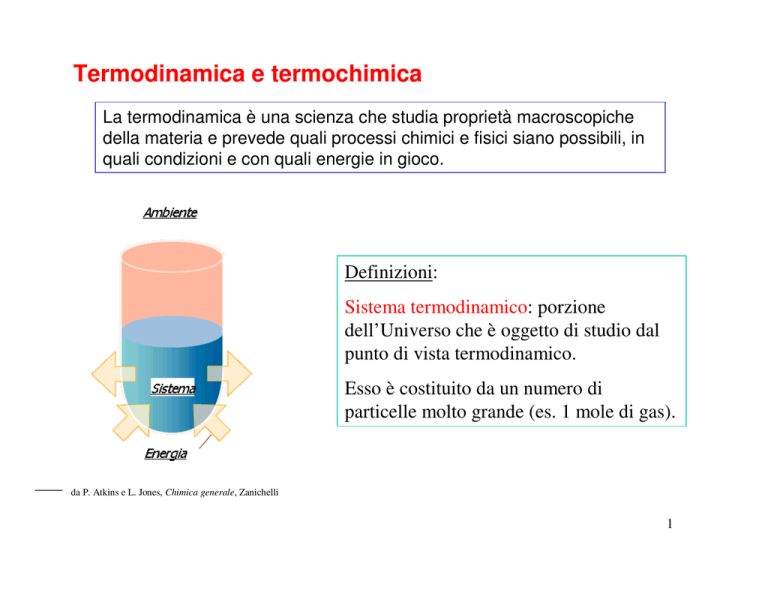
Definizioni:
Sistema termodinamico: porzione
dell’Universo che è oggetto di studio dal
punto di vista termodinamico.
Esso è costituito da un numero di
particelle molto grande (es. 1 mole di gas).
da P. Atkins e L. Jones, Chimica generale, Zanichelli
1
Un sistema può essere aperto: scambia con l’ambiente sia energia sia materia
chiuso: scambia con l’ambiente solo energia e non materia
isolato: non scambia con l’ambiente né energia né materia
Aperto
Chiuso
Isolato
da P. Atkins e L. Jones, Chimica generale, Zanichelli
2
Possiamo descrivere un sistema termodinamico attraverso la
misurazione di alcune proprietà macroscopiche, che dipendono
dallo stato in cui si trova il sistema.
Queste proprietà si chiamano variabili (o grandezze) di stato.
Temperatura è la manifestazione macroscopica dell’energia cinetica
media delle molecole di un gas;
Pressione è la manifestazione macroscopica degli urti tra le molecole
di un gas e le pareti del recipiente.
Lo stato di un sistema termodinamico
Si può dire che un sistema si trova in EQUILIBRIO
TERMODINAMICO quando i valori di tutte le variabili che lo
descrivono NON cambiano nel tempo.
Viceversa, se i valori cambiano nel tempo, il sistema subisce una
3
TRASFORMAZIONE DI STATO.
L’energia contenuta all’interno del sistema termodinamico è detta
energia interna (E).
Durante una trasformazione di stato in sistemi aperti e chiusi ci
possono essere trasferimenti di energia.
I trasferimenti di energia tra un sistema ed il suo intorno possono
avvenire sotto forma di calore (Q) o di lavoro (W).
Q e W sono mezzi differenti mediante i quali una quantità di
energia può essere scambiata.
Q
W
Sistema chiuso
∆E>0
Q
W
Sistema chiuso
∆E<0
4
Per un gas reale vanno considerate anche
le interazioni intermolecolari e quindi
l’energia di interazione (Einter) ad esse
associate
H
F
Ek(elettronica)
E = E elettr + E trasl + E rot + E vibr
5
Calore = rappresenta l’energia trasferita in seguito ad una
differenza di temperatura
Lavoro = viene preso in considerazione solo il lavoro meccanico
coinvolto nella compressione ed espansione di un gas.
Pressione esercitata dal
peso m sul pistone
Esiste una convenzione che stabilisce
quando lavoro e calore hanno segni
positivi e negativi
P = F/A
F =P.A
L = F·h = P·A ·h = P ·∆V
6
Energia interna
Altezza
L’energia interna è una FUNZIONE DI STATO:
durante una trasformazione il valore di E non dipende
dal percorso seguito, ma solo dallo stato INIZIALE e
dal quello FINALE.
∆E
da P. Atkins e L. Jones, Chimica generale, Zanichelli
Il lavoro e il calore non sono FUNZIONI DI STATO. I valori di
Q e W dipendono da come avviene la trasformazione.
7
1° PRINCIPIO
In un sistema chiuso ogni variazione di energia interna,
in seguito ad una trasformazione termodinamica, è
uguale all’energia, di qualunque tipo, che il sistema
cede o riceve dall’ambiente; se il sistema è isolato la
sua energia rimane costante.
∆E = Q + W = Q - P∆
∆V
Per il 1° principio della termodinamica:
- in trasformazioni a volume costante: ∆V=0 e ∆E = QV
-in trasformazioni a pressione costante:
P∆
∆V = ∆(PV)
QP = ∆E + ∆PV = ∆(E + PV) = ∆H
H = (E+PV) entalpia
8
Termochimica
La termochimica si occupa dell’effetto termico associato alle reazioni
chimiche.
aA + bB + ....... → lL + mM + ......
Ei = energia interna molare
Hi= entalpia molare
Q P = ∆H = (lH L + mH M + .......) − (aH A + bH B + .......) = ∑ν i H i
QV = ∆E = (lE L + mE M + .......) − (aE A + bE B + .......) = ∑ν i E i
9
Sperimentalmente si verifica che il calore svolto o assorbito in una
reazione chimica dipende dallo stato iniziale e finale del sistema,
dalla massa e dallo stato di aggregazione dei reagenti e dei prodotti e
dalle condizioni di trasformazione.
Le reazioni possono essere condotte in condizioni sperimentali
diverse, ad esempio:
a T e V costanti (in un reattore a volume costante)
a T e P costanti (in un reattore mantenuto a P = 1 atm)
La maggior parte delle reazioni chimiche è condotta a T e P costanti,
per cui il calore ad esse associato è rappresentato dalla variazione di
entalpia ∆H.
La determinazione sperimentale dei calori di reazione è condotta in
apparecchiature opportune chiamate calorimetri.
10
11
Equivalenza tra calore ed energia meccanica
Nelle reciproche trasformazioni di lavoro in calore e viceversa, vi è un rapporto
costante, J, tra lavoro speso e calore prodotto:
W / Q = J = 4,1840
J viene detto “equivalente meccanico della caloria” e, esprimendo W in joule e Q in
calorie, risulta uguale a 4,1840.
12
Equazioni termochimiche
Quando in una equazione stechiometrica compare il calore svolto o assorbito dalla
reazione si parla di equazione termochimica:
C(s, gr) + O2 (g) CO2 (g)
∆H(25°C, 1 atm) = - 394,0 KJ
Occorre specificare:
l’unità di misura con cui è espresso il calore;
il numero di moli di tutte le sostanze;
lo stato di aggregazione di ogni sostanza;
la temperatura e la pressione a cui la reazione è condotta.
Per uniformare i dati calorimetrici è necessario stabilire uno stato di riferimento detto
stato standard:
Gas:
gas ideale alla pressione di 1 atm
Liquidi: liquido puro alla pressione di 1 atm
Solidi: solido puro alla pressione di 1 atm. Se il solido presenta più forme cristalline,
si considera la forma cristallina stabile alla temperatura considerata e a P= 1 atm
Soluto: soluzione ideale a concentrazione 1 molare
La temperatura non compare nella definizione di stato standard; in genere, i dati sono
tabulati alla temperatura di 25°C. Quando ci si riferisce allo stato standard si scrive
13
H° o ∆H°.
Entalpia Standard di Reazione ( ∆H°reaz)
Si definisce entalpia standard di reazione l’effetto termico che accompagna la
reazione quando sia i prodotti sia i reagenti si trovano nel loro stato standard e
reagiscono secondo i rapporti molari indicati nell’equazione, a T e P costanti.
I valori della variazione di entalpia standard di una reazione sono solitamente
riportati a 25°C.
H2 (g) + ½ O2 (g) H2O(g)
∆H°(25°C) = - 242,0 KJ
Le reazioni esotermiche, caratterizzate da sviluppo di calore, presentano
∆H°<0
Le reazioni endotermiche, caratterizzate da assorbimento di calore, presentano
∆H°>0
14
Calcolo delle entalpie di reazione
Per il calcolo dell’entalpia di reazione (calore di reazione a pressione
costante) i dati essenziali sono le entalpie molari delle singole specie
chimiche partecipanti alla reazione:
QP = ∆H = (lH L + mHM + .......) − (aH A + bHB + .......) = ∑ν i H i
QV =Le
∆Eentalpie
= (lE L +
mEMdelle
+ .......)
− (aEAvengono
+ bEB +determinate
.......) = ∑ν i Ei
molari
sostanze
facendo riferimento alle reazioni di formazione delle sostanze
stesse, ponendo uguale a zero l’entalpia molare degli elementi
15
Entalpia Molare Standard di Formazione (∆
∆H°f)
Si definisce reazione di formazione di un composto la reazione in cui una mole del
composto considerato si forma dagli elementi costituenti.
La variazione di entalpia molare standard di formazione rappresenta la variazione
di entalpia della reazione di formazione condotta in condizioni standard.
½ H2 (g) + ½ Cl2 (g) 1 HCl(g)
∆H°f, HCl(g) = - 92,3 KJ/mol
Convenzionalmente è stato assegnato valore zero all’entalpia molare
standard degli elementi nel loro stato standard (H°fel = 0) :
∆H°f, HCl
(g)
= H° HCl – ( ½ H° H
(g)
2 (g)
+ ½ H° Cl
2 (g)
) = - 92,3 KJ/mol = H° HCl(g)
I ∆H°f (e quindi gli H°) sono misurabili direttamente solo per poche reazioni perché
solo per poche sostanze è possibile condurre sperimentalmente una reazione di
formazione “pulita”.
16
17
Entalpia Molare Standard di Combustione ( ∆H°comb)
Si definisce reazione di combustione la reazione tra una mole di un elemento o di un
composto e ossigeno. In genere si ha la formazione di CO2 e H2O (per sostanze
contenenti H e C). Poiché l’acqua può essere allo stato liquido o di vapore, occorre
specificare se ci si riferisce ad un caso o all’altro.
La variazione di entalpia molare standard di combustione rappresenta la variazione
di entalpia della reazione di combustione condotta in condizioni standard.
CH4 (g) + 2 O2 (g) CO2 (g) + 2 H2O (g)
∆H°comb = - 191,8 Kcal/mol
CH4 (g) + 2 O2 (g) CO2 (g) + 2 H2O (l)
∆H°comb = - 212,8 Kcal/mol
18
Legge di Hess
“In una reazione chimica l’effetto termico a pressione costante è
indipendente dagli stati intermedi attraverso i quali la reazione passa
(o si immagina che passi), ma dipende solo dagli stati iniziali e da
quelli finali”
∆HI-F
I
F
∆HI-A
∆HB-F
A
∆HA-B
B
∆HI-F = ∆HI-A + ∆HA-B + ∆HB-F19
Consideriamo la reazione di formazione dell’etene C2H4 (g) a 25°C:
2 C(s, gr) + 2 H2 (g)
C2H4 (g)
∆H°f, C2H4 (g) = ?
Non è possibile ottenere sperimentalmente il valore di ∆H°f, C2H4 (g), perché in qualunque
condizione si operi si ottiene sempre una miscela di prodotti.
Occorre dedurre ∆H°f, C2H4 (g) in modo indiretto. Consideriamo i seguenti dati:
∆H°comb, C2H4 (g) = - 337,2 Kcal/mol
∆H°f, CO2 (g) = - 94,1 Kcal/mol
∆H°f, H2O (l) = - 68,3 Kcal/mol
∆H°X
2 C (s,gr)
∆H°I
+ 2 O2(g)
2 CO2 (g)
∆H°X + ∆H°III = ∆H°I + ∆H°II ;
+
2 H2 (g)
∆H°II + O2 (g)
+
C2H4 (g)
∆H°III
+ 3 O2 (g)
2 H2O (l)
∆H°X = ∆H°I + ∆H°II - ∆H°III
dove ∆H°I=2·∆H°f,CO2(g) ; ∆H°II= 2·∆H°f,H2O(l) ;
∆H°III=∆H°comb,C2H4(g)
∆H°f,C2H4(g)= 2·∆H°f,CO2(g)+ 2·∆H°f,H2O(l) - ∆H°comb,C2H4(g)= 2·(-94,1)+2·(-68,3)–(-337,2)=12,4 Kcal/mol
20
Esercizi
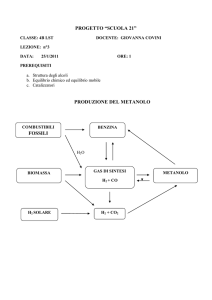
1. Calcolare l’entalpia standard di formazione a 25°C dell’alcol metilico (CH3OH) liquido
conoscendo i seguenti dati alla stessa temperatura:
∆H°comb, CH3OH (l) = -728 KJ/mol; ∆H°f, CO2(g) = - 394 KJ/mol;
∆H°f, H2O(l) = - 286 KJ/mol
Soluzione: Si scrive la reazione, bilanciata, di cui si vuole calcolare l’effetto termico e si imposta
un ciclo utilizzando le reazioni di cui si conoscono gli effetti termici:
∆H°X
C (s,gr) + 1/2 O2 (g) + 2 H2 (g)
∆H°I + 1/2 O2(g)
CO2 (g)
Per la legge di Hess:
dove:
∆H°II + O2 (g)
+
CH3OH (l)
∆H°III + 3/2 O2 (g)
2 H2O (l)
∆H°X + ∆H°III = ∆H°I + ∆H°II ;
∆H°X = ∆H°I + ∆H°II - ∆H°III
∆H°I = ∆H°f, CO2 (g)
∆H°II = 2 · ∆H°f, H2O(l)
∆H°III = ∆H°comb, CH3OH (l)
Sostituendo:
∆H°f, CH3OH (l) = ∆H°f, CO2 (g) + 2 ·∆H°f, H2O(l) - ∆H°comb, C2H6 (g) = -238 Kcal/mol
21
2. Calcolare l’entalpia standard di formazione a 25°C dell’etano (C2H6) gassoso conoscendo i
seguenti dati alla stessa temperatura:
∆H°comb, C2H6 (g) = -373 Kcal/mol; ∆H°f, CO2 (g) = - 94,1 Kcal/mol;
∆H°f, H2O(l) = - 68,3 Kcal/mol
Soluzione: Si scrive la reazione, bilanciata, di cui si vuole calcolare l’effetto termico:
2 C (s,gr) + 3 H2 (g) C2H6 (g)
Si imposta un ciclo utilizzando le reazioni di cui si conoscono gli effetti termici:
2 C (s,gr) + 3 H2 (g)
∆H°X
∆H°I + 2 O2 ∆H° + 3/2 O2
II
C2H6 (g)
+ 7/2 O2
∆H°III
2 CO2 (g) + 3 H2O (l)
Per la legge di Hess:
dove:
∆H°X + ∆H°III = ∆H°I + ∆H°II ;
∆H°X = ∆H°I + ∆H°II - ∆H°III
∆H°I = 2· ∆H°f, CO2 (g)
∆H°II = 3 · ∆H°f, H2O(l)
∆H°III = ∆H°comb, C2H6 (g)
Sostituendo:
∆H°f, C2H6 (g) = 2· ∆H°f, CO2 (g) + 3 ·∆H°f, H2O(l) - ∆H°comb, C2H6 (g) = -188,2 – 204,9 + 373 = - 20,1
22
Kcal/mol
3. Calcolare il calore di combustione a 25°C dell’alcool metilico liquido CH3OH(l), dai seguenti dati
alla stessa temperatura:
∆H°f, CO2 (g) = - 94.1 Kcal/mol;
∆H°f, H2O (l) = - 68.3 Kcal/mol; ∆H°f, CH3OH (l) = -56.9 Kcal/mol;
Soluzione: Si scrive la reazione, bilanciata, di cui si vuole calcolare l’effetto termico e si imposta
un ciclo utilizzando le reazioni di cui si conoscono gli effetti termici:
CH3OH (l) + 3/2 O2 (g)
∆H°I
+ 1/2 O2(g)
∆H°X
CO2 (g) +
∆H°II + O2 (g)
2 H2O (l)
∆H°III
C (s,gr) +
Per la legge di Hess:
dove:
∆H°X + ∆H°I = ∆H°I I + ∆H°III ;
+ O2 (g)
2 H2 (g)
∆H°X = ∆H°II – ∆H°III - ∆H°I
∆H°I = ∆H°f, CH3OH (l)
∆H°II = ∆H°f, CO2 (g)
∆H°III = 2 ·∆H°f, H2O (l)
Sostituendo:
∆H°comb, CH3OH (l)=∆H°f, CO2(g)+2 ·∆H°f, H2O(l) -∆H° f, CH3OH(l) = -94,1+2·(-68,3)+ 56,9 = -174 Kcal/mol
23
4. Calcolare l’energia del legame C-H attraverso la valutazione della variazione di entalpia della
reazione:
C(g) + 4 H(g) → CH4 (g)
conoscendo i seguenti dati:
C(s,gr) + 2 H2 (g) → CH4 (g)
∆H°f, CH4 (g) = - 74.81 kJ/mol
C(s,gr) → C (g)
∆H°subl, C (s,gr) = 712.96 kJ/mol
H2 (g) → 2 H (g)
∆H°dissoc, H2 (g) = 435.94 kJ/mol
Soluzione: Si scrive la reazione, bilanciata, di cui si vuole calcolare l’effetto termico e si imposta
un ciclo utilizzando le reazioni di cui si conoscono gli effetti termici:
∆H°X
C (g) +
∆H°I
4 H (g)
∆H°II
CH4 (g)
∆H°III
C (s,gr) + 2 H2 (g)
Per la legge di Hess:
dove:
∆H°I + ∆H°I I + ∆H°X = ∆H°III ;
∆H°X = ∆H°III – ∆H°I - ∆H°II
∆H°I = ∆H°subl, C (s,gr)
∆H°II = 2 · ∆H°dissoc, H2 (g)
∆H°III = ∆H°f, CH4 (g)
Sostituendo:
∆H°reaz= ∆H°f, CH4 (g) - ∆H°subl, C (s,gr) - 2 · ∆H°dissoc, H2 (g) = -74,81-712,96-(2 · 435,94) = -1667 KJ/mol
24
Per un legame C-H: 1667/4 = 416.9 kJ/mol. Quindi, l’energia di legame media C-H è 417 kJ/mol