Risoluzione di equazioni non lineari

Risoluzione di equazioni non lineari
Si considera il problema di determinare la soluzione dell’equazione
f (x) = 0
ove f (x) è una funzione definita in un intervallo [a, b], chiuso e
limitato. Ogni valore x∗ ∈ [a, b] per cui f (x∗) = 0 si dice RADICE
dell’equazione f (x) = 0 oppure ZERO della funzione f (x). Se non si
hanno a disposizione strumenti analitici, il grafico di f (x) nell’intervallo
considerato può fornire in modo rapido una approssimazione della
soluzione cercata. Risulta tuttavia preferibile disporre di metodi
numerici in grado di fornire soluzioni con una accuratezza prefissata.
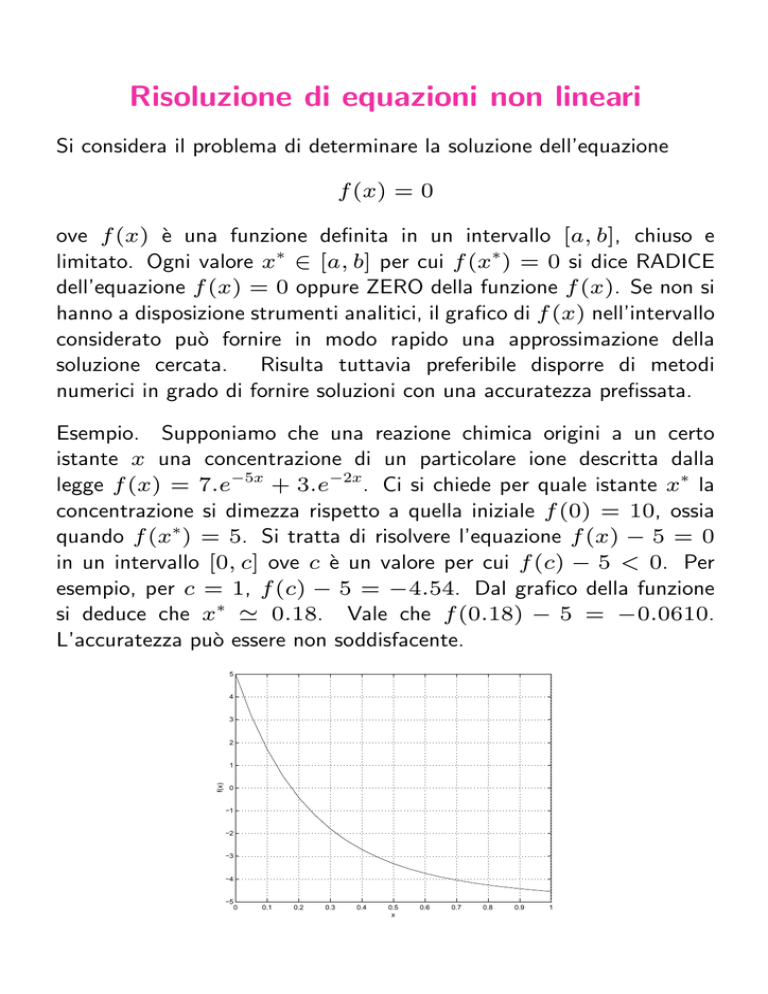
Esempio. Supponiamo che una reazione chimica origini a un certo
istante x una concentrazione di un particolare ione descritta dalla
legge f (x) = 7.e−5x + 3.e−2x. Ci si chiede per quale istante x∗ la
concentrazione si dimezza rispetto a quella iniziale f (0) = 10, ossia
quando f (x∗) = 5. Si tratta di risolvere l’equazione f (x) − 5 = 0
in un intervallo [0, c] ove c è un valore per cui f (c) − 5 < 0. Per
esempio, per c = 1, f (c) − 5 = −4.54. Dal grafico della funzione
si deduce che x∗ ' 0.18. Vale che f (0.18) − 5 = −0.0610.
L’accuratezza può essere non soddisfacente.
5
4
3
2
f(x)
1
0
−1
−2
−3
−4
−5
0
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9
1
Metodo di bisezione
La tecnica più semplice per determinare lo zero di una funzione continua
in [a, b] che assume segno opposto agli estremi dell’intervallo, consiste
nella dimostrazione costruttiva del seguente teorema (è un corollario del
Teorema del valor medio).
Teorema degli zeri di una funzione continua. Sia f (x) una funzione
continua in [a, b] chiuso e limitato e sia f (a).f (b) < 0. Allora esiste
un punto x∗ ∈ (a, b) tale che f (x∗) = 0.
Per determinare x∗ si costruisce una successione di intervalli
I1 = [a1, b1], I2 = [a2, b2], ..., Ik = [ak , bk ]
tali che
Ik ⊂ Ik−1 ⊂ Ik−2 ⊂ ... ⊂ I1
con f (ak ).f (bk ) < 0, k = 1, 2, .... E’ a1 = a, b1 = b.
La costruzione degli intervalli avviene nel seguente modo. Si pone
a1 = a, b1 = b. Sia f (a1) < 0 e f (b1) > 0 (in caso contrario si
determinano le radici di −f (x) = 0).
Al passo k si calcola
ck =
ak + bk
2
k = 1, 2, ...
e il valore f (ck ).
Se f (ck ) = 0, ck = x∗.
Altrimenti si pone:
½
[ak+1, bk+1] =
[ak , ck ]
[ck , bk ]
se f (ck ) > 0
se f (ck ) < 0
Pertanto è f (ak+1) < 0, f (bk+1) > 0 e Ik+1 ⊂ Ik .
bk+1 − ak+1 =
1
1
1
(bk − ak ) = 2 (bk−1 − ak−1) = ... = k (b1 − a1)
2
2
2
Allora in Ik+1 giace x∗ che è la radice di f (x) = 0 e x∗ = ck+1 ±²k+1,
ove
1
²k+1 ≤ k+1 (b − a)
2
1
Pertanto, fissata ² tale che ² = k+1
(b − a), il numero ck+1 è una
2
∗
approssimazione di x entro una tolleranza ². Col metodo di bisezione
è possibile determinare una successione di approssimazioni di x∗ tali
che
1
∗
|ck − x | ≤ k (b − a)
k≥1
2
Per k → ∞, {ck } converge a x∗ con velocità di convergenza pari a
quella della successione { 1k }. Il metodo fornisce un valore maggiorante
2
dell’errore. Da tale valore è possibile determinare il minimo numero di
iterazioni k necessarie ad ottenere un errore assoluto che non supera
una tolleranza ² prefissata. Infatti k è tale che
1
(b − a) ≤ ²
2k
log10 b−a
b−a
b−a
²
⇒2 ≥
⇒ k ≥ log2
=
²
²
log102
Occorrono allora almeno k + 2 valutazioni di funzione (1 per ogni
iterazione +2 per il passo iniziale).
k
Esempio. Si vuole risolvere x2 − 78.8 = 0 in [6, 12].
k
1
2
3
4
5
6
7
8
ak
6
6
7.5
8.25
8.625
8.8125
8.8125
8.859375
f (6)
=
36 − 78.8 < 0
f (12)
=
144 − 78.8 > 0
bk
12
9
9
9
9
9
8.90625
8.90625
ck
9
7.5
8.25
8.625
8.8125
8.90625
8.859375
8.882813
8.882813 è una approssimazione
8.876936408 tale che
∗
|8.882813 − x | ≤
f (ck )
2.2
-22.55
-10.7375
-4.409375
-1.139844
0.5212891
-0.3114746
0.1043579
della
soluzione
√
78.8
'
1
6 = 0.0234
28
L’errore assoluto è 0.00587... Occorrono 10 valutazioni di funzione.
Esempio. Determinare il numero di iterazioni necessarie a risolvere
x3 + 4x2 − 10 = 0 con una tolleranza ² = 10−5 in [1, 2].
Deve essere
1
−5
(b
−
a)
≤
10
2k
b−a
k
5
2 ≥
⇒
k
≥
log
10
' 16.6
2
10−5
Allora deve essere k almeno uguale a 17. Occorrono 17 + 2 valutazioni
di funzioni.
Osservazioni
• Se a e b sono valori molto vicini, operando con aritmetica finita,
il calcolo di c con la formula a+b
2 può fornire un numero esterno
a [a, b]. Conviene calcolare il punto medio con la formula c =
a + b−a
2 . Per esempio, se a = 0.983, b = 0.986, lavorando in
artimetica finita con tre cifre di precisione decimale, si ha:
f l(a + b)
a+b
f l(
)
2
1
=
f l(0.983 + 0.986) = .196 10 troncamento
=
.196 101
f l(
) = .980
2
che è esterno all’intervallo [.983, .986].
f l(b − a)
b−a
f l(
)
2
b−a
f l(a +
)
2
=
f l(0.986 − 0.983) = .3 10
=
.3 10−2
−2
f l(
) = .150 10
2
=
f l(.983 + .150 10
−2
−2
) = f l(.983 + .0015) =
che è interno all’intervallo [.983, .986].
• Pur essendo f (a) e f (b) rappresentabili sulla macchina, può
essere che il loro prodotto, calcolato per verificare il segno, non
sia rappresentabile sulla macchina. E’ preferibile allora usare la
funzione sign(x) per esaminare il segno di f (a) e di f (b), ove

x>0
 1
sign(x) =
0
x=0

−1 x < 0
• L’algoritmo di bisezione realizzato in aritmetica finita può non avere
fine. Se ak = 98.5 e bk = 98.6 e ² = 0.004 in aritmetica
con tre cifre decimali di precisione, il test bk − ak < ² non è
b −a
verificato. Ma ck = ak + k 2 k = 98.5 + 0.1/2 = 98.55, ma
f l(98.55) = 98.5. Si genera una successione di iterati costanti.
Occorre dunque usare il test
|bk − ak | < ² + eps.max(|b|, |a|)
(in modo che si eliminano inconvenienti dovuti al fatto di scegliere
una tolleranza troppo piccola, inferiore relativamente rispetto alla
precisione di macchina) e prevedere un massimo numero di iterazioni.
Il metodo di bisezione ha la caratteristica positiva di convergere a uno
zero di f (x) nella sola ipotesi di f (x) continua con segno opposto agli
estremi. Tuttavia la convergenza è lenta (si guadagna una cifra decimale
ogni 3 iterazioni circa se b − a = 1 ). Pertanto spesso viene usato
solo per individuare l’intervallo entro cui cade lo zero di una funzione
come tecnica di approssimazione iniziale. Una volta individuato tale
intervallo (entro cui in genere valgono ipotesi più forti), si raggiungono
approssimazioni migliori con metodi a convergenza più veloce.
Metodo delle approssimazioni successive
Il problema di determinare lo zero di una funzione in genere non si risolve
in un numero finito di passi. Si tratta di generare un procedimento
iterativo. Esso comporta:
• determinazione di una approssimazione iniziale alla soluzione x∗ di
f (x) = 0;
• determinare una relazione funzionale a partire da f (x);
• a partire da x0, generare, valutando la relazione funzionale
determinata, una successione di iterati xk fino ad ottenere la
precisione desiderata o fino a che si raggiunge un massimo numero
di iterazioni.
Occorre poi determinare le condizioni per cui {xk } converge per k →
∞.
Se {xk } converge per ogni x0 ∈ [a, b] si parla di convergenza globale;
se invece si ha convergenza solo per gli x0 appartenenti a un opportuno
intervallo che contiene x∗, allora si parla di convergenza locale.
Il problema di cercare la radice di f (x) = 0 è strettamente connesso
al problema di determinare la soluzione dell’equazione
x = g(x)
ossia il valore x∗ per cui x∗ = g(x∗). x∗ si dice punto fisso di g(x).
Infatti, data f (x) = 0 in [a, b], sia φ(x) una funzione che non si
annulla ed è limitata in [a, b]:
0 < |φ(x)| < ∞
x ∈ [a, b]
Preso g(x) = x − φ(x)f (x), il problema
f (x) = 0
x ∈ [a, b]
è equivalente a trovare le soluzioni di
x = g(x)
x ∈ [a, b]
Se infatti x∗ è punto fisso di g(x), ossia x∗ = g(x∗), si ha che
x∗ − g(x∗)
f (x ) =
=0
φ(x∗)
∗
∗
φ(x ) 6= 0
Viceversa se f (x∗) = 0, allora
∗
∗
∗
∗
g(x ) = x − φ(x )f (x ) = x
∗
Pertanto si riporta il problema di determinare lo zero di f (x) in [a, b] a
quello di individuare il punto fisso di g(x) in [a, b]. Geometricamente
questo significa calcolare l’intersezione tra la retta y = x (bisettrice
del I e III quadrante) e la funzione y = g(x). Una possibile scelta di
φ(x) è φ(x) = ±1.
1.5
1
0.5
0
−0.5
0
0.5
1
1.5
Teorema. Sia g(x) continua in [a, b] e tale che g(x) ∈ [a, b]. Sia L
una costante 0 ≤ L < 1 tale che, per ogni x, y ∈ [a, b], vale che
|g(x) − g(y)| ≤ L|x − y|
(ossia g(x) è una contrazione in [a, b]). Allora esiste un unico punto
fisso x∗ di g(x) in [a, b].
Dimostrazione. (Esistenza). Sia h(x) = x − g(x). Poichè g(x) ∈ [a, b], g(a) ≥ a e g(b) ≤ b.
Se g(a) = a o g(b) = b, allora si è già trovato il punto fisso. In caso contrario, è g(a) > a e
g(b) < b. Dunque,
h(a) = a − g(a) < 0
h(b) = b − g(b) > 0
e poichè h(x) è continua, per il teorema degli zeri di una funzione continua, esiste x∗ ∈ (a, b) tale
che h(x∗ ) = 0 e dunque x∗ = g(x∗ ).
(Unicità). Supponiamo che ci siano due punti fissi x∗ e y ∗ in [a, b]. Allora, se x∗ =
6 y ∗ , segue
∗
∗
∗
∗
∗
∗
∗
∗
|x − y | = |g(x ) − g(y )| ≤ L|x − y | < |x − y |
Ciò è assurdo ¤.
Se g(x) è derivabile in [a, b] con |g 0(x)| ≤ L < 1 per x ∈ [a, b],
allora g(x) è una contrazione. Infatti per il teorema di Lagrange, esiste
ξ ∈ [a, b], tale che
g(x) − g(y)
0
= g (ξ) x < ξ < y
x−y
Allora
0
|g(x) − g(y)| = |g (ξ)||x − y| ≤ L|x − y|
Il viceversa non è vero poichè g(x) può non essere differenziabile.
4
3.5
g(x)
b
3
2.5
2
1.5
a
1
0.5
b
a
0
0
0.5
1
1.5
2
2.5
3
3.5
4
Occorre g(x) ∈ [a, b]
4
3.5
b
3
g(x)
2.5
2
1.5
a
1
0.5
b
a
0
0
0.5
1
1.5
2
2.5
3
3.5
4
Occorre g(x) continua perchè ci sia un punto fisso
4
3.5
b
3
g(x)
2.5
2
1.5
a
1
0.5
b
a
0
0
0.5
1
1.5
2
2.5
3
3.5
4
Occorre che g(x) non oscilli troppo, ossia che sia una contrazione,
perchè ci sia un unico punto fisso.
Esempi.
1. g(x) = x in [0, 1] ha infiniti punti fissi. x è continua in [0, 1] e
x ∈ [0, 1]. Ma g 0(x) = 1 per x ∈ [0, 1].
2. g(x) = x − sin(πx) in [0, 1] ha due punti fissi x = 0 e x = 1.
g(x) è continua in [0, 1]. Ma g(x) non appartiene a [0, 1]
(g(1/2) = −1/2).
3. g(x) = (x2 −1)/3 in [−1, 1]. g(x) è continua e g(x) ∈ [−1, 1].
Inoltre g 0(x) = 32 x e |g 0(x)| ≤ 23 per x ∈ [−1, 1]. Dunque esiste
2
un unico punto fisso in√ [−1, 1]. Esso è x 3−1 = x ⇒ x2 −3x−1 =
∗
3− 13
0. Perciò
x
=
. In [3, 4], g(x) ha un altro punto fisso
2
√
x∗ = 3+2 13 . Ma g(x) non appartiene a [3, 4] e g 0(4) = 8/3 > 1.
Qui non sono soddisfatte le ipotesi del teorema. Infatti queste sono
solo condizioni sufficienti.
Data una approssimazione iniziale x0 di x∗, punto fisso di g(x) in
[a, b], si genera una successione di iterati mediante il metodo delle
approssimazioni successive o del punto fisso o iterazione funzionale:
xk+1 = g(xk )
Se g(x) è continua e la successione {xk } degli iterati è convergente
per k → ∞ a un punto x∗, allora x∗ è punto fisso fi g(x). Infatti
∗
∗
x = lim xk+1 = lim g(xk ) = g(lim xk ) = g(x )
k→∞
k→∞
k→
Dal punto di vista geometrico, il metodo dell’iterazione funzionale
equivale alla costruzione di una poligonale con lati orizzontali e verticali
orientata nel piano xy . Le figure seguenti aiutano a individuare le
condizioni da imporre a g(x) perchè i vertici della poligonale convergano
a (x∗, g(x∗)).
4
3.5
b
3
g(x)
2.5
2
1.5
a
1
0.5
0
0.5
1
1.5
x0
x1
x2
a
0
2
2.5
b
3
3.5
4
Convergenza monotona:
{xk } converge a x∗ approssimando sempre per eccesso o per difetto.
4
3.5
b
3
g(x)
2.5
2
1.5
a
1
0.5
a
0
0
0.5
1
x0
1.5
x2
2
x3
2.5
x1
b
3
3.5
4
Convergenza alternata:
{xk } converge a x∗ approssimando per eccesso e per difetto.
4
3.5
g(x)
b
3
2.5
2
1.5
a
1
0.5
a
0
0
0.5
1
b
1.5
2
2.5
3
2
2.5
3
3.5
4
3.5
4
g 0 (x) > 1
4
3.5
g(x)
b
3
2.5
2
1.5
a
1
0.5
a
0
0
0.5
1
g 0 (x) < −1
b
1.5
Per |g 0 (x)| > 1 non c’è convergenza.
Teorema di convergenza globale del metodo
delle approssimazioni successive
Sia g(x) una funzione definita in un intervallo [a, b]chiuso e limitato.
Sia:
• g(x) continua in [a, b];
• g(x) ∈ [a, b];
• g(x) sia una contrazione in [a, b].
Allora per ogni x0 ∈ [a, b], la successione delle approssimazioni
successive {xk } con xk = g(xk−1), k = 1, 2, ..., converge per
k → ∞ all’unico punto fisso x∗ di g(x) in [a, b].
Dimostrazione. Le ipotesi garantiscono l’esistenza e l’unicità di un unico punto fisso x∗ della funzione
g(x) in [a, b]. Poichè inoltre xk = g(xk−1 ), allora per ogni successione generata a partire da un
punto x0 ∈ [a, b], l’iterato xk è ben definito, ossia xk ∈ [a, b], poichè g(xk−1 ) ∈ [a, b].
Si consideri:
∗
|xk − x |
=
∗
∗
|g(xk−1 ) − g(x )| ≤ L|xk−1 − x | =
=
∗
2
∗
L|g(xk−2 ) − g(x )| ≤ L |xk−2 − x |...
≤
k
∗
L |x0 − x |
Poichè 0 < L < 1, per k → ∞ si ha limk→∞ Lk = 0 e dunque limk→∞ xk = x∗ .
Si può trovare una maggiorazione dell’errore, osservando che:
∗
∗
∗
|x0 − x | = |x0 − x1 + x1 − x | ≤ |x0 − x1 | + L|x0 − x |
Da ciò |x0 − x∗ | ≤ 1 |x1 − x0 |. Allora
1−L
Lk
∗
|xk − x | ≤
|x − x0 |
1−L 1
La velocità di convergenga dipende da L. Quanto più L è vicino a 1
quanto più la convergenza è lenta e viceversa.
Esempio. Si considerano vari modi di innescare un procedimento
iterativo di punto fisso per poter trovare la soluzione della funzione
3
2
x + 4x − 10 = 0
in [1, 2]
. Si considera come punto iniziale in tutti i casi x0 = 1.5.
(a). x = x − x3 − 4x2 + 10 = g1(x);
¢1/2
¡ 10
= g2(x) (da x3 = 10 − 4x2));
(b). x = x − 4x
(c). x = 12 (10 − x3)1/2 = g3(x) (da x2 = 14 (10 − x3));
´1/2
³
10
(d). x = x+4
= g4(x) (da x3 + 4x2 = 10);
(e). x = x −
k
1
2
(a)
-0.875
6.732
3
4
...
15
...
30
-469.7
1.08 108
diverge
x3 +4x2 −10
3x2 +8x
(b)
0.8165
2.9969
(−8.65)1/2
impossibile
= g5(x) (da x = x −
f (x)
).
f 0 (x)
(c)
1.286953768
1.402540804
(d)
1.348399725
1.367376372
(e)
1.373333333
1.365262015
1.345458374
1.375170253
...
1.365223680
...
1.365230013
1.364957015
1.365264748
...
1.365230013
1.365230014
1.365230013
Non tutte le scelte portano a un metodo convergente (caso (a)) o ben
definito (caso (b)). Tuttavia anche se il metodo è convergente, ci
sono funzioni che portano a una più rapida convergenza di altre (con il
metodo di bisezione sono necessarie 27 valutazioni di funzioni).
(a). g10 (x) = 1 − 3x2 − 8x, |g10 (x)| > 1 per x ∈ [1, 2];
√
√
(b). g2(x) è definita per − 10/2 ≤ x ≤ 10/2 ' 1.581113;
dunque g2(x) non appartiene a [1, 2];
(c).
g30 (x) = − 34
x2
;
(10−x3 )1/2
dunque |g30 (x)| ≤ 2.1213.
Tuttavia se ci si restringe a [1, 1.5], 1.28 ≤ g3(x) ≤ 1.5 e
max[1,1.5]|g30 (x)| = |g30 (1.5)| ' 0.6556 < 1;
q
0
x+4
(x)| ≤ 0.15; la convergenza è più
(d).
=
,
per
cui
|g
4
10
rapida che nel caso (c);
g40 (x)
1
2
4
3
2
−60x−80
(e). g50 (x) = 6x +32x(3x+32x
; in [1, 2], |g50 (x)| ≤ 0.6.
2 +8x)2
Tuttavia g5(x) è il metodo a convergenza più rapida. Ciò dipende
dal fatto che in [1, 1.5], |g50 (x)| ≤ 0.11. Invece |g40 (x)| ≤ 0.123.
Da ciò segue la più veloce convergenza del caso (e) rispetto a (d).
Spesso è difficile verificare la condizione: per x ∈ [a, b], g(x) ∈ [a, b]
che è essenziale nel teorema di convergenza globale; in tal caso è utile
un teorema di convergenza locale che assicura la convergenza di {xk }
a un punto fisso x∗ di g(x) se x0 è sufficientemente vicino a x∗. E’
necessario sapere a priori che x∗ è un punto fisso di g(x), ossia che
g(x) ha un punto fisso.
Teorema di convergenza locale. Sia x∗ un punto fisso di g(x);
si suppone che g(x) sia continua e sia una contrazione per ogni
x ∈ [x∗ − ρ, x∗ + ρ] = Iρ. Allora, per ogni x0 ∈ Iρ, la successione
degli {xk } è ben definita, ossia xk ∈ Iρ e converge per k → ∞ a x∗.
Inoltre x∗ è l’unico punto fisso di g(x) in Iρ.
Dimostrazione. Per ipotesi x0 ∈ Iρ e dunque
∗
|x0 − x | ≤ ρ
Preso g(x0 ) = x1 ,
∗
∗
∗
|x1 − x | = |g(x0 ) − g(x )| ≤ L|x0 − x | ≤ Lρ < ρ
poichè L < 1. Supposto ora che x2 , ..., xk ∈ Iρ , si dimostra che ciò vale anche per xk+1 :
∗
∗
∗
|xk+1 − x | = |g(xk ) − g(x )| ≤ L|xk − x | ≤ Lρ < ρ
La successione è ben definita. Inoltre,
∗
∗
2
∗
k
∗
k
|xk − x | ≤ L|xk−1 − x | ≤ L |xk−2 − x | ≤ ... ≤ L |x0 − x | ≤ L ρ
Per k → ∞, limk→∞ Lk = 0 e dunque xk è convergente a x∗ .
Supposto per assurdo che y ∗ sia un punto fisso di g(x) in Iρ diverso da x∗ , si ha che:
∗
∗
∗
∗
∗
∗
∗
∗
|x − y | = |g(x ) − g(y )| ≤ L|x − y | < |x − y |
Ciò è assurdo.
Anche in questo caso si prova che:
Lk
∗
|xk − x | ≤
|x − x0 |
1−L 1
Propagazione degli errori nel metodo delle
approssimazioni successive
Poichè si opera in aritmetica finita anzichè su numeri reali, è impossibile
calcolare esattamente la funzione g(x) per x assegnato. Piuttosto, per
x assegnato, si calcola una approssimazione di g(x), data da
a(x) = g(x) + δ(x)
ove δ(x) è l’errore commesso. Di solito è nota una maggiorazione
di tale errore |δ(x)| ≤ δ . Pertanto operando in aritmetica finita, il
metodo delle approssimazioni successive diventa:
wk+1 = a(wk ) = g(wk ) + δk
k = 0, 1, 2, ...
ove wk è il k–esimo iterato ottenuto operando con numeri finiti e
|δk | ≤ δ . In generale la successione dei wk non converge. Tuttavia è
possibile determinare, sotto opportune condizioni, una approssimazione
di x∗ tanto più accurata quanto più δ è piccolo.
Teorema. Sia x∗ un punto fisso di g(x) e supponiamo che, in un
intervallo Iρ = [x∗ − ρ, x∗ + ρ], g(x) sia continua e sia contrattiva;
δ
allora, per ogni w0 ∈ Iρ0 = [x∗ −ρ0, x∗ +ρ0], con ρ0 = ρ− 1−L
, con
δ ≥ |δk |, la successione dei wk , ottenuta da wk = g(wk−1) + δk−1
è tale che:
∗
|wk − x | ≤
δ
δ
k
+ L (ρ0 −
)
1−L
1−L
e i wk appartengono a Iρ.
Nella diseguaglianza il primo termine è indipendente da k e può essere
grande se L è prossimo a 1; il secondo termine tende a 0 per k → ∞.
Pertanto non si ha più convergenza della successione degli iterati a x∗.
Si osservi che
|wk+1 − wk |
∗
∗
=
|wk+1 − x + x − wk | ≤
≤
|wk+1 − x | + |x − wk |
≤
+
=
∗
∗
δ
δ
k
+ L (ρ0 −
)+
1−L
1−L
δ
δ
k+1
+ L (ρ0 −
)=
1−L
1−L
2δ
δ
k
+ L (L + 1)(ρ0 −
)
1−L
1−L
Per quanto k sia preso grande, la differenza tra due iterati successivi non
2δ
può essere più piccola di 1−L
, a causa degli errori di arrotondamento
nel calcolo di g(x).
Criteri di arresto per il metodo delle
approssimazioni successive
Occorre determinare un criterio per vedere se l’approssimazione ottenuta
è punto fisso di g(x), ossia se x − g(x) = φ(x)f (x) = 0. Si ritiene
che xk sia una approssimazione accettabile se contemporaneamente:
|f (xk )| ≤ ²1
e |xk − xk−1| ≤ ²2
oppure
|f (xk )|
|xk − xk−1|
≤ σ1
e
≤ σ2
fmax
|xk |
ove ²1, ²2, σ1, σ2 sono tolleranze assegnate e fmax = maxx∈Iρ |f (x)|.
La scelta delle tolleranze è cruciale. Può essere che |f (xk )| sia piccola
pur non essendo xk accettabile e, viceversa, può essere che |f (xk )| sia
grande pur essendo xk accettabile.
2δ
, poichè questo termine
²2 deve essere inoltre maggiore o uguale a 1−L
che tiene conto degli errori di arrotondamento non converge a 0 per
k → ∞. xk − xk−1 può convergere a 0, pur essendo le due successioni
divergenti. Se non si conosce nulla di f (x), conviene applicare i test
relativi.
Ordine di convergenza
Definizione. Sia x∗ un punto fisso di g(x). Se per ogni x0 ∈ Iρ =
[x∗ − ρ, x∗ + ρ], la successione generata con l’iterazione funzionale è
tale che esistono una costante positiva C e un positivo p tale che
∗
∗ p
|xk − x | ≤ C|xk−1 − x |
k≥1
con C > 0 per p > 1 e 0 < C < 1 per p = 1, allora il metodo
di dice un metodo iterativo di ordine p. Se p = 1, il metodo si dice
lineare; se p = 2, si dice che ha velocità di convergenza quadratica,...
Teorema. Se x∗ un punto fisso di g(x) e se il metodo d’iterazione è
un metodo di ordine p, allora per ogni x0 ∈ Iρ = [x∗ − ρ, x∗ + ρ] la
successione degli {xk } → x∗ per k → ∞.
Dimostrazione. Dato x0 ∈ Iρ si ha che
∗
|xk − x |
≤
∗p
C1 |xk−1 − x |
∗
|xk − x |
≤
∗
C2 |xk−1 − x | p = 1, 0 < C2 < 1
p > 1, C1 > 0
Per p = 1, si ha:
∗
∗
k
∗
k
|xk − x | ≤ C2 |xk−1 − x | ≤ ... ≤ C2 |x0 − x | ≤ C2 ρ
k → 0. Inoltre x ∈ I .
Per k → ∞, limk→∞ xk = x∗ , perchè C2
ρ
k
Se p > 1,
∗
|xk − x |
≤
p
∗p
∗ p2
C1 |xk−1 − x | ≤ C1 C1 |xk−2 − x |
≤ ...
≤
1−pk
k−1
k
p
p
1−p
∗p
∗ pk
|x0 − x |
= C1
C1 C1 ...C1
|x0 − x |
=
=
1
p−1
∗ pk −1
∗
(C1
|x0 − x |)
|x0 − x |
1
p−1
Se vale che C1
ρ < 1, allora
1
1−p pk −1
∗
∗
|xk − x | ≤ (C1
ρ)
|x0 − x |
Allora xk ∈ Iρ e per k → ∞, limk→∞ xk = x∗ .
Poichè un metodo di ordine p è localmente convergente in un opportuno
intorno di x∗, la definizione di ordine di convergenza può essere data
anche in modo alternativo.
Un metodo iterativo che genera una successione di iterati {xk }
convergenti a x∗, si dice che è di ordine p o ha velocità di convergenza
pari a p se esistono costanti C e p tali che:
|xk+1 − x∗|
lim
=C
k→∞ |xk − x∗ |p
p>1
oppure
|xk+1 − x∗|
lim
= C p = 1, 0 < C < 1
k→∞ |xk − x∗ |
Se p = 1 e 0 < C < 1, il metodo si dice lineare. Se invece è
|xk+1 −x∗ |
limk→∞ |x −x∗|
k
= 0, il metodo è superlineare, mentre se il limite
vale 1, il metodo si dice sublineare.
C si dice costante asintotica di errore. Vale che
∗
∗ p
p
ek+1 = |xk+1 − x | ≈ C|xk − x | = Cek
o anche
p
ek+1 = (C + δk )ek
con limk→∞ δk = 0.
Teorema. Sia x∗ un punto fisso di g(x). Supponiamo che g(x) sia
di classe C p in un opportuno intervallo Iρ = [x∗ − ρ, x∗ + ρ] con
g (i)(x∗) = 0, i = 1, 2, ..., p − 1 e g p(x∗) 6= 0 e in modulo minore di
1 se p = 1. Allora per ogni x0 ∈ Iρ opportuno, il metodo di iterazione
funzionale è un metodo convergente di ordine p.
Dimostrazione. Poichè g(x) ∈ C p ed è g 0 (x) = 0 oppure |g 0 (x)| < 1 per p = 1, allora esiste un
intervallo Iρ = [x∗ − ρ, x∗ + ρ] per cui |g 0 (x)| ≤ L < 1 per x ∈ Iρ ed g(x) ∈ Iρ. Infatti,
x0 ∈ Iρ , e vale che
∗
|x1 − x |
=
∗
0
∗
|g(x0 − g(x )| = |g (ξ)||x0 − x |
<
∗
|x0 − x | < ρ
In generale
∗
|xk − x |
=
∗
∗
|g(xk−1 ) − g(x )| ≤ L|xk−1 − x | ≤ ...
≤
k
∗
L |x0 − x | < ρ
Dunque xk ∈ Iρ e xk → x∗ per k → ∞.
Se si considera lo sviluppo in serie di Taylor di punto iniziale x∗ , si ha:
xk+1
=
+
g p−1 (x∗ )
∗
0 ∗
∗
∗ p−1
g(xk ) = g(x ) + g (x )(x − x ) + ... +
(x − x )
+
(p − 1)!
g p (ξk )
p!
∗ p
(x − x )
con ξk ∈ (xk , x∗ ) ⊂ Iρ . Allora
p
p
p ∗
lim g (ξk ) = g ( lim (ξk )) = g (x )
k→∞
k→∞
e, poichè
segue
xk+1 − x∗
g p (ξk )
=
(xk − x∗ )p
p!
xk+1 − x∗
g p (x∗ )
lim
=
p!
k→∞ (xk − x∗ )p
Se p = 1, |g 0 (x∗ )| < 1.
Conseguenze.
1. Se x∗ è punto fisso di g(x) e g ∈ C 1, con g 0(x∗) 6= 0 ed è
|g 0(x∗)| < 1, allora esiste un intorno Iρ = [x∗ − ρ, x∗ + ρ] per
cui |g 0(x)| < 1 per x ∈ Iρ. In tale intervallo, per ogni x0 ∈ Iρ, il
metodo iterativo converge al punto fisso in modo lineare.
2. Se x∗ è punto fisso di g(x) e g ∈ C 2, con g 0(x∗) = 0 e
g 00(x∗) 6= 0, allora esiste un intorno Iρ = [x∗ − ρ, x∗ + ρ] tale
che, per ogni x0 ∈ Iρ, il metodo iterativo converge al punto fisso
con velocità di convergenza quadratica e vale che
g 00(x∗)
xk+1 − x∗
lim
=
k→∞ (xk − x∗ )2
2
o equivalentemente
g 00(ξk )
∗ 2
xk+1 − x =
(xk − x )
2
∗
con ξk ∈ Iρ.
Se M è un valore maggiorante della derivata seconda di g(x) in
Iρ, allora
M 2
|ek+1| ≤
ek
2
M
2 è la costante che maggiora l’errore il cui valore asintotico è
g 00 (x∗ )
.
2
Data l’equazione f (x) = 0, si può determinare x∗, soluzione di
f (x) = 0, come punto fisso di
x = x − φ(x)f (x) = g(x)
con φ(x) 6= 0 per ogni x nell’intervallo in cui si cerca la soluzione.
Per esaminare la velocità di convergenza, si consideri g 0(x):
0
0
0
g (x) = 1 − φ(x)f (x) − φ (x)f (x)
In x∗, g 0(x∗) = 1 − φ(x∗)f 0(x∗). Il metodo iterativo ha velocità di
0
∗
1
convergenza lineare se φ0(x∗) 6= f 0(x
∗ ) , supposto che f (x ) 6= 0. Se
1
φ(x) è costante, φ(x) = m 6= f 0(x
∗ ) , il metodo è lineare.
La convergenza è quadratica se
∗
φ(x ) =
1
f 0(x∗)
con f 0(x∗) 6= 0. Allora o si pone φ(x) =
incognito), oppure si pone
φ(x) =
1
f 0 (x∗ )
costante (ma x∗ è
1
f 0(x)
ottenendo un metodo a convergenza quadratica dato da
xk+1 = xk −
f (xk )
f 0(xk )
Il metodo è detto metodo di Newton. Vale che
f 0(x∗)2 − f (x∗)f 00(x∗)
f (x∗)f 00(x∗)
g (x ) = 1 −
=
=0
f 0(x∗)2
f 0(x∗)2
0
∗
f 00(x∗)
g (x ) = 0 ∗
f (x )
Allora se f (x∗) = 0, f 0(x∗) 6= 0, f 00(x∗) 6= 0, il metodo di Newton
ha convergenza quadratica con costante asintotica di convergenza
f 00 (x∗ )
.
2f 0 (x∗ )
00
∗
Si dice anche metodo delle tangenti, perchè geometricamente xk+1
è il punto d’intersezione tra y = 0 e la retta tangente a f (x) in
(xk , f (xk )):
0
y = f (xk ) + f (xk )(x − xk )
8
7
f(x)
6
5
4
3
2
1
x*
0
x2
−1
0
0.5
1
x1
1.5
x0
2
2.5
3
Riassumiamo tutte le condizioni per la convergenza locale del metodo
di Newton:
Sia x∗ uno zero di f (x). Sia f (x) continua insieme alle sue derivate
prima, seconda e terza (continuità di g, g 0, g 00). Sia f 0(x) 6= 0 per x in
un opportuno interno di x∗ e sia f 00(x∗) 6= 0 ( ff0(x)
deve essere definita
(x)
e deve essere g 00(x∗) 6= 0). Allora, per ogni x∗ ∈ [x∗ − ρ, x∗ + ρ],
la successione generata dal metodo di Newton converge a x∗ in modo
quadratico.
Esempi.
¡ x ¢2
1. sin(x) − 2 = 0 in [1, 2].
f 00(x) = − sin(x) − 12
f 0(x) = cos(x) − x2 ;
¡ x ¢2
sin(xk ) − 2k
xk+1 = xk −
x
cos(xk ) − 2k
k
0
1
2
3
4
xk
1.5
2.14039
1.95201
1.93393
1.93375
f 0(xk )
-0.67926
-1.60948
-1.34805
-1.32217
f (xk )
0.434995
-0.303197
-0.024372
-0.000233
0.000005
Costante asintotica di errore
g 00 (x∗ )
2
2. x2 − γ = 0
xk+1
1
=
2
µ
=
−f (xk )/f 0(xk )
0.64039
-0.18838
-0.01808
-0.00018
f 00 (x∗ )
2f 0 (x∗ )
γ
xk +
xk
' 0.54.
¶
Per γ = 2, e [1, 2], si ha:
k
xk
0
1.5
1
1.41666666
2
1.41421568
3 1.414213561
4 1.414213562
La costante asintotica di errore vale f 00(x∗)/(2f 0(x∗)) =
√
1/(2 γ). Se γ è piccolo, la convergenza può essere lenta.
La complessità del metodo è pari a una valutazione di funzione e una
valutazione della derivata prima per passo; se la complessità di f 0 è
analoga a quella di f , si dice che il metodo richiede due valutazioni di
funzioni per passo.
Condizioni per la convergenza globale del
metodo di Newton
Teorema. Sia f ∈ C 2[a, b]. Sia inoltre:
1.
2.
3.
4.
f (a) < 0, f (b) > 0;
f 0(x) 6= 0;
f 00(x) ≤ 0;
|f (b)| ≤ (b − a)|f 0(b)|.
Allora il metodo di Newton genera una successione di iterati convergenti
all’unica soluzione di f (x) = 0 appartenente ad [a, b] a partire da un
qualunque x0 ∈ [a, b].
Il teorema resta valido se valogono le seguenti condizioni:
1. f (a) < 0, f (b) > 0;
2. f 0 (x) 6= 0;
3. f 00 (x) ≥ 0;
4. |f (a)| ≤ (b − a)|f 0 (a)|.
oppure
1. f (a) > 0, f (b) < 0;
2. f 0 (x) 6= 0;
3. f 00 (x) ≥ 0;
4. |f (b)| ≤ (b − a)|f 0 (b)|.
e, rispettivamente,
1. f (a) > 0, f (b) < 0;
2. f 0 (x) 6= 0;
3. f 00 (x) ≤ 0;
4. |f (a)| ≤ (b − a)|f 0 (a)|.
Definizione. Si dice che x∗ è uno zero di f (x) di molteplicità m se
f (x) = (x − x∗)mq(x), x 6= x∗, e limx→x∗ q(x) 6= 0.
Se m = 1, x∗ è uno zero semplice.
Teorema. Sia f ∈ C 0[a, b], ove [a, b] contiene uno zero x∗ di f (x).
x∗ è uno zero semplice ⇔ f (x∗) = 0, f 0(x∗) 6= 0.
Dimostrazione. Se x∗ è uno zero semplice, f (x∗ ) = 0 e f (x) = (x − x∗ )q(x), con
limx→x∗ q(x) 6= 0. Vale che:
0
∗ 0
f (x) = (x − x )q (x) + q(x)
Allora
0
0 ∗
lim f (x) = f (x ) = lim q(x) 6= 0
x→x∗
x→x∗
Se, viceversa, f (x∗ ) = 0, f 0 (x∗ ) 6= 0, allora
∗
∗ 0
∗ 0
f (x) = f (x ) + (x − x )f (ξ) = (x − x )f (ξ)
con ξ compreso tra x e x∗ . Posto q(x) = f 0 (ξ), si ha limx→x∗ f 0 (ξ) = f 0 (limx→x∗ ξ) =
f 0 (x∗ ) 6= 0.
Teorema. Sia f ∈ C m[a, b], ove [a, b] contiene uno zero x∗ di f (x).
x∗ è uno zero di molteplicità m ⇔ f (i)(x∗) = 0, i = 0, 1, ..., m−1
ed è f m(x∗) 6= 0.
Se x∗ è uno zero semplice di f (x), il metodo di Newton converge
quadraticamente.
Se x∗ è uno zero di molteplicità m, allora poichè
f (x) = (x − x∗)mq(x), con limx→x∗ q(x) 6= 0,
0
f (x)
=
∗ m−1
∗ m 0
m(x − x )
q(x) + (x − x ) q (x) =
=
∗ m−1
∗ 0
(x − x )
(mq(x) + (x − x )q (x))
=
∗ m−2
∗ m−1 0
m(m − 1)(x − x )
q(x) + m(x − x )
q (x) +
+
∗ m−1 0
∗ m 00
m(x − x )
q (x) + (x − x ) q (x) =
=
∗ m−2
(x − x )
.
.
0
∗
∗ 2 00
(m(m − 1)q(x) + 2mq (x)(x − x ) + (x − x ) q (x))
f (x)
f 0 (x)
=
∗
(x − x )
0
g (x)
=
f (x)f 00 (x)
f 0 (x)2
=
q(x)(m(m − 1)q(x) + 2mg 0 (x)(x − x∗ ) + (x − x∗ )2 q 00 (x))
=
(mq(x) + (x − x∗ )q 0 (x))2
=
(m2 − m)q(x∗ )2
1
=1−
6 0
=
m
m2 q(x∗ )2
00
f (x)
0 ∗
g (x )
q(x)
mq(x) + (x − x∗ )q 0 (x)
com m > 1. E’ g 0(x∗) < 1. Dunque il metodo di Newton diventa
convergente solo linearmente. Tuttavia se si modifica l’iterazione nel
seguente modo:
f (xk )
xk+1 = xk − m 0
f (xk )
la convergenza ritorna almeno quadratica:
f (x∗)f 00(x∗)
1
g (x ) = 1 − m + m
= 1 − m + m(1 − ) = 0
f 0(x∗)2
m
0
∗
Un altro modo per ottenere un metodo a convergenza quadratica
q(x)
∗
consiste nell’osservare che ff0(x)
=
(x
−
x
)
ha in
(x)
(mq(x)+(x−x∗ )q 0 (x))
x∗ uno zero di molteplicità 1. Dunque si applica il metodo di Newton
a ff0(x)
:
(x)
xk+1
f (xk )/f 0(xk )
= xk − 0
(f (xk )2 − f (xk )f 00(xk ))/f 0(xk )2
Se g(x) è sufficientemente regolare in un opportuno intervallo che
contiene x∗, allora si ha convergenza quadratica al punto fisso x∗.
Per xk sufficientemente vicino a x∗, f 0(x∗) e f (x∗) sono piccoli e si
possono avere problemi di cancellazione.
Il metodo di Newton si può derivare considerando lo sviluppo in serie
di Taylor a partire da xk e calcolandolo in x∗, trascurando i termini di
ordine superiore a 1.
∗
0 = f (x )
⇒
=
f 00(ξ) ∗
2
f (xk ) + f (xk )(x − xk ) +
(x − xk )
2
f (xk )
∗
x ' xk − 0
f (xk )
0
∗
Se si sostituisce la funzione f (x) con il polinomio di grado 1 tale che
p(xk ) = f (xk ) e p0(xk ) = f 0(xk ) (modello lineare di f (x)), si
ottiene il metodo di Newton.
Se si sostituisce la funzione f (x) con il polinomio di grado 2 anzichè
di grado 1, tale che il polinomio coincide con f (x) fino alla derivata
seconda, si ottiene la seguente iterazione funzionale:
0
xk+1 = xk −
f (xk ) ±
p
f 0(xk )2 − 2f (xk )f 00(xk )
f 00(xk )
Per uno zero semplice, il metodo ha ordine di convergenza 3.
Tuttavia queste iterazioni funzionali comportano alta complessità poichè
richiedono il calcolo non solo della funzione ma anche delle derivate ad
ogni passo.
Anzichè usare polinomi di Taylor per approssimare f (x) e calcolarne
uno zero, si possono usare polinomi di interpolazione. Da tale idea
nascono i metodi di interpolazione per la determinazione degli zeri di
una funzione.
Regula falsi
Sia a1 ≡ a, b1 ≡ b, tali che f (a).f (b) < 0, con f ∈ C[a, b]. Per
ogni k = 1, 2, ... si costruisce a partire da [ak , bk ] con f (ak )·f (bk ) <
0 una successione di iterati dati da:
ck+1 = bk −
f (bk
f (bk )−f (ak )
bk −ak
. Geometricamente ck+1 è l’intersezione tra l’asse delle x e la retta che
unisce i punti di coordinate (ak , f (ak )) e (bk , f (bk )):
y
=
0
y
=
f (bk ) +
f (bk ) − f (ak )
(x − bk )
bk − ak
Si calcola ck+1 e si pone
½
[ak+1, bk+1] =
[ak , ck+1]
[ck+1, bk ]
f (ak )f (ck+1) < 0
f (ak )f (ck+1) > 0
Se f (ck+1) = 0, x∗ = ck+1.
La regula falsi è convergente. L’ordine di convergenza è lineare.
Non è detto che abbia maggiore efficienza del metodo di bisezione. Ciò
dipende dalla particolare scelta della funzione. Si veda il comportamento
di f (x) = sin(x) − 0.9 nell’intervallo [0, 1.5].
Metodo delle secanti
xk+1 = xk −
f (xk )
f (xk )−f (xk−1 )
xk −xk−1
xk+1 è intersezione tra y = 0 e il polinomio che interpola f (x)
nei punti (xk−1, f (xk−1)) e (xk , f (xk )). Tuttavia non è detto che
f (xk ) e f (xk−1) siano di segno contrario (questo può dare problemi
di cancellazione che non ci sono con la regula falsi).
Si ha bisogno di due approssimazioni iniziali. La convergenza è ottenibile
solo se x0 e x1 appartengono a un intervallo sufficientemente piccolo
attorno a x∗, zero di f (x).
Se f ∈ C 2, si può dimostrare che il metodo delle secanti genera una
successione di iterati che converge alla soluzione x∗ con velocità di
convergenza frazionaria data da p = 1.618..., ove p à soluzione di
p2 − p − 1 = 0. Posto ek = M |xk − x∗|, ove M è una costante
positiva, si ha che:
ek+1 ≤ (K)
pk+1
pk p
= (K )
ove K è una costante positiva minore di 1.
Un passo del metodo delle secanti richiede una sola valutazione di
funzione. Dunque due passi hanno la stessa complessità del metodo
di Newton. Per quanto riguarda la convergenza, si ha: ek+2 ≤
k+2
k
2
k
= (K p )p ≤ (K p )p+1perchè p2 = p + 1. Per cui
(K)p
si un procedimento con velocità di convergenza p + 1 = 2.618...,
localmente più veloce di quello di Newton.
Generalizzazione del metodo delle secanti
Dati r + 1 valori approssimati xk , xk−1, ..., xk−r , si determina xk+1
come intersezione tra y = 0 e il polinomio di grado r , tale che
f (xk−i) = p(xx−i),
i = 0, 1, ..., r
Per r = 1, si ottiene il metodo delle secanti.
Per r = 2, si ottiene il metodo di Muller. Dati xk , xk−1, xk−2, si
determina
2
p(x) = a(x − xk ) + b(x − xk ) + c
tali che
p(xk )
=
f (xk ) = c
p(xk−1 )
=
2
f (xk−1 ) = a(xk−1 − xk ) + b(xk−1 − xk ) + c
p(xk−2 )
=
2
f (xk−2 ) = a(xk−2 − xk ) + b(xk−2 − xk ) + c
⇒
c
=
f (xk )
b
=
(xk−2 − xk )2 (f (xk−1 ) − f (xk )) − (xk−1 − xk )2 (f (xk−2 ) − f (xk ))
(xk−2 − xk )(xk−2 − xk−1 )(xk−1 − xk )
a
=
(xk−1 − xk )(f (xk−2 ) − f (xk )) − (xk−2 − xk )(f (xk−1 ) − f (xk ))
(xk−2 − xk )(xk−2 − xk−1 )(xk−1 − xk )
xk+1 = xk −
√
2c
b ± b2 − 4ac
Il segno è scelto in modo che xk+1 − xk sia più piccolo possibile, ossia
la quantità al denominatore più grande possibile:
xk+1 = xk −
2c
√
b + segno(b) b2 − 4ac
Se f ∈ C 3 e f 0(x∗) =
6 0, in prossimità di x∗ si ha convergenza con
ordine di convergenza p = 1.84, ove p è radice di p3 = p2 + p + 1.
Il metodo delle secanti possiede un’altra generalizzazione. Se f (x)
nell’intorno di x∗ è biunivoca, allora essa è invertibile, ossia esiste una
funzione g(y) tale che g(f (x)) = x. Pertanto vale che g(f (x∗)) =
g(0) = x∗.
Allora a partire da f (xk ), ..., f (xk−r ) si può costruire un polinomio
q(y) di grado r tale che q(f (xk−i)) = xk−i, i = 0, ..., r . Si
considera come nuovo iterato xk+1 il valore di q(0). Questi metodi
vengono detti metodi dell’interpolazione inversa. Per r = 1 si riottiene
il metodo delle secanti, per r = 2 il metodo dell’interpolazione
quadratica inversa. Si tratta di costruire un polinomio q(y) di grado 2
2
q(y) = α1y + α2y + α3
che passa per i punti (f (xk ), xk ), (f (xk−1), xk−1), (f (xk−2), xk−2),
e di considerare come nuovo iterato xk+1 = q(0) = α3. Il
procedimento viene poi reiterato.
La funzione di Matlab fzero è un polialgoritmo che usa al suo
interno il metodo di bisezione, il metodo delle secanti e il metodo
dell’interpolazione quadratica inversa. Si sceglie un metodo piuttosto
che l’altro in modo da garantire convergenza globale.