LIMITI DELLE FUNZIONI DI UNA VARIABILE
Con lo studio del limite si vuole verificare il comportamento della funzione in prossimità di un punto
x0 a prescindere se la funzione è definita in esso oppure il comportamento della funzione quando alla
variabile x si danno dei valori sempre più grandi o sempre più piccoli.
1° esempio : data la funzione y = 2 x + 3 studiamo il comportamento della funzione nell’intorno
completo del punto x = 3
valore della x
intorno sinistro di 3
2,90
2,92
2,94
2,96
2,98
2,99
2,999
valore della
funzione
f (x )
valore della x
intorno destro di 3
8,800
8,840
8,880
8,920
8,960
8,980
8,9980
3,20
3,10
3,05
3,04
3,03
3,02
3,01
valore della
funzione
f (x )
9,400
9,200
9,100
9,080
9,060
9,040
9,020
Dall’esame della tabella si evince che se alla variabile x diamo valori prossimi al 3 , avvicinandoci
sia da destra che da sinistra, la funzione f (x ) tende ad avvicinarsi sempre più ad un valore
determinato , nel caso f (x ) tende a 9 .
2
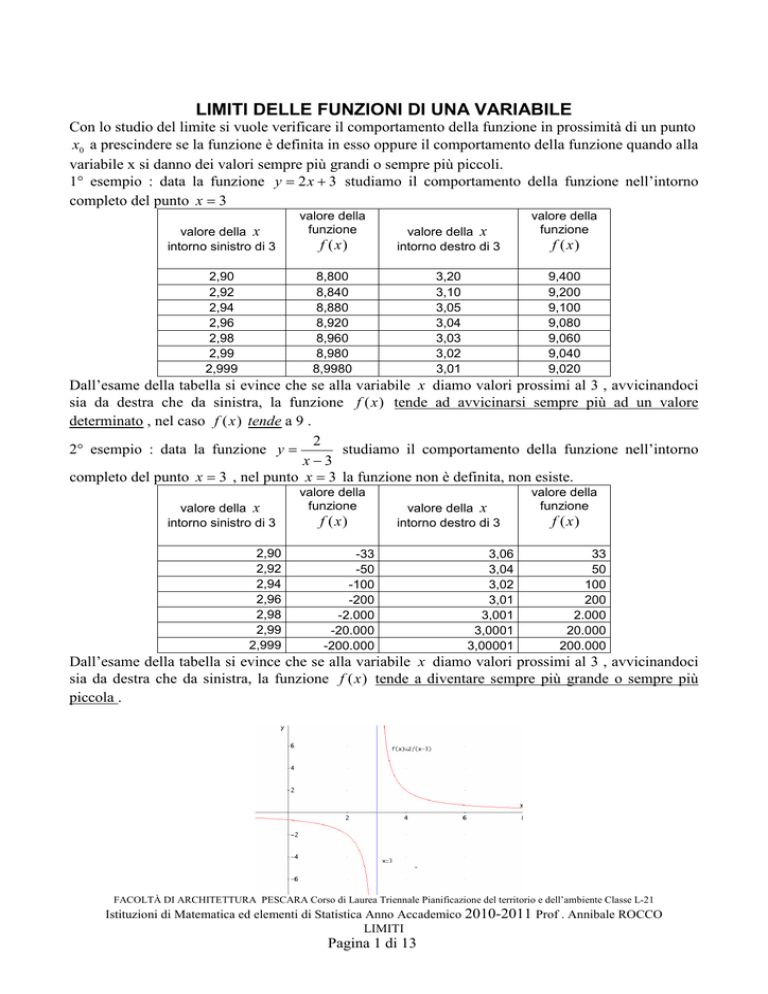
2° esempio : data la funzione y =
studiamo il comportamento della funzione nell’intorno
x−3
completo del punto x = 3 , nel punto x = 3 la funzione non è definita, non esiste.
valore della x
intorno sinistro di 3
2,90
2,92
2,94
2,96
2,98
2,99
2,999
valore della
funzione
f (x )
valore della x
intorno destro di 3
-33
-50
-100
-200
-2.000
-20.000
-200.000
3,06
3,04
3,02
3,01
3,001
3,0001
3,00001
valore della
funzione
f (x )
33
50
100
200
2.000
20.000
200.000
Dall’esame della tabella si evince che se alla variabile x diamo valori prossimi al 3 , avvicinandoci
sia da destra che da sinistra, la funzione f (x ) tende a diventare sempre più grande o sempre più
piccola .
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 1 di 13
1° caso LIMITE FINITO PER
lim
x → x0
f ( x) = l
x
TENDENTE AD UN VALORE FINITO :
limite di x che tende a x0 di f(x) è uguale a l
Scelto un numero positivo ε piccolo a piacere è possibile determinare in corrispondenza di ε un
intorno completo di x0 dipendente da ε , ε U x 0 , tale che per ogni valore x di tale intorno ( escluso al
più il valore x0 ) sia verificata la relazione
f ( x) − l < ε oppure l’equivalente l − ε < f ( x) < l + ε .
In generale scelto a piacere il valore di ε > 0 se la disequazione f ( x) − l < ε oppure l’equivalente
l − ε < f ( x) < l + ε costituisce un intorno completo di x0 allora il limite della funzione nel punto è
proprio l .
Esempio: data la funzione f ( x ) = 3 x + 2 verificare che lim 3x + 2 = 5
x →1
Bisogna verificare se la disequazione
3x + 2 − 5 < ε costituisce un intorno completo di x0 ;
3 x − 3 ≥ 0
3 x − 3 < 0
3x + 2 − 5 < ε ; 3x − 3 < ε ;
oppure
; le soluzioni del doppio sistema
3 x − 3 < ε
3 x − 3 > −ε
sono 1 −
ε
3
f(x)=3x+2
< x < 1+
ε
3
, l’intervallo costituisce effettivamente un intorno completo del punto 1 .
Scelto il valore di ε i valori l + ε , l − ε riportati sull’asse delle
ascisse danno luogo ad un intorno completo del punto 1;
qualunque valore preso all’interno dell’intorno verifica la
relazione f ( x) − l < ε come si verifica facilmente dal grafico.
RISOLUZIONE NUMERICA
Scelto una valore di ε , esempio ε = 0,5 , l + ε = 5 + 0,5 = 5,5 e
l − ε = 5 − 0,5 = 4,5 , bisogna verificare che i relativi valori
delle ascisse costituiscono un intorno completo del punto 1.
−
5,5 − 2
= 1,16 e
3
−
4,5 − 2
l − ε = 4,5;3 x + 2 = 4,5; x =
= 0,8 3 , l’intervallo costituisce
3
l + ε = 5,5;3x + 2 = 5,5; x =
effettivamente un intorno completo del punto 1 .
Preso un valore x0 all’interno dell’intorno , esempio x0 = 1,05 il corrispondente valore della
funzione sarà y = f (1,05) = 5,15 e pertanto risulterà verificata la relazione
f ( x) − l < ε ,
5,15 − 5 < 0,5 ,il limite della funzione per x → 1 è proprio il valore f ( x ) = 5 .
Scelto una valore ancora più piccolo di ε , esempio ε = 0,1 , l + ε = 5 + 0,1 = 5,1 e
l − ε = 5 − 0,1 = 4,9 , bisogna verificare che i relativi valori delle ascisse costituiscono un intorno
completo del punto 1.
−
−
5,1 − 2
4,9 − 2
l + ε = 5,1;3 x + 2 = 5,1; x =
= 1,0 3 e l − ε = 4,9;3x + 2 = 4,9; x =
= 0,9 6 , l’intervallo
3
3
tende a restringersi ma è sempre un intorno completo del punto 1 . Qualunque valore preso
all’interno dell’intorno verificherà la relazione f ( x) − l < ε .
•
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 2 di 13
I valori di e e dell’intorno di x0 sono direttamente connessi , scelto l’uno si otterrà il valore
dell’altro ; nell’esercizio precedente scelto l’estremo superiore o l’estremo inferiore dell’intorno a
piacere avremo il corrispondente valore di e in modo tale che sia sempre verificata la relazione
f ( x) − l < ε .
LIMITE DESTRO PER
x
TENDENTE AD UN VALORE FINITO : lim+
x → x0
f ( x) = l
Scelto un numero positivo ε piccolo a piacere è possibile determinare in corrispondenza di ε un
intorno DESTRO di x0 , ε U x 0 , tale che per ogni valore x di tale intorno sia verificata la relazione
f ( x ) − l < ε oppure l’equivalente f ( x ) < l + ε .
LIMITE SINISTRO PER
x
TENDENTE AD UN VALORE FINITO : lim−
x → x0
f ( x) = l
Scelto un numero positivo ε piccolo a piacere è possibile determinare in corrispondenza di ε un
intorno SINISTRO di x0 , ε U x0 , tale che per ogni valore x di tale intorno sia verificata la relazione
f ( x ) − l > −ε oppure l’equivalente f ( x ) > l − ε .
2° caso LIMITE FINITO PER
x
TENDENTE AD UN VALORE INFINITO :
lim
f ( x) = l
x→∞
Scelto un numero positivo ε piccolo a piacere è possibile determinare un numero reale positivo k
tale che per ogni x > k ( intorno dell’infinito ) ε U ∞ risulti la relazione
f ( x) − l < ε oppure
l’equivalente l − ε < f ( x) < l + ε .
La retta y = l viene chiamata ASINTOTO ORIZZONTALE .
In generale scelto a piacere il valore di ε > 0 se la disequazione f ( x) − l < ε oppure l’equivalente
l − ε < f ( x) < l + ε costituisce un intorno dell’infinito ε U ∞ allora il limite della funzione nel punto
è proprio l .
Esempio: data la funzione f ( x ) =
2x + 1
2x + 1
=2
verificare che lim
x→∞
x
x
2x + 1
− 2 < ε costituisce un intorno dell’infinito;
x
1
> 0; x > 0
< 0; x < 0
x
oppure
; le soluzioni del doppio sistema
1
1
1
< ε; x >
x > −ε ; x < − e
e
Bisogna verificare se la disequazione
1
2x + 1
1
x
−2 <ε ;
<ε ;
x
x
1
x
1
1
sono x < − ∨ x > , l’intervallo costituisce effettivamente un intorno dell’infinito.
e
e
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 3 di 13
Scelto il valore di ε si ottiene il valore l + ε che riportato sull’asse delle ascisse ci darà il valore di
x = k ; per tutti i valori x > k sarà sempre verificata la relazione f ( x) − l < ε come si verifica
facilmente dal grafico.
RISOLUZIONE NUMERICA
2x + 1
Scelto una valore di ε , esempio ε = 0,5 , l + ε = 2 + 0,5 = 2,5 ,
= 2,5 , x = k = 2 , per tutti i
x
7
7
1
valori di k > 2 deve valere la disequazione f ( x) − l < ε , preso k = 3 f (3) = e quindi − 2 =
3
3
3
valore che effettivamente è minore di ε = 0,5 .
I valori di e e k sono direttamente connessi , scelto l’uno si otterrà il valore dell’altro ;
nell’esercizio precedente scelto un valore di k grande a piacere avremo il corrispondente valore di e
in modo tale che sia sempre verificata la relazione f ( x) − l < ε .
LIMITE FINITO PER
x
TENDENTE A PIÙ INFINITO : lim
f ( x) = l
x→+∞
Scelto un numero positivo ε piccolo a piacere è possibile determinare un numero reale positivo k
tale che per ogni x > k ( intorno di più infinito ) risulti la relazione
f ( x) − l < ε oppure
l’equivalente l − ε < f ( x) < l + ε .
LIMITE FINITO PER
x
TENDENTE A MENO INFINITO : lim
f ( x) = l
x→−∞
Scelto un numero positivo ε piccolo a piacere è possibile determinare un numero reale positivo k
tale che per ogni x < − k ( intorno di meno infinito ) risulti la relazione
f ( x) − l < ε oppure
l’equivalente l − ε < f ( x) < l + ε .
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 4 di 13
3° caso LIMITE INFINITO PER
lim
x → x0
x
TENDENTE AD UN VALORE FINITO :
f ( x) = ∞
Scelto un numero positivo E grande a piacere è possibile determinare un intorno completo di x0 ,
E U x 0 , tale che per ogni valore x di tale intorno ( escluso al più il valore x0 ) risulti la relazione
f ( x) > E oppure l’equivalente f ( x) < − E oppure f ( x) > E .
In questo caso la retta x = x0 è un ASINTOTO VERTICALE.
In generale scelto a piacere il valore di E > 0 se la disequazione f ( x ) > E oppure l’equivalente
f ( x ) > E ∨ f ( x ) < − E costituisce un intorno di x0 allora il limite della funzione nel punto vale
infinito .
Esempio: data la funzione f ( x ) =
2
2
=∞
verificare che lim
x →3 x − 3
x−3
2
> E costituisce un intorno di 3
x−3
2
2
x
−
3
≥
0
x
≥
3
≥
0
< 0 x − 3 < 0
x < 3
2
x − 3
x − 3
; x −3 1 ;
;x −3
>E ;
2 ;
1 ;
2
x−3
2 > E 2 < E x < 3 + E 2 < − E 2 > − E x > 3 − E
x − 3
x − 3
2
2
le soluzioni del doppio sistema sono 3 − < x < 3 + e rappresenta un intorno completo di 3.
E
E
Preso un numero positivo E grande a piacere sull’asse
delle y il rispettivo valore dell’ascissa cade a destra di 3,
ottenendo un intorno destro di 3 3 + δ con δ un
parametro positivo dipendente da E. In corrispondenza
dell’opposto di E si trova l’intorno sinistro di 3 3 − δ .
E’ stato costituito, pertanto, un intorno completo del
punto 3. Qualunque valore x all’interno dell’intorno
avrà l’ordinata della funzione sempre maggiore di E
qualunque valore si attribuirà a E, ovvero vale la
disequazione:
f ( x ) > E o l’equivalente f ( x ) > E
∨ f ( x) < − E
2
2
, posto E = 100 la funzione diventa 100 =
RISOLUZIONE NUMERICA: f ( x ) =
x−3
x−3
x−3
1
2
=
; x = 3+
; x = 3,02 , intorno destro del punto 3;
2
100
100
2
posto E = -100 la funzione diventa − 100 =
x−3
x−3
1
2
=−
; x = 3−
; x = 2,98 , intorno sinistro del punto 3 e pertanto si è ottenuto un intorno
2
100
100
completo del punto 3 .
Preso un valore all’interno dell’intorno destro , esempio x = 3,01 , la funzione in tale punto dovrà
essere più grande di E , f (3,01) = 200 .
Occorre verificare se la disequazione
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 5 di 13
Preso un valore all’interno dell’intorno sinistro, esempio x = 2,99 , la funzione in tale punto dovrà
essere più piccola di –E, f ( 2,99) = −200 , verificate le due condizioni il limite è proprio infinito .
Le condizioni si verificano per tutti i punti all’interno dell’intorno completo del punto 3 .
Nei seguenti grafici sono riportate le possibili situazioni di comportamento delle funzioni :
−2
il
x−3
comportamento della funzione quando
la x si avvicina a 3 è descritto dal
grafico e può essere sintetizzato dai due
limiti:
f ( x) =
Data la funzione
−2
lim x − 3 = −∞
x → 3+
intorno destro E > 0, f ( x ) < − E
−2
lim x − 3 = +∞
x → 3−
intorno sinistro E > 0, f ( x ) > E
−2
il
(x − 3)2
comportamento della funzione quando
la x si avvicina a 3 è descritto dal
grafico e può essere sintetizzato da
limite:
−2
lim
= −∞
x → 3 ( x − 3)2
intorno completo del punto 3
E > 0, f ( x ) < − E
Data la funzione
f ( x) =
2
il
(x − 3)2
comportamento della funzione quando la
x si avvicina a 3 è descritto dal grafico e
può essere sintetizzato da limite:
2
lim
= +∞
x → 3 ( x − 3)2
intorno
completo
del
punto
3
E > 0, f ( x ) > E
Data la funzione
f ( x) =
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 6 di 13
LIMITE INFINITO PER
x
TENDENTE AD UN VALORE INFINITO : lim
f ( x) = ∞
x→∞
Scelto un numero positivo E grande a piacere è possibile determinare un intorno di infinito E U ∞ tale
che per ogni valore x di tale intorno risulti la relazione
f ( x) > E oppure l’equivalente
f ( x) < − E oppure f ( x) > E .
In generale scelto a piacere il valore di E > 0 se la disequazione f ( x ) > E oppure l’equivalente
f ( x ) > E ∨ f ( x ) < − E costituisce un intorno dell’infinito E U ∞ allora il limite della funzione nel
punto vale infinito .
x2 + 1
quando la
x
x diventa sempre più grande o sempre
più piccola la f(x) diventa sempre più
grande o sempre più piccola.
Il grafico può essere rappresentato dai
seguenti limiti:
x2 + 1
x2 + 1
lim
= +∞ e lim
= −∞
x → +∞
x → −∞
x
x
Data la funzione f ( x ) =
− x2 + 1
quando
x
la x diventa sempre più grande o sempre
più piccola la f(x) diventa sempre più
piccola o sempre più grande.
Il grafico può essere rappresentato dai
seguenti limiti:
− x2 + 1
− x2 + 1
lim
= −∞ e lim
= +∞
x → +∞
x → −∞
x
x
Data la funzione f ( x ) =
− x2 + 1
− x2 + 1
Esempio: lim
= +∞ , preso E=100 f ( x ) =
= 100; x ≈ +0,01 ∨ x ≈ −100,01
x → −∞
x
x
x < −100,01 risulterà verificata la relazione f ( x ) > E; f ( x ) > 100 ;
preso x = −101 risulta f ( −101) = 100,99 e quindi f ( x ) > 100
per ogni
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 7 di 13
TEOREMI SUI LIMITI
1°. teorema sull’unicità del limite: se lim f ( x ) = l l , il limite, è unico;
x → x0
2°. teorema della permanenza del segno: se lim f ( x ) = l e l ≠ 0 ,esiste un intorno del punto x0
x → x0
all’interno del quale la funzione f (x ) assume lo stesso segno del suo limite;
3°. teorema del confronto: date tre funzioni definite tutte nello stesso intervallo escluso al più un
punto x0 ,se risulta f ( x ) ≤ g ( x ) ≤ γ ( x ) e lim f ( x ) = l , lim γ ( x ) = l allora sarà anche lim g ( x ) = l
x → x0
x → x0
x → x0
OPERAZIONI CON I LIMITI
CONDIZIONE INIZIALE: le funzioni f (x ) e g (x ) siano definite nello stesso intervallo escluso al
più un punto x0 ed esistano e siano finiti i limiti lim f ( x ) = l1 e lim g ( x ) = l2 .
x → x0
x → x0
TEOREMI:
1°. SOMMA DI DUE FUNZIONI : lim [ f ( x ) + g ( x )] = lim f ( x ) + lim g ( x ) = l1 + l2 il limite della
x → x0
x→ x0
x → x0
somma di due funzioni è uguale alla somma dei limiti delle due funzioni.
OSSERVAZIONE:
se uno o entrambi i limiti non sono finiti valgono le seguenti relazioni:
l1 = +∞, l2 = finito → l1 + l2 = +∞
l1 = −∞, l2 = finito → l1 + l2 = −∞
l1 = l2 = −∞, → l1 + l2 = −∞
l1 = l2 = +∞, → l1 + l2 = +∞
l1 = +∞, l2 = −∞ → l1 + l2 = +∞ − ∞ FORMA INDETERMINATA, non è possibile stabilire
immediatamente il risultato dell’operazione ma è necessario procedere con altri sviluppi.
Per quanto riguarda la differenza di due funzioni le operazioni restano le stesse con l’attenzione che
la forma indeterminata è la differenza di due funzioni che tendono all’infinito con lo stesso segno.
2°. PRODOTTO DI DUE FUNZIONI : lim [ f ( x ) ⋅ g ( x )] = lim f ( x ) ⋅ lim g ( x ) = l1 ⋅ l2 il limite del
x → x0
x → x0
x → x0
prodotto è uguale al prodotto dei limiti ;
OSSERVAZIONE:
se uno o entrambi i limiti non sono finiti valgono le seguenti relazioni:
• per i risultati valgono le regole del prodotto
l1 = +∞, l2 = finito → l1 ⋅ l2 = +∞
l1 = −∞, l2 = finito → l1 ⋅ l2 = −∞
l1 = l2 = +∞, → l1 ⋅ l2 = +∞
l1 = l2 = −∞, → l1 ⋅ l2 = +∞
l1 = −∞, l2 = +∞ → l1 ⋅ l2 = −∞
• se uno dei due limiti tende a zero e l’altro a infinito , l1 = +∞, l2 = 0 → l1 ⋅ l2 = 0 ⋅ ∞ FORMA
INDETERMINATA, non è possibile stabilire immediatamente il risultato dell’operazione ma è
necessario procedere con altri sviluppi.
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 8 di 13
•
QUOZIENTE DI DUE FUNZIONI : se, oltre alla condizione iniziale, si aggiunge l’ipotesi che
l2 ≠ 0 lim [ f ( x ) ÷ g ( x )] = lim f ( x ) ÷ lim g ( x ) = l1 ÷ l2 il limite del quoziente è uguale al
x → x0
x→ x0
x → x0
quoziente dei limiti.
OSSERVAZIONE:
se uno o entrambi i limiti non sono finiti valgono le seguenti relazioni:
• per i risultati valgono le regole del quoziente
l1 = +∞, l2 = positivo, finito → l1 ÷ l2 = +∞
l1 = −∞, l2 = positivo, finito → l1 ÷ l2 = −∞
l1 = finito, l2 = ∞ → l1 ÷ l2 = 0 la divisione tra un numero finito e un numero sempre più grande tende
a zero
∞
0
l1 = l2 = ∞, → l1 ÷ l2 =
oppure l1 = l2 = 0, → l1 ÷ l2 = FORME INDETERMINATE
∞
0
•
FUNZIONE RECIPROCA :
1
1
=
f ( x) l
1
1
o se lim f ( x ) = 0 segue lim
= =∞
x → x0
x → x0 f ( x )
0
1
1
o se lim f ( x ) = ∞ segue lim
= =0
x → x0
x → x0 f ( x )
∞
o se lim f ( x ) = l segue lim
x → x0
x → x0
Le forme indeterminate esaminate sono :
1) + ∞ − ∞
2) 0 ⋅ ∞
∞
3)
∞
0
4)
0
Queste forme vanno risolte con particolari accorgimenti che permettono di eliminare le forme stesse
di indeterminazione.
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 9 di 13
FUNZIONE CONTINUA IN UN PUNTO E IN UN INTERVALLO
Sia f (x ) una funzione definita in un intervallo aperto ]a, b[ e sia x0 ∈ ]a, b[ .
La funzione è continua nel punto x0 se risulta
lim f ( x ) = f ( x0 )
x → x0
Per la definizione una funzione per essere continua deve rispettare le seguenti 3 condizioni:
A) esiste il valore della funzione nel punto x0 ;
B) esiste il limite della funzione nel punto x0 ;
C) limite e funzione nel punto x0 sono uguali .
Se la funzione è continua in un punto il calcolo del limite in tale punto risulta estremamente
semplificato in quanto basta calcolare il valore della funzione nel punto ed ottenerne il limite.
La funzione è continua in un intervallo se in tutto l’intervallo vale la relazione lim f ( x ) = f ( x0 ) .
x → x0
FUNZIONE CONTINUA A DESTRA : lim+ f ( x ) = f ( x0 )
x → x0
FUNZIONE CONTINUA A SINISTRA : lim− f ( x ) = f ( x0 )
x → x0
Una funzione continua è paragonabile ad una linea retta o a una curva ottenuta “senza alzare mai la
penna dal foglio”, non ci sono discontinuità nel tratto disegnato.
Esempi di funzioni discontinue:
Esempi di funzioni continue:
La funzione per x
tendente a zero assume
due valori
La funzione non
esiste nel punto 0
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 10 di 13
APPLICAZIONE DEI LIMITI ALLE FUNZIONE CONTINUE
Se la funzione è continua il calcolo del limite in un punto si riduce al calcolo della funzione nello
stesso punto ; in generale le funzioni sono continue in un intervallo tranne per alcuni valori come già
verificato nel calcolo del campo di esistenza di una funzione , valgono pertanto le seguenti
considerazioni:
1°. lim h = h , il limite di una costante è la costante stessa;
lim 3 = 3
x →1
x → x0
2°. lim x = x0 , il limite della variabile x è il valore della funzione nella variabile stessa; lim x = 1
x →1
x → x0
3°. se lim f ( x ) = l → lim [ f ( x )] = l il limite della potenza è uguale alla potenza del limite; se
n
x → x0
n
x → x0
lim x = 2 → lim[x ] = 23 = 8
3
x→2
x→2
4°. lim f ( x ) = l → lim
x → x0
n
x → x0
[ f ( x )] = n l
con n dispari , se n è pari il limite deve essere non negativo
l ≥ 0 , il limite della radice è uguale alla radice del limite.
5°. lim f ( x ) = l → lim log a f ( x ) = log l , il limite del logaritmo è uguale al logaritmo del limite;
x → x0
x → x0
a
lim( x + 1) = 3 → lim log a ( x + 1) = log 3
x→2
x→2
6°. lim f ( x ) = l → lim a
x → x0
a
f ( x)
x→ x0
= a , il limite della funzione esponenziale è uguale all’esponenziale del
l
limite;
+ ∞, a > 1
7°. lim f ( x ) = +∞ → lim a f ( x ) =
x → x0
x → x0
0,0 < a < 1
1
1
1
1
lim+
= +∞ → lim+ 2 x −1 = +∞ , lim−
= −∞ → lim− 2 x −1 = 0
x →1 x − 1
x →1
x →1 x − 1
x →1
RISOLUZIONE DELLE FORMA INDETERMINATA
;
∞−∞
PRIMO CASO : funzione razionale intera lim ax n + bx n −1 + ...k , messa in evidenza della variabile
x→∞
5 3
5
con esponente maggiore . Esempio: lim (2 x 3 − 5 x 2 + 3 x − 5) = lim x 3 ⋅ 2 − + 2 − 3 i limiti
x → −∞
x → −∞
x x
x
3
delle tre frazioni tendono a zero per il teorema della funzione reciproca e pertanto lim x ⋅ (2 ) = −∞ .
x → −∞
Come regola pratica il limite per x tendente all’infinito di una funzione razionale intera è uguale
all’infinito con segno uguale al prodotto dei segni tra il coefficiente della variabile di grado maggiore
e il segno assunto dalla stessa variabile per x → ±∞ .
SECONDO CASO : somma di funzioni irrazionali intere lim f ( x ) − g ( x ) , si razionalizzerà il
x→∞
(
)
(a + b) ⋅ (a − b ) = a 2 − b2 . Esempio:
(x + 1) − (x + 3) = 0 in quanto
x + 3)
= lim
numeratore mediante la regola del prodotto notevole
(
)
(
)(
x +1 − x + 3 ⋅ x +1 +
x +1 + x + 3
il numeratore è un numero e il denominatore tende a ∞ .
lim
x → +∞
x + 1 − x + 3 = lim
x → +∞
(
)
x → +∞
(
x +1 + x + 3
)
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 11 di 13
RISOLUZIONE DELLE FORMA INDETERMINATA
0
0
e
∞
∞
Entrambe le forme derivano dalle funzioni razionali fratte.
Nella prima entrambi i polinomi, numeratore e denominatore , si annullano per lo stesso valore a cui
tende il limite, essi pertanto sono scomponibili per lo stesso fattore che nei passaggi successivi può
essere semplificato in modo da eliminare la forma indeterminata.
Esempi:
x2 − 1 0
= ; scomponendo il numeratore ( differenza di quadrati, prodotto somma per differenza )
lim
x →1 x − 1
0
(x + 1) ⋅ (x − 1) e semplificando il fattore comune (x-1) lim(x + 1) = 2
x2 − 1
si avrà lim
= lim
x →1 x − 1
x →1
x →1
x −1
x 2 − 3x + 2 0
= , scomponendo il trinomio ax 2 + bx + c = a (x − x1 ) ⋅ ( x − x2 ) con x1 e x2 soluzioni
lim
x→2
x−2
0
(x − 1) ⋅ (x − 2 ) = lim( x − 1) = 1 .
x 2 − 3x + 2
dell’equazione di secondo grado si avrà lim
= lim
x→2
x→2
x→2
x−2
x−2
Nella seconda forma indeterminata occorre mettere in evidenza, sia a numeratore che a
denominatore, la variabile di grado maggiore, semplificare e risolvere il limite .
Esempi:
2
5
2
5
x 3 ⋅ 1 − 2 + 3
x ⋅ 1 − 2 + 3
3
3
x − 2x + 5 ∞
x − 2x + 5
x
x
x
x
lim
= ; lim
= lim
= lim
= +∞
2
2
x → +∞
x
→
+∞
x
→
+∞
x
→
+∞
1
1
x −1
∞
x −1
2
x ⋅ 1 − 2
1 − 2
x
x
2
5
x 3 (2 − 2 + 3 )
2x3 − 2x + 5 ∞
2x3 − 2x + 5
x
x = 2=2
lim
= ; lim
= lim
3
3
x → +∞
x → +∞
1
x −1
∞ x → +∞
x −1
1
x 3 ⋅ (1 − 3 )
x
2
5
x 3 (2 − 2 + 3 )
2x3 − 2x + 5 ∞
2x3 − 2x + 5
x
x = lim 1 = 0
lim
= ; lim
= lim
4
4
x → +∞
x → +∞
x → +∞ x
1
x −1
∞ x → +∞
x −1
x 4 ⋅ (1 − 4 )
x
Praticamente , per individuare il risultato immediatamente vale la seguente regola:
si individuano i gradi del polinomio a numeratore n e del polinomio a denominatore p ;
se n > p grado numeratore maggiore del grado del denominatore, il limite vale infinito;
se n = p numeratore e denominatore hanno lo stesso grado, il limite è finito ed è uguale al
rapporto dei rispettivi coefficienti dei termini di grado maggiore ;
se n < p grado numeratore minore del grado del denominatore, il limite è finito e vale zero.
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 12 di 13
FORMA INDETERMINATA 1∞
x
1
∞
LIMITE NOTEVOLE lim 1 + = 1 forma indeterminata
x → +∞
x
x
1
Si può dimostrare che il limite della forma indeterminata 1 è uguale a e : lim 1 + = e
x → +∞
x
∞
il numero e , numero irrazionale con valore approssimato e ≈ 2,71828... è utilizzato spesso come
base dei logaritmi .
Esempio: lim (1 + x ) x il limite è una forma indeterminata del tipo 1∞ ; per applicare il limite notevole
1
x→0
è opportuno effettuare il cambio di variabile x =
1 1
; = y , inoltre al tendere della x a zero la
y x
x → 0
variabile y deve tendere a più infinito
; operando le trasformazioni il limite diventa:
y → +∞
lim(1 + x )
x→0
1
x
y
1
= lim 1 + = e
y → +∞
y
DISCONTINUITÀ DI UNA FUNZIONE
Sia f (x ) una funzione definita in un intervallo ]a, b[ ; considerato un punto x 0 ∈ ]a, b[ , la funzione
è discontinua nel punto x0 se essa non è continua in x0 . Il punto x0 si chiama punto singolare o di
discontinuità .
CLASSIFICAZIONE DEI PUNTI DI DISCONTINUITÀ:
PRIMA SPECIE: nel punto x0 esistono e sono finiti i limiti destro e sinistro e sono diversi tra loro;
SECONDA SPECIE: nel punto x0 non esiste uno dei due limiti sinistro e destro oppure almeno uno
di questi limiti è infinito;
TERZA SPECIE: esiste il limite nel punto x0 ma il valore della funzione o non esiste in x0 oppure
esiste ma risulta diverso dal limite .
Esempio prima specie: y = x +
x
x
x
1
-1
2
-2
0,05
-0,05
x
= −1
x→0
x
x
lim+ = x + = +1
x→0
x
lim− = x +
Esempio seconda specie: y = 2
Esempio terza specie: y =
1
x
f(x)
1
x
lim+ 2 = 2
x→0
1
lim ( )
x
x →0+
2
-2
3
-3
1,05
-1,05
=2
+∞
= +∞
1
x
lim− 2 = 2
x→0
1
lim ( )
x
x→ 0 −
= 2− ∞ = 0
x2 − 1
nel punto x=1 non esiste la funzione ma esiste il limite.
x −1
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
LIMITI
Pagina 13 di 13










