Teorie sull’atomo: sviluppo storico
1834 M.Faraday: la materia è costituita da particelle cariche
elettricamente.
1897 J.J.Thomson: determinazione del rapporto e/m
(carica/massa) per l’elettrone (sempre lo stesso
nonostante la provenienza degli elettroni).
1909 R.A.Millikan: carica dell’elettrone.
Modello di Thomson 1904
Carica positiva distribuita in modo uniforme, ed elettroni
localizzati all’interno dell’atomo in posizioni di equilibrio.
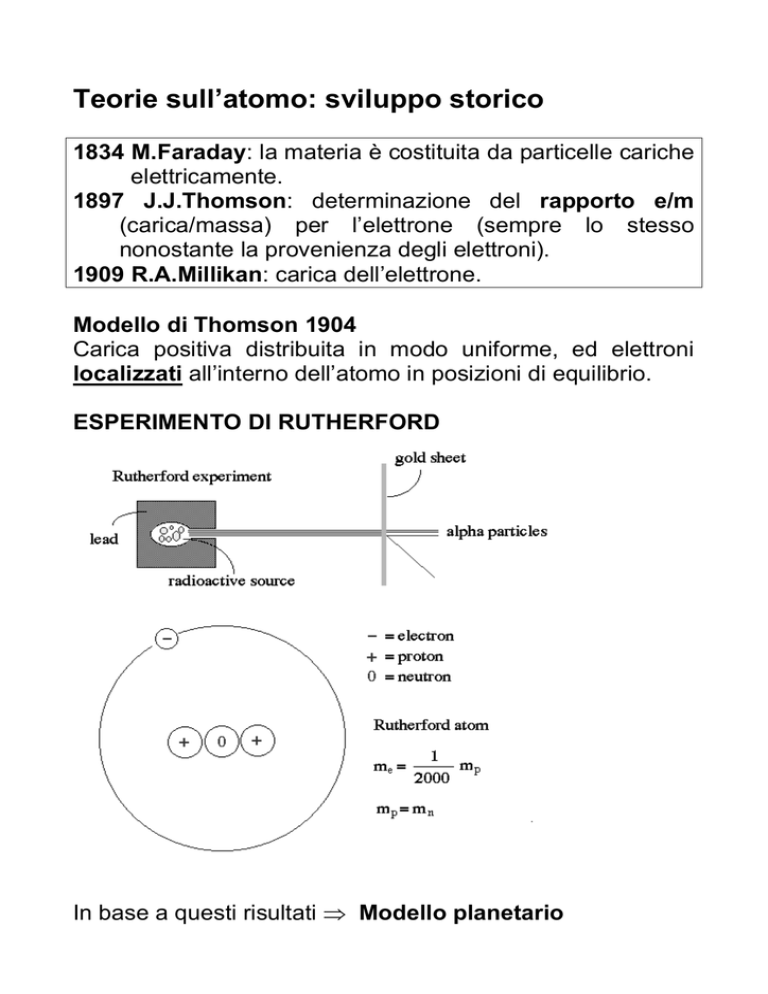
ESPERIMENTO DI RUTHERFORD
In base a questi risultati ⇒ Modello planetario
Modello planetario
1. Tutta la carica positiva e
quasi tutta la massa sono
concentrate nel nucleo.
2. Gli
elettroni
orbitano
intorno
al
nucleo,
in
posizioni di equilibrio, ovvero:
3. Forza centrifuga mv2/r = attrazione
elettrostatica q1q2/r2
4. Problema: secondo la fisica classica,
ruotando intorno al nucleo, l’elettrone
emetterebbe radiazioni, perdendo così energia
e collassando rapidamente.
Modello di Bohr
dell’atomo
di
idrogeno (1913)
E’ il risultato
dell’applicazione al
modello planetario
della teoria dei
quanti di Planck.
Idea di Bohr
Sono possibili solo le orbite “stazionarie” per
le quali:
r = a0.n2 con a0=0.53 Å n=1,2,3,…
2π2me4
E= E(n)= - _____ *__________
n2
h2
1
(h/2π) = ®
n è detto numero quantico.
Vantaggi e svantaggi
1. Il modello di Bohr spiega molto bene lo
spettro dell’atomo di idrogeno e degli
idrogenoidi (dati sperimentali).
2. Per essere applicabile ad atomi
polielettronici ha dovuto essere adattato
progressivamente.
3. Inoltre è stato ottenuto con la teoria della
fisica classica, che non ammette a priori le
orbite stazionarie.
Teoria ondulatoria
1-Principio di indeterminazione
Heisenberg (1926)
• Non è possibile descrivere con esattezza
la traiettoria di una particella elementare
(es. elettrone intorno al nucleo).
• Se ad esempio vogliamo conoscere
velocità v e posizione x di una particella,
avremo:
Δ x*Δp= Δ x*Δv*m ú costante (h/2π)
2-Onda associata di De Broglie (1923)
Ad una particella di massa m che si muove
nello spazio con velocità v è associata
un’onda con
λ=h/mv.
(Applicazione: il microscopio elettronico)
EQUAZIONE DI SCHRÖDINGER
1. Il moto dell’elettrone nel campo del
nucleo si descrive con una equazione
d’onda
2. Le soluzioni delle equazioni d’onda
applicate all’elettrone sono chiamate
funzioni orbitali o più semplicemente
orbitali.
FUNZIONI D’ONDA Ψ
Dipendono da tre numeri quantici n, l, m
Ψ= Ψ(n,l,m)
n = numero quantico principale
n=1,2,3,..
Compare già nel modello di Bohr
Dal valore di n conseguono i valori possibili
degli altri parametri.
l = numero quantico
azimutale o angolare.
valori interi 0≤ l ≤ n-1
secondario
o
m = numero quantico magnetico
valori interi - l ≤ m ≤ + l
Considerazioni
1. ad ogni orbitale corrisponde (“è
associato”) un dato valore di energia.
2. per l’atomo di idrogeno E=E(n).
3. per atomi con almeno due elettroni
E=E(n,l).
4. orbitali con lo stesso valore di E sono
detti degeneri.
5. Per un atomo polielettronico, ciò significa
che hanno gli stessi valori di n ed l, (per
idrogeno od idrogenoidi, è sufficiente n).
n=1 ⇒ l =? m=?
l = 0….n-1= 0
m= -l ….0…+l = 0
la funzione orbitale è Ψ100 ⇒ orbitale 1s
n=2 ⇒ l =? m=?
l = 0….n-1= 0,1
m= -l ….0…+l = -1,0,+1
n
2
2
l
0
1
m
Ψ
0
Ψ200 orbitale 2s
Ψ21-1 Ψ210 Ψ211 orbitali 2p
1,0,1
n=3⇒ l =? m=?
l = 0….n-1= 0,1,2
m= -l ….0…+l = -2,-1,0,+1,+2
n
3
3
3
l
0
1
2
m
0
-1,0,1
-2,-1,0,
+1,+2
Ψ
Ψ300
orbitale 3s
Ψ31-1 Ψ310 Ψ311 orbitali 3p
Ψ32-2 Ψ32-1 Ψ320 Ψ321 Ψ322
orbitali 3d
• In assenza di campo magnetico il valore
dell’energia dipende solo dai numeri
quantici n ed l
• Il numero quantico l si sostituisce
solitamente con una lettera:
l =0 l =1 l =2 l =3
s
p
d
f
Da questa simbologia
nomenclatura più diffusa:
discende
la
Ψ100 ⇒ Ψ10 ⇒10 ⇒1s
Ψ200 ⇒ Ψ20 ⇒20 ⇒2s
Definizioni
• Livelli energetici: orbitali con egual
valore di n (ev. diverso l) appartengono
allo stesso livello energetico.
• Sottolivelli: se gli orbitali hanno anche
lo stesso l sono nello stesso sottolivello
di energia.
energia
energia
3s
3p
3d
Atomo di idrogeno e
atomi idrogenoidi
3d
3p
3s
Atomi polielettronici
E gli elettroni?
• Una “funzione orbitale” può descrivere
al massimo il comportamento di due
elettroni.
• Questi differiscono fra loro per il quarto
numero quantico: lo spin:
ms=-½
ms=+½
(la teoria classica interpreta lo spin come
rotazione dell’elettrone su se stesso,
mentre ruota attorno al nucleo).
Principio di esclusione di Pauli (1925)
1. In un atomo non possono esistere due
elettroni con i quattro numeri quantici
uguali.
2. Tre numeri quantici
individuano
l’orbitale, il quarto gli elettroni ⇒ non
più di due elettroni per orbitale.
Rappresentazione nello spazio degli
orbitali
L’equazione di Schrödinger permette di
calcolare la densità elettronica nello
spazio, cioè la probabilità di trovare
l’elettrone in un “orbitale” in funzione del
raggio r e della direzione.
Impropriamente,
dell’orbitale.
forma
e
dimensione
Orbitale 1s per l’atomo di idrogeno
1. funzione d’onda
2. probabilità (per unità di volume) in
funzione di r
3. probabilità radiale in funzione di r
(Ψ2dV, con dV=4πr2dr)
probabilità
Funzione
d’onda
Probabilità
radiale
• la distanza r = 0.53 Å è la stessa
dell’atomo di Bohr, ma qui è la distanza
a cui si ha la massima probabilità di
trovarlo.
• La curva di probabilità radiale ci
fornisce la probabilità di trovare
l’elettrone in funzione della distanza dal
nucleo ⇒ ≈forma dell’orbitale.
Superfici di equiprobabilità
• Si ottengono congiungendo i punti dello
spazio con lo stesso valore di
probabilità
(vale
in
generale!).
• Per gli orbitali 1s si
ottengono delle sfere
concentriche.
• In genere si riportano le
intersezioni con il piano
xy, con l’aspetto di cerchi
concentrici.
Nuvola elettronica
La densità dei punti nello spazio è
proporzionale a Ψ2
Superfici limite
• Prendendo in esame le superfici di
equiprobabilità, si evidenzia e si
disegna la più piccola entro cui si ha il
90% di probabilità di trovare l’elettrone.
• Vale a dire, per un tempo abbastanza
lungo, l’elettrone trascorrerà il 90% del
tempo nello spazio delimitato dalla
superficie.
Orbitali 2s , 3s, ed oltre
• Per 2s si ha uno zero della curva di
probabilità. Per 3s se ne hanno due.
• Ogni zero della curva genera una
superficie nodale, cioè una zona in cui
la probabilità di trovare l’elettrone è
zero.
• Per 2s e 3s abbiamo, rispettivamente,
uno e due sup. nodali (“gusci” vuoti).
• Per gli orbitali s la superficie limite è
sempre una sfera di raggio crescente
con n.
Per un orbitale s, il numero di superfici nodali è n-1
Orbitali p (l=1)
Ψ211= Ψ210 = Ψ 21-1 ⇒ 2p
• Simmetria rispetto ad un asse, non ad
un punto come per gli orbitali s.
• Superficie limite: descrive figura “a
“doppia clava” formata da due lobi, fra
di loro tangenti in corrispondenza del
nucleo.
• Nomi: se, ad es., un orbitale p è
simmetrico rispetto all’asse z è detto pz.
• Il piano xy, che separerà i due lobi, è un
piano nodale.
• Gli altri due orbitali px e py sono orientati
secondo gli altri due assi.
2px , 2py , 2pz ⇒ 2p
• Gli orbitali 3p sono anch’essi figure a
due lobi, più grandi, e con in più una
superficie nodale (oltre al piano nodale).
• Il numero delle superfici nodali si ricava
dalla formula n-l-1
Orbitali 3d
l=2
m=-2,-1,0,+1,+2
⇓
sono 5 orbitali degeneri (“isoenergetici”)
sup.nod.= n-l-1
Riepilogo sui numeri quantici
Numero quantico principale n
• Individua energia
e dimensioni
dell’orbitale (con l’aumentare di n,
aumentano le dimensioni).
• Insieme ad l determina il numero delle
superfici nodali.
Numero quantico secondario l
• Influisce su energia (sottolivello) e sul
numero delle superfici nodali.
• Individua la forma dell’orbitale (l=0 ⇒
s, l=1⇒d) ed il numero dei piani nodali.
Numero quantico magnetico m
• Orientazione nello spazio dell’orbitale
(numero degli orbitali degeneri).
energia
energia
Ordine di riempimento degli orbitali
3s
3p
3d
Atomo di idrogeno e
atomi idrogenoidi
3d
3p
3s
Atomi polielettronici
Configurazione elettronica di un
elemento: la disposizione degli elettroni
negli orbitali.
L’ordine di riempimento degli orbitali
dipende da questa successione delle
energie:
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p <
5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s <
6d< 5f
La configurazione elettronica si determina
coi segg. criteri:
1. un elettrone occupa l’orbitale a cui
corrisponde lo stato di minore energia.
2. un orbitale può essere occupato al più
da due elettroni (Pauli).
3. Criterio di Hund (minima energia,
1927)
…
vuoto
m.
mo
semipieno
pieno
• Gli elettroni si sistemano negli orbitali
degeneri collocando dapprima un
elettrone per orbitale, con spin paralleli.
• Il secondo elettrone si aggiunge solo
quando tutti gli orbitali degeneri sono
semipieni.
Corretta
Scorretta
m :: …
2p1
m m …
2p2
m m m
2p3
mo m m
2p4
mo mo m
2p5
mo mo mo
2p6
mo …. …
NON 2p2
mo m.. ...
NON 2p3
mo mo …
NO..2p4
Z=1 Idrogeno (H)
1s1
Z=2 Elio (He)
1s2
1° Periodo
2° Periodo
2s
2
1
[He]2s
2p
1
Z=3 Litio (Li)
1s 2s
Z=4 Berillio (Be)
1s22s2
Z=5 Boro (B)
1s22s22p1 [He]2s22p1
Z=6 Carbonio (C)
1s22s22p2 [He]2s22p2
Z=7 Azoto (N)
1s22s22p3 [He]2s22p3
Z=8 Ossigeno (O)
1s22s22p4 [He]2s22p4
Z=9 Fluoro (F)
1s22s22p5 [He]2s22p5
Z=10 Neon (Ne)
1s22s22p6 [He]2s22p6
[He]2s2
3° Periodo
3s
Z=11 Sodio (Na)
2
2
6
1s 2s 2p 3s
1
Z=12 Magnesio (Mg)1s22s22p63s2
[Ne]3s
1
[Ne]3s2
Z=13 Alluminio (Al) 1s22s22p63s23p1 [Ne]3s23p1
Z=14 Silicio (Si)
1s22s22p63s23p2 [Ne]3s23p2
Z=15 Fosforo (P)
1s22s22p63s23p3 [Ne]3s23p3
Z=16 Zolfo (S)
1s22s22p63s23p4 [Ne]3s23p4
Z=17 Cloro (Cl)
1s22s22p63s23p5 [Ne]3s23p5
Z=18 Argon (Ar)
1s22s22p63s23p6 [Ne]3s23p6
3p
1° , 2°, 3° periodo comprendono solo
elementi tipici o rappresentativi, cioè quelli
con elettrone discriminante s o p.
4°periodo
1
K
[Ar] 4s
Ca [Ar] 4s2
Gli elementi da Sc a Zn (elettrone
discriminante d)
[Ar] 3d1-10 4s2
(Prima serie di transizione)
Configurazioni anomale: Cr e Cu
Cr atteso [Ar] 3d4 4s2
Cr stabile [Ar]3d5 4s1
Cu atteso [Ar] 3d9 4s2
Cu stabile [Ar]3d10 4s1
orbitali pieni o semipieni ⇒ configurazioni
elettroniche più stabili.
4 periodo-continua
Ga d Kr riempimento degli orbitali 4p
dopo l’interruzione della 1° serie di
transizione.
[Ar] 3d10 4s2 4p1-6
(Il V periodo è analogo al IV)
6°periodo
• Con La= [Xe] 5d1 6s2 d (III serie di
transizione), interrotta dai:
• Lantanidi CedLu, a configurazione
[Xe]4f2-14 5d0 6s1
(I serie interna di transizione)
• Riprende poi la III serie di transizione
14
2-10
2
HfdHg =[Xe]4f 5d 6s
• Con Tallio Tl si riprende la serie degli
elementi tipici (orbitali 6 p)
7°periodo
Inizia con Francio e Radio:
Fr
[Rn]7s1
Ra [Rn]7s2
Con Attinio Ac comincia la IV serie di
transizione
Ac= [Rn]6d17s2
E’ seguito dagli altri attinidi Th-Lw
[Rn] 5f2-14 6d0(1)7s2
(II serie interna di transizione)
Osservazioni
• Terre rare = Sc, Y, La e lantanidi.
Nome ⇒ ragioni storiche.
Stessa struttura elettronica esterna
(elettroni di valenza) d analoga reattività.
• Idrogeno: si può sistemare sia in IA che
in VII A. Infatti può perdere un elettrone
+
per trasformarsi in H (dIA), ma anche a
completare l’orbitale (dVIIA)
Periodi e riempimento degli orbitali
Periodo nome
1
2
3
4
5
6
7
primo
piccolissimo
periodo
primo piccolo
periodo
secondo
piccolo
periodo
primo grande
periodo
secondo
grande
periodo
primo
grandissimo
periodo
secondo
grandissimo
periodo
Numero
elettroni
2
orbitali
1s2
8
2s2 2p6
8
3s2 3p6
18
4s2 4p6 3d10
18
5s2 5p6 4d10
32
6s2
6p6
5d104f14
incompleto 7s2 7p0 6d1
5f14
Struttura elettronica e gruppi
IA
II A
III A
IV A
VA
VI A
VII A
0
alcalini
[ ]ns1
alcalino- [ ]ns2
terrosi
terrosi
[ ]ns2np1
[ ] ns2np2
[ ] ns2np3
calcogeni [ ] ns2np4
alogeni [ ] ns2np5
gas nobili [ ] ns2np6
Es. Na+
Es. Be2+
Es.Al3+
Es. O2Es. F-
Abbreviazioni per gli elementi tipici
Quando scriviamo [ ] per un elemento
del blocco s, corrisponde a: Gas Inerte
Quando scriviamo [ ] per un elemento
del blocco p, corrisponde a:
2,3 periodo⇒ Gas Inerte (G.I.)
4,5 periodo⇒ G.I., (n-1)d10
6 periodo ⇒ G.I., (n-2)f14(n-1)d10












