Didasfera - Ambiente didattico digitale
2.2.2 Il contenuto geometrico degli Elementi
Mappa dell'Unità
Mappa dell'Unità
Due triangoli sono congruenti se hanno congruenti tutti i lati e tutti gli angoli. Esistono alcuni teoremi chiamati criteri di
congruenza che permettono di confrontare solo alcuni lati e/o angoli per essere comunque sicuri che due triangoli siano
effettivamente congruenti.
Teorema - I criterio di congruenza dei triangoli
Se due triangoli hanno ordinatamente congruenti due lati e l'angolo compreso tra essi allora i due triangoli sono
congruenti.
Pagina 1/3
Didasfera - Ambiente didattico digitale
I criterio di congruenza.
DIMOSTRAZIONE
Si sovrappone il segmento AB al segmento DE, il segmento BC al segmento EF e l'angolo `AhatBC`, all'angolo
`DhatEF`. Tale sovrapposizione è possibile perché per ipotesi questi lati e l'angolo compreso sono congruenti. Allora il
vertice A risulta sovrapposto al vertice D e il vertice C risulta sovrapposto al vertice F. Avendo tutti i vertici sovrapposti i
due triangoli sono congruenti.
Tale dimostrazione è quella originale di Euclide, ma secondo la matematica moderna tale metodo di dimostrazione non
è più considerato accettabile. Il I criterio di congruenza è stato inserito da Hilbert tra i suoi postulati.
Teorema - II criterio di congruenza
Se due triangoli hanno congruenti due angoli e il lato compreso tra essi allora i due triangoli sono congruenti.
Teorema - III criterio di congruenza
Se due triangoli hanno congruenti i tre lati allora sono congruenti.
Nei triangoli rettangoli si è già certi che c'è un angolo congruente, ed è quello retto. E' possibile quindi trovare criteri di
congruenza più semplici dei tre criteri precedenti.
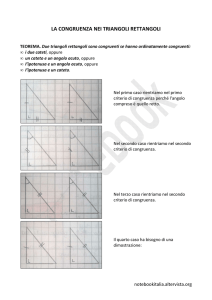
I criterio: se due triangoli rettangoli hanno congruenti i due cateti allora sono congruenti.
II criterio: se due triangoli rettangoli hanno congruenti un cateto e l'angolo acuto opposto allora sono congruenti.
III criterio: se due triangoli rettangoli hanno congruenti un cateto e l'angolo acuto adiacente allora sono congruenti.
IV criterio: se due triangoli rettangoli hanno congruenti l'ipotenusa e un angolo acuto allora sono congruenti.
V criterio: se due triangoli rettangoli hanno congruenti l'ipotenusa ed un cateto allora sono congruenti.
Teorema (dell'angolo esterno di un triangolo)
Ogni angolo esterno di un triangolo è maggiore di ciascuno degli angoli interni non adiacenti.
DIMOSTRAZIONE
Si consideri M punto medio di AB. Si tracci un segmento ME sulla semiretta CM tale che `CM~=ME` e CM non sia
sovrapposto a ME. I triangoli AME e CMB sono congruenti per il primo criterio avendo gli angoli in M congruenti in
quanto opposti, `CM~=ME` per costruzione e `AM~=MB` in quanto M punto medio. Da ciò segue che l'angolo
`EhatAM~=MhatBC`. Ma `EhatAM~=DhatAM` da cui la tesi.
Pagina 2/3
Didasfera - Ambiente didattico digitale
In questa unità
Testo: Storia delle idee
Autore: Marcello Ciancio
Curatore: Maurizio Châtel
Metaredazione: Rosanna Lo Piccolo
Editore: BBN
Pagina 3/3