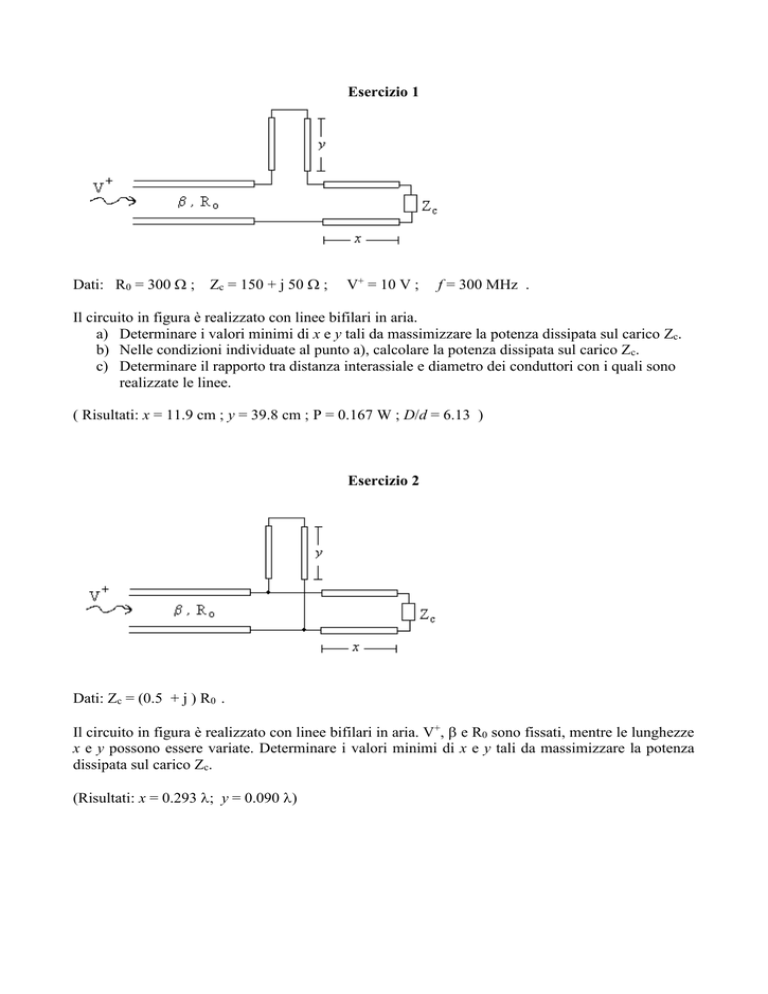
Esercizio 1
Dati: R0 = 300 ; Zc = 150 + j 50 ;
V+ = 10 V ;
f = 300 MHz .
Il circuito in figura è realizzato con linee bifilari in aria.
a) Determinare i valori minimi di x e y tali da massimizzare la potenza dissipata sul carico Zc.
b) Nelle condizioni individuate al punto a), calcolare la potenza dissipata sul carico Zc.
c) Determinare il rapporto tra distanza interassiale e diametro dei conduttori con i quali sono
realizzate le linee.
( Risultati: x = 11.9 cm ; y = 39.8 cm ; P = 0.167 W ; D/d = 6.13 )
Esercizio 2
Dati: Zc = (0.5 + j ) R0 .
Il circuito in figura è realizzato con linee bifilari in aria. V+, e R0 sono fissati, mentre le lunghezze
x e y possono essere variate. Determinare i valori minimi di x e y tali da massimizzare la potenza
dissipata sul carico Zc.
(Risultati: x = 0.293 ; y = 0.090 )
Esercizio 3
Dati:
l 0.25 2 m;
Vg = 10 V ;
R0 = 50 ; Rg = 10 ;
f = 300 MHz ;
Zc = 10 + j 40 ;
r = 2 .
Il circuito in figura è realizzato con cavi coassiali (r = 2, perdite trascurabili).
a) Determinare i valori minimi di x e y tali da massimizzare la potenza dissipata sul carico Zc.
b) Nelle condizioni individuate al punto a), calcolare la potenza dissipata sul carico Zc.
c) Determinare il rapporto tra diametro della calza esterna e diametro del conduttore interno
per i cavi coassiali con i quali sono realizzate le linee.
( Risultati: x = 8.84 cm ; y = 20.4 cm ; P = 1.25 W ; D/d = 3.25 )
Esercizio 4
Dati: R0 = 50 ;
Vg = 5 V ;
Rg = 50 ;
f = 3 GHz ;
Zc = 150 + j 50 ;
r = 3 ;
h = 1 mm .
Il circuito in figura è realizzato con microstrisce (h = 1 mmr = 3, t 0, perdite trascurabili).
a) Determinare la larghezza W della striscia metallica e calcolare eff.
b) Determinare i valori minimi di x e y tali da massimizzare la potenza dissipata sul carico Zc.
c) Nelle condizioni individuate al punto b), calcolare la potenza dissipata sul carico Zc.
( Risultati: W = 2.51 mm ; eff = 2.42 ; x = 12.0 mm ; y = 6.71 mm ; P = 0.0625 W ).
Esercizio 5
Dati: R0 = 100 ; Rg = 50 ;
Vg = 10 V ; f = 3 GHz ;
Ra = 100 ; Zc = 50 ;
r = 4 ;
l = 1.25 cm ; b = 1 cm .
Il circuito in figura è realizzato con stripline (b = 1 cmr = 4, t 0, perdite trascurabili).
a) Determinare la larghezza W della striscia metallica.
b) Determinare i valori minimi di x e y tali da massimizzare la potenza dissipata sul carico Zc.
c) Nelle condizioni individuate al punto b), calcolare la potenza dissipata sul carico Zc.
( Risultati: W = 0.095 cm ; x = 0.27 cm ; y = 1.74 cm ; P = 0.083 W ).
Esercizio 6
Dati: Zc = 2 R0 , l = /8
Il circuito in figura è realizzato con linee bifilari in aria. Vg , ed R0 sono fissati, mentre le
lunghezze x e y possono essere variate. Determinare i valori minimi di x e y tali da massimizzare la
potenza trasferita al carico Zc.
(Risultati: x = ; y = )
Esercizio 7
Dati: Z0 = 50 ;
Vg = 10 V ;
Z1 = (1 + 2 j) Z0 ;
f = 100 MHz ;
Z2 = (1 + j) Z0 ;
l = 75 cm ;
P1 = 1/5 P2 .
Il circuito in figura è realizzato con linee bifilari in aria.
a) Calcolare il minimo valore di x tale che la potenza dissipata sul carico Z1 sia 1/5 di quella
dissipata su Z2, ed il minimo valore di y ed il valore di Z’ tali da massimizzare la potenza
complessivamente assorbita dai carichi Z1 e Z2.
b) Determinare, lungo il tratto di linea di impedenza caratteristica Z’, l’ascissa in
corrispondenza della quale il modulo della tensione assume valore massimo e calcolare il
valore di tale massimo.
(Risultati: x = 75 cm; y = 90 cm; Z’ = 61.2 ; z = 75 cm;
|V|max = 6.12 V)
Esercizio 8
l
Dati: l = 1.52 cm ;
l
r = 4;
Z0 = 50 (impedenza caratteristica del tratto vuoto)
La struttura risonante in figura è costituita da un tratto di cavo coassiale di lunghezza 2l chiuso alle
estremità da pareti di conduttore elettrico perfetto e riempito per metà con un mezzo avente costante
dielettrica relativa pari a 4.
a) Calcolare la frequenza fondamentale di risonanza.
b) Supponendo che nella struttura sia presente un campo elettromagnetico alla frequenza
fondamentale di risonanza, determinare la sezione in corrispondenza della quale la tensione
ha modulo massimo.
(Risultati: f0 = 3 GHz; la sezione richiesta è a 1.25 cm dalla parete terminale destra)
Esercizio 9
Tabella A
Diametro d del conduttore interno*
1.15 mm
Diametro D del conduttore esterno*
5.60 mm
Spessore del conduttore esterno*
0.5 mm
Permittività relativa del dielettrico
1.56
(parte reale)
Impedenza caratteristica R0
75
Capacità per unità di lunghezza C
54 pF/m
Induttanza per unità di lunghezza L
0.31 H/m
* Conduttori in rame
In Tabella A sono elencate le principali proprietà geometriche ed elettromagnetiche di un cavo
coassiale usato per collegare un apparecchio televisivo alle antenne per la ricezione di trasmissioni
nelle bande VHF e UHF.
Calcolare il coefficiente di attenuazione del cavo a 200 MHz e a 800 MHz, assumendo che la
conducibilità del rame sia pari a 5.8 .107 S/m e che la tangente di perdita del dielettrico sia pari a
5.10 ad entrambe le frequenze.
(Risultati:
a 200 MHz, =9.41 10 m, corrispondente ad una attenuazione di 0.082 dB/m;
a 800 MHz, =21.4 10 m, corrispondente ad una attenuazione di 0.185 dB/m)












