Simulazione prima prova parziale (III)
F.1) Cosa si può dire dell’accelerazione e delle forze che agiscono su un corpo che si muove di moto
circolare uniforme?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nei moti circolari uniformi, quali relazioni legano tra loro periodo, frequenza e velocità angolare?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Un’automobile viaggia alla velocità di 72 km/h.
Il raggio delle ruote è pari a 35 cm.
Sapendo che le ruote rotolano senza strisciare sull’asfalto, calcolare il numero di giri al secondo
della ruota
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Quanto valgono il periodo di rotazione e la velocità angolare di rotazione attorno ai semiassi per
quell’auto?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ris.: F~R = −mω 2~r; f =
v
2πr
= 9.1 giri/s;T = 0.11 s ω = 57.1 rad/s
F.2) Come si enuncia e quali sono le condizioni di applicabilità della legge di Poiseulle? Quale è il suo
significato dal punto di vista energetico?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
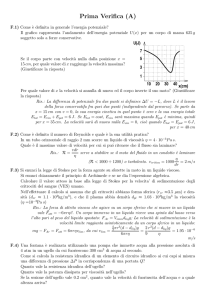
Due tubi rigidi orizzontali di raggio rispettivamente 2 mm e 1 mm, collegati come mostrato in
figura, vengono percorsi da una portata di 5 cm3 /s. Il liquido ha densità 0.8 g/cm3 e viscosità
3 · 10−3 P a s.
A
B C
D
0
5
10
Quanto vale la velocità media nei due tubi? Il flusso è laminare?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
X(cm)
Quanto vale la differenza di pressione PC − PD ?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spiegare perchè è possibile applicare il teorema di Bernoulli fra i punti B e C e poi lo si utilizzi
per calcolare PB − PC .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Sapendo che
PA − P B =
1
(PC − PD )
16
disegnare il grafico PA − P (x) della
pressione del liquido in funzione della
posizione x lungo il tubo.
v1 r1 d
Qd
Q
= 0.4 m/s; R1 =
=
= 213; v2 = 1.6 m/s; R2 = 417;
2
πr1
η
πr1 η
8ηL
1
PC − P D =
Q = 1900 P a; PB − PC = d(vC2 − vB2 ) = 960 P a;
4
πr
2
x
P (x) (Pa) PA − P (x) (Pa)
A
PA
0
1
B PA − 16 1900 = PA − 120
120
C
PB − 960 = PA − 1080
1080
D PC − 1900 = PA − 2980
2980
F.3) Un sacchetto di plastica sottile, facilmente deformabile, pieno di aria a pressione ambiente viene
accuratamente chiuso e sigillato.
Lo si porta poi in mare a 10 m di profondità dove il suo volume si adatta alla nuova pressione.
Si dica quanto valgono la pressione assoluta, la pressione transmurale e la pressione relativa
dell’aria nel sacchetto a tale profondità.
Ris.: v1 =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ris.: Sacchetto deformabile quindi sempre Pint = Pest .
= Pest = Patm + dgh = 1.99 · 105 P a; Pt = Pint − Pest = 0;
Prel = Pass − Patm = dgh = 9.8 · 104 P a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Pass
F.4) Quanto vale (espresso in Pascal), il modulo di Young di un elastico lungo 2 m e di sezione 25 mm 2
che si allunga di 5 cm quando sorregge una massa di 5 Kg?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1F
F L
∆L
=
quindi Y =
= 7.8 · 107 P a
L
Y S
S ∆L
F.5) Calcolare la forza di Archimede che agisce su una bollicina di CO2 di raggio 0.5 mm formatasi
al fondo di un bicchiere di acqua gassata. (si considerino trascurabili la densità della bollicina e
la differenza di pressione dovuta al livello di acqua nel bicchiere)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ris.:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Si enunci la legge di Stokes per la forza agente su sferette in moto in un liquido viscoso e la si
applichi per calcolare le velocità limite con cui la bollicina sale verso l’alto.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
Ris.: FAr = Vimm dliq g = πr 3 dg = 5.1 · 10−6 N ; asintoticamente FAr = Fatt = 6πrηvlim ;
3
FAr
2 r 2 dg
vlim =
=
= 54 cm/s
6πrη
9 η
F.6) Cosa afferma il teorema dell’energia cinetica (detto anche “delle forze vive”)?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Il grafico rappresenta l’andamento dell’energia cinetica Ecin (x) per un corpo di massa 625 g che
si muove sotto l’azione di un campo elettrico.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Quanto vale il lavoro compiuto dalle forze elettriche quando
l’oggetto si sposta da x = 30 cm a x = 70 cm?
Ecin
(J)
0.25
0.20
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0.15
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0.10
30 40 50 60 70 X(cm)
Quanto vale la differenza di energia potenziale fra questi due punti? In quale punto si ha energia
potenziale maggiore?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
f in
in
Ris.: L = ∆Ecin = Ecin
− Ecin
= 0.10 J; ∆U = −L = −0.10 J. L’energia potenziale
diminuisce, è maggiore in x = 30 cm (dove l’energia cinetica è minore)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .