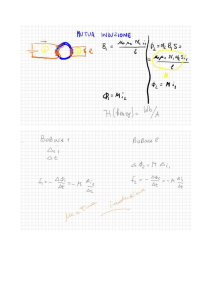
Elettromagnetismo
quasi stazionario
www.die.ing.unibo.it/pers/mastri/didattica.htm
(versione del 20-10-2012)
Effetti capacitivi e induttivi associati a un circuito
● Sulla superficie di un conduttore percorso da corrente è presente
una distribuzione superficiale di carica
Alla superficie del conduttore si appoggiano dei tubi di flusso di D
sulle cui sezioni terminali si localizzano cariche uguali e opposte
Questi tubi di flusso costituiscono
dei condensatori elementari
● La corrente nel circuito genera
un campo magnetico
Un circuito elettrico è sempre
concatenato con tubi di flusso di B
i
B
D
2
Effetti capacitivi e induttivi associati a un circuito
● In condizioni stazionarie è possibile studiare il campo di corrente
prescindendo dalla presenza di un campo elettrico e di un campo
magnetico all’esterno del conduttore
● Noti il potenziale e la corrente nel conduttore si possono determinare
il campo magnetico e la distribuzione della carica sulla superficie
i
● In condizioni non stazionarie
le equazioni che governano il
campo elettrico e il campo magnetico all’esterno del conduttore
sono accoppiate con le equazioni
del campo di corrente
In queste condizioni il comportamento
del circuito è influenzato anche dalla
presenza di effetti induttivi e capacitivi
B
D
3
Elettromagnetismo stazionario - riepilogo
J
Q
B
Ei
Legge di
Hopkinson
D
Q
H J
Β 0
B H
E 0
J 0
E 0
D 0
J ( E E i )
D E
R iC
Legge
Ri e
di Ohm
Q
Equazione del
V
condensatore
C
4
Elettromagnetismo stazionario - riepilogo
● Resistenza
RAB
V
AB
i
● Riluttanza
R AB
Edl
AB
JdS
l
dx
( x) A( x)
0
S
Hdl
dx
AB AB
BdS 0 ( x) A( x)
● Capacità
l
S
Edl
l
V
1
dx
AB AB
C AB
Q
DdS 0 ( x) A( x)
Le ultime uguaglianze
valgono nel caso di
tubi di flusso “filiformi”
S
5
Induttori e condensatori
● Normalmente i circuiti elettrici sono realizzati in modo che gli effetti
induttivi e capacitivi siano significativi solo all’interno di determinate
regioni che corrispondono a componenti detti induttori e condensatori
Proprietà che a rigore dovrebbero essere associate all’intero circuito
possono essere attribuite a singoli componenti
● All’interno di un induttore i valori di B sono molto maggiori rispetto a
quelli assunti all’esterno
Il flusso di B concatenato con il circuito è praticamente determinato
dai soli contributi dei flussi negli induttori
● All’interno di un condensatore i valori di D sono molto maggiori rispetto
a quelli assunti all’esterno
La densità di carica sulla superficie del conduttore assume valori
significativi solo sulle armature dei condensatori
6
Esempio
c 0
Induttore
Resistori
Β0
D0
c 0
D0
Β0
Conduttore
ideale
Condensatore
Generatore
7
Induttori e condensatori in regime stazionario
● Se il conduttore può essere considerato ideale, la tensione
dell’induttore è nulla
In regime stazionario un induttore equivale a un cortocircuito
● Dato che le armature del condensatore sono separate da un
dielettrico, la corrente nel condensatore è nulla
In regime stazionario un condensatore equivale a un circuito
aperto
In regime stazionario è possibile determinare le correnti degli
induttori e le tensioni dei condensatori studiando circuiti formati
solo da componenti resistivi
Per gli induttori, dai valori delle correnti si possono ricavare i
flussi di induzione magnetica
Per i condensatori, dai valori delle tensioni si possono
ricavare le cariche
8
Esempio
Q
Q
LiL
Q CvC
iL
VG
R1 R2
vC VG
R2
R1 R2
9
Elettromagnetismo non stazionario
● Equazioni fondamentali
Β
E
D c
t
D
H
J
B 0
t
J c
t
● Equazioni di legame materiale per un mezzo lineare isotropo
D E
B H
J E Ei
10
Elettromagnetismo non stazionario
● Il campo elettrico E non è conservativo
L’integrale di linea del campo elettrico (tensione) tra due punti A e
B dipende dal percorso
Non può essere espresso come differenza di potenziale
TAB ()
E tˆ dl
AB
● La densità di corrente J non è solenoidale
● E’ solenoidale la densità di corrente totale JT costituita dalla somma
delle densità di corrente di conduzione e di spostamento
D c
D
t
c
t
JT J
J
D
J
JT 0
t
11
Elettromagnetismo non stazionario
● E non è conservativo
Non si può definire in modo univoco la tensione tra due terminali
Non vale la legge di Kirchhoff per le tensioni
● J non è solenoidale
La corrente attraverso la sezione trasversale di un tubo di flusso di J
in generale non è costante
Non vale la legge di Kirchhoff per le correnti
● Le interazioni tra i componenti di un sistema elettromagnetico non
possono essere descritte in termini di tensioni e correnti
● In particolare, non è possibile esprimere la potenza assorbita o erogata
da un componente mediante le tensioni e le correnti ai terminali
In condizioni non stazionarie il modello circuitale non è valido
12
Elettromagnetismo quasi stazionario
● Se le variazioni temporali delle grandezze elettromagnetiche
sono sufficientemente lente è possibile che, in determinate
regioni dello spazio, alcune delle derivate rispetto al tempo che
compaiono nelle equazioni fondamentali risultino trascurabili
● Quando si verifica questa situazione è possibile descrivere, in
via approssimata, l’evoluzione nel tempo di un sistema elettromagnetico facendo uso, istante per istante, di risultati che a
rigore valgono solo in condizioni stazionarie
In questo casi si dice che il sistema in oggetto è in condizioni
quasi stazionarie
13
Elettromagnetismo quasi stazionario
● Un sistema elettromagnetico in condizioni quasi stazionarie viene
descritto mediante equazioni ottenute trascurando alcune delle
derivate rispetto al tempo nelle equazioni fondamentali
● Per definire in cosa consiste l’approssimazione quasi stazionaria
è necessario specificare
che cosa si intende per variazioni “sufficientemente lente”
indicare in quali casi le derivate rispetto al tempo possono
essere considerate nulle e in quali non possono essere
trascurate
● Per ottenere indicazioni riguardo ai punti precedenti, può essere
utile confrontare i potenziali elettrico e magnetico dovuti a distribuzioni volumetriche di cariche e di correnti nel caso stazionario
e nel caso non stazionario
14
Potenziali elettromagnetici
● B è solenoidale può essere espresso come rotore di un
potenziale vettore A
B 0
B A
● Dalla legge di Faraday si ottiene
E
B
t
E
( A)
t
A
E
0
t
Si può esprimere il vettore E A t come gradiente di un
potenziale scalare V
E
A
V
t
15
Campo elettrico non stazionario
● Il campo elettrico non stazionario può essere espresso come
somma di un componente conservativo e uno non conservativo
E V
A
E c E nc
t
Valutando l’integrale di E su una linea chiusa si ottiene
ˆdl V tˆdl d A tˆdl
E
t
dt
d
0
Β nˆ dS
dt S
16
Determinazione dei potenziali
● In un mezzo lineare isotropo omogeneo la legge di Ampere-Maxwell
può essere posta nella forma
B J
E
t
● Si inseriscono le espressioni di B e di E in funzione dei potenziali A e V
A J
A
V
t
t
2A
V
2
A ( A) J
t
t
2
2A
V
A 2 ( A
) J
t
t
2
17
Determinazione dei potenziali
● Per definire in modo univoco il potenziale vettore si deve assegnare il
valore della sua divergenza
● In questo caso conviene imporre la condizione
A
V
t
Scelta di Lorentz
● In questo modo si ha
V
2A
A 2 ( A
) J
t
t
0
2
2A
A 2 J
t
2
Il potenziale vettore magnetico soddisfa un’equazione delle onde non
omogenea
18
Determinazione dei potenziali
● In un mezzo lineare isotropo omogeneo la legge di Gauss può essere
posta nella forma
E
c
● Si inserisce nell’equazione l’espressione di E in funzione dei potenziali
A e V, quindi, tenendo conto della scelta di Lorentz, si ottiene
A c
V
t
A
c
t
2 V
V 2 c
t
2 V
V
A
t
2
Anche il potenziale scalare elettrico soddisfa un’equazione delle onde
non omogenea
19
Determinazione dei potenziali
● Si può dimostrare che le soluzioni delle equazioni delle onde sono
2A
A 2 J
t
2 V
2
V 2 c
t
2
A(P, t )
J (Q, t rPQ / c)
d
rPQ
4
V(P, t )
1 c (Q, t rPQ / c)
d
rPQ
4
● La costante c rappresenta la velocità della luce nel mezzo in cui ha
sede il campo elettromagnetico
c
1
● In particolare nel vuoto si ha
c0
1
299792458 m/s
00
20
Potenziali ritardati
A(P, t )
J (Q, t rPQ / c)
d
rPQ
4
V(P, t )
1 c (Q, t rPQ / c)
d
rPQ
4
● A e V sono costituiti dalla somma di infiniti contributi ciascuno dei quali
rappresenta un’onda sferica generata in un punto Q che si propaga con
velocità c
Il campo elettrico e il campo magnetico nel punto P all’istante t non
sono determinati dai valori all’istante t di J e c
L’effetto dovuto ad una densità di corrente o di carica in un punto Q
viene avvertito nel punto P con un ritardo proporzionale alla distanza
tra i punti considerati
21
Confronto con il caso stazionario
Condizioni stazionarie
Condizioni non stazionarie
A J
2 V c
2A
A 2 J
t
2 V
2
V 2 c
t
2
2
A(P)
J (Q)
d
4 rPQ
A(P, t )
J (Q, t rPQ / c)
d
4
rPQ
V(P)
1 c (Q)
d
4 rPQ
V(P, t )
1 c (Q, t rPQ / c)
d
4
rPQ
22
Confronto con il caso stazionario
● In condizioni stazionarie non si hanno effetti di propagazione
● Il campo elettromagnetico all’istante t si può identificare con il
campo stazionario prodotto da distribuzioni di cariche e correnti
con densità costanti e uguali a quelle relative all’istante t se è
possibile trascurare i ritardi di propagazione
A(P, t )
J (Q, t )
d
4 rPQ
V(P, t )
1 c (Q, t )
d
4 rPQ
E’ necessario che in un intervallo di tempo pari al massimo ritardo
di propagazione che si può avere all’interno del sistema le grandezze elettromagnetiche siano praticamente costanti
23
Confronto con il caso stazionario
● Si considera il caso in cui le grandezze elettromagnetiche variano nel
tempo con legge sinusoidale e quindi si ha
c (Q, t ) M (Q) cost (Q)
J (Q, t ) J M (Q) cost J (Q)
2
2f
T
pulsazione
f frequenza
T periodo
● Variazioni di tipo più generale possono essere espresse mediante
sovrapposizione di funzioni sinusoidali (serie o integrali di Fourier)
Le considerazioni relative al caso sinusoidale possono essere estese a
situazioni più generali riferendole alla massima frequenza che occorre
considerare
24
Confronto con il caso stazionario
● Se c varia con legge sinusoidale si ha
rPQ
(Q)
) M (Q) cos t
c
c
rPQ
r
M (Q) sent (Q)sen PQ
M (Q) cost (Q)cos
c
c
t
t
M (Q) cost (Q)cos 2 D M (Q) sent (Q)sen 2 D
T
T
C (Q, t
rPQ
● T indica il periodo e tD il tempo di ritardo dal punto Q al punto P
rPQ
2
t
T
D
c
● Un’espressione analoga vale per J
25
Approssimazione quasi stazionaria
● Se in tutti i punti del sistema vale la condizione
T t D
risulta
rPQ
c
t
cos 2 D 1
T
t
sen 2 D 0
T
P Q
c (Q, t
J (Q, t
rPQ
c
rPQ
c
) M (Q) cost (Q) c (Q, t )
) J M (Q) cost J (Q) J (Q, t )
Quindi si ha
A(P, t )
J (Q, t )
d
4 rPQ
V(P, t )
1 c (Q, t )
d
4 rPQ
In ogni istante t il campo elettromagnetico
coincide con il campo stazionario generato
da distribuzioni di carica e di corrente costanti con densità J(Q,t) e c(Q,t)
26
Limiti di validità dell’approssimazione quasi stazionaria
● Se la massima distanza tra due punti del sistema è dmax, il massimo
ritardo di propagazione è
t D max
d max
c
L’approssimazione quasi stazionaria è valida se, alla massima frequenza che interessa considerare, il periodo della variazione delle grandezze elettromagnetiche è molto grande rispetto al massimo ritardo di propagazione
T t D max
● La condizione può essere posta nella forma
d max cT
c
f
lunghezza d’onda
La massima dimensione del sistema deve essere molto piccola rispetto
alla lunghezza d’onda corrispondente alla massima frequenza che
interessa considerare
27
Limiti di validità dell’approssimazione quasi stazionaria
f
T
c0
50 Hz
20 ms
6000 km
100 Hz
10 ms
3000 km
1 kHz
1 ms
300 km
10 kHz
100 s
30 km
20 kHz
50 s
15 km
100 kHz
10 s
3 km
1 MHz
1 s
300 m
10 MHz
100 ns
30 m
100 MHz
10 ns
3m
1 GHz
1 ns
300 mm
10 GHz
100 ps
30 mm
28
Approssimazione quasi stazionaria
● In condizioni quasi stazionarie si approssimano i potenziali con le
soluzioni delle equazioni
2 A(t ) J (t )
2 V(t )
c (t )
Le derivate seconde rispetto a t dei potenziali devono essere trascurabili
2A
0
t 2
2 V
0
t 2
● La presenza di queste derivate dipende dalla presenza simultanea delle
derivate temporali di B e D nelle equazioni di Maxwell
Se si annulla almeno una di queste derivate si annullano le derivate
seconde
Le derivate seconde sono trascurabili se in ogni punto del sistema è
verificata almeno una delle condizioni
D
0 oppure
t
B
0
t
29
Approssimazione quasi stazionaria
● Si considera il caso in cui B e D sono funzioni sinusoidali del tempo
B(P, t ) B M (P) cost B (P)
D(P, t ) D M (P) cost D (P)
● In questo caso le loro derivate sono funzioni sinusoidali del tempo con
ampiezza proporzionale all’ampiezza di B e D
B
B M (P) sent B (P) B M (P) cos t B (P)
t
2
D
D M (P) sent D (P) D M (P) cos t D (P)
t
2
In queste condizioni si può assumere che le derivate siano trascurabili
nelle regioni in cui B e D sono trascurabili
30
Esempio
C
0
t
Induttore
Β
0
t
D
0
t
Resistori
C
0
t
Β
0
t
Conduttore
ideale
D
0
t
Condensatore
Generatore
31
Circuiti in condizioni quasi stazionarie
● Se la frequenza è sufficientemente bassa, si può assumere che sia
Β
0
t
negli induttori
Β
0 nelle rimanenti regioni
t
D
0
t
nei condensatori
D
0 nelle rimanenti regioni
t
● In queste condizioni il sistema può essere ancora descritto mediante
un modello circuitale a condizione che le superfici limite dei componenti
siano definite in modo che derivate di B e di D possano essere diverse
da zero solo al loro interno
(Ad esempio, non si può racchiudere in una superficie limite una sola
armatura di un condensatore)
● In questo modo, anche le derivate dei flussi di B e di D attraverso le
superfici limite sono nulle
32
Circuiti in condizioni quasi stazionarie
● In condizioni non stazionarie è solenoidale la densità di corrente
totale JT
D
JT J
0
t
● Nelle regioni in cui la derivata di D è trascurabile (e in particolare
all’esterno delle superfici limite dei componenti) si ha
J 0
Quindi, dall’equazione di continuità si ricava che in queste regioni
vale anche la condizione
C
0
t
33
Circuiti in condizioni quasi stazionarie
Regione esterna:
Componenti:
All’interno delle superfici limite, in ogni punto
è verificata almeno una delle condizioni
D
Β
0 e
0
t
t
Β
D
0 oppure
0
t
t
34
Circuiti in condizioni quasi stazionarie
● Nella regione esterna e sulle superfici limite E è conservativo e J
è solenoidale
Si possono definire in modo univoco le tensioni e le correnti ai
terminali dei componenti
Valgono le leggi di Kirchhoff (se si considerano linee chiuse e
superfici chiuse interamente contenute nella regione esterna)
● Come in regime stazionario, si può esprimere il flusso del vettore
di Poynting attraverso la superficie limite di un componente nella
forma
E H nˆ dS V J nˆ dS
S
S
Sono ancora valide le espressioni delle potenze scambiate dai
componenti in funzione delle tensioni e delle correnti che sono
state ricavate nel caso stazionario
35
Induttore
● Ipotesi:
Avvolgimento costituito da un conduttore filiforme con sezione s
e conducibilità
La derivata di B rispetto a t assume valori apprezzabilmente diversi
da zero solo all’interno della superficie chiusa S
La derivata di D rispetto a t può essere considerata ovunque nulla
S
Superficie limite
A
B
Β
0
t
D
0
t
Β
0
t
36
Induttore
● J è ovunque solenoidale la corrente ha lo stesso valore i Js in
ogni sezione del conduttore
● All’esterno di S E è irrotazionale la tensione tra i terminali A e B
dell’induttore può essere valutata integrando il campo elettrico lungo
una linea arbitraria 0 esterna alla superficie S
B
v AB
E tˆ dl
A 0
S
Superficie limite
A i
0
Β
0
t
B
D
0
t
Β
0
t
37
Induttore
● Applicando la legge di Ohm al conduttore si ha
B
B
B
J s
dl
E
t̂
dl
dl
i
A
A s
A s Ri
● Si sottrae e si somma a primo membro l’integrale di E su 0
B
B
B
A
A 0
A 0
E tˆ dl E tˆ dl E tˆ dl Ri
● I primi due termini della rappresentano
la circuitazione di E sulla linea chiusa
formata da e 0
S
A i
0
B
B
E tˆ dl E tˆ dl Ri
0
A 0
38
Induttore
● Per la legge di Faraday
E t̂ dl
0
d
dt
flusso di B concatenato con la linea 0
● All’esterno di S la derivata di B rispetto a t è trascurabile il valore
dell’integrale non dipende dalla particolare linea 0 considerata
Quindi si ottiene
d
v AB Ri
dt
v AB
S
di
Ri L
dt
dove
A i
0
L
i
rappresenta l’induttanza dell’avvolgimento
B
39
Induttore ideale
● Se la resistenza dell’avvolgimento, R, è trascurabile è possibile
rappresentare il componente con un induttore ideale
(t ) Li (t )
d
v(t )
dt
Equazione
caratteristica
di
v(t ) L
dt
Simbolo
(v e i orientate secondo la convenzione dell’utilizzatore)
● Se la resistenza non è trascurabile si può rappresentare
il componente mediante un bipolo equivalente formato
da un induttore ideale e un resistore collegati in serie
v Ri L
di
dt
40
Induttore ideale
● Integrando l’equazione caratteristica a partire da un istante iniziale t0
si può esprimere la corrente in funzione della tensione
di ()
v
(
)
d
L
t
t d d
0
0
t
t
t
1
i
(
t
)
i
(
t
)
v()d
0
L t0
● In generale si può assumere che valga la condizione
lim i (t ) 0
t
(in pratica esiste sempre un istante iniziale prima del quale la corrente
e la tensione sono identicamente nulle)
L’espressione della corrente può essere posta nella forma
t
1
i (t ) v()d
L
la corrente all’istante t dipende dall’andamento
della tensione in tutti gli istanti precedenti
41
Induttore – Proprietà di memoria
● Corrente all’istante t t0
t
1 0
I 0 i(t0 ) v()d
L
● Flusso all’istante t t0
0 (t0 ) LI 0
● Corrente per t t0
1
1 0
1
i(t ) v()d v()d v()d
L
L
L t0
t
t
1
1
I 0 v()d 0 v()d
L t0
L L t0
t
t
t
Per determinare la corrente per t t0 occorre conoscere
la corrente (o il flusso) per t t0
l’andamento della tensione per t t0
Il valore della corrente (o del flusso) all’istante t0 riassume il
comportamento del componente per t t0
42
Condensatore
● Ipotesi:
La derivata di D rispetto a t assume valori apprezzabilmente diversi
da zero solo all’interno della superficie chiusa S
La densità di carica assume valori apprezzabilmente diversi da zero
solo sulle armature del condensatore
La derivata di B rispetto a t può essere considerata ovunque nulla
A
iA
Superficie limite
S
n̂
Β
0
t
D
0
t
B
D
0
t
iB
43
Condensatore
● La corrente di spostamento attraverso la superficie S è nulla
Su S J è solenoidale
La corrente iA è uguale in ogni istante alla corrente iB
J n̂ dS i
A
iB 0
i A iB i
S
● Il campo elettrico è identico, in ogni istante, ad un campo stazionario
Vale la relazione
Q
A
B
ˆ dl v AB (t ) Q(t )
E
t
C
A
iA
n̂
n̂ A
● Dall’equazione di continuità, considerando la superficie SA, si ottiene
dQ
i J nˆ A dS
dt
SA
SA
S
Q
B
iB
44
Condensatore
● Combinando le due ultime equazioni si ottiene la relazione costitutiva
del condensatore
Equazione
Q(t ) Cv(t )
caratteristica
Simbolo
i (t )
dQ
dt
i (t ) C
dv
dt
(v e i orientate secondo la convenzione dell’utilizzatore)
● Integrando rispetto al tempo si può esprimere la tensione in funzione
della corrente
t
1
v(t ) v(t0 ) i ()d
C t0
oppure, assumendo lim v(t ) 0
t
v(t )
1
i ()d
C
t
la tensione all’istante t dipende dall’andamento
della corrente in tutti gli istanti precedenti
45
Condensatore – Proprietà di memoria
t
● Tensione all’istante t t0
1 0
V0 v(t0 ) i( )d
C
● Carica all’istante t t0
Q0 Q(t0 ) CV0
● Tensione per t t0
1
1 0
1
v(t ) i( )d i( )d i()d
C
C
C t0
t
t
Q
1
1
V0 i( )d 0 i( )d
C t0
C C t0
t
t
t
Per determinare la tensione per t t0 occorre conoscere
la tensione (o la carica) per t t0
l’andamento della corrente per t t0
Il valore della tensione (o della carica) all’istante t0 riassume il
comportamento del componente per t t0
46
Corrente di spostamento
● Si considerano due superfici aventi per contorno la linea
S1 esterna al condensatore
S2 passante tra le armature del condensatore
● La densità di corrente totale è solenoidale
D
J
nˆ dS 0
dt
S1 S 2
● La corrente di spostamento attraverso
S1 è nulla
● La corrente di conduzione attraverso
S2 è nulla
J nˆ 1dS
S1
n̂1
n̂ 2
i
i
t̂
D
S dt nˆ 2 dS
2
S1 S2
D
t
47
Corrente di spostamento
● La circuitazione del campo magnetico sulla è uguale alla corrente
totale concatenata con la linea
● In condizioni quasi stazionarie le linee di campo di H non sono
concatenate con i tubi di flusso di J, ma con quelli di JT
● Il flusso di JT attraverso S1 è dovuto
alla sola corrente di conduzione
● Il flusso di JT attraverso S2 è dovuto
alla sola corrente di spostamento
ˆdl J nˆ 1dS D nˆ 2 dS
H
t
t
S1
S2
i
n̂1
n̂ 2
i
i
t̂
S1 S2
D
t
48
Componenti resistivi e componenti dinamici
● Componenti privi di memoria (resistivi)
Le equazioni caratteristiche sono algebriche
Le equazioni mettono in relazione valori delle correnti e delle
tensioni allo stesso istante
I componenti introdotti nello studio dell’elettrodinamica stazionaria
rientrano tutti in questa categoria
● Componenti dotati di memoria (dinamici)
Le equazioni caratteristiche sono differenziali
Le equazioni coinvolgono valori delle tensioni e delle correnti relativi
a istanti diversi
Induttori e condensatori rientrano in questa categoria
49
Circuiti resistivi e circuiti dinamici
● Circuiti resistivi: circuiti formati esclusivamente da componenti resistivi
le equazioni del circuito costituiscono un sistema di equazioni
algebriche
i valori delle tensioni e delle correnti (risposte) in un certo istante
dipendono solo dai valori delle grandezze impresse dei generatori
indipendenti (ingressi) allo stesso istante
● Circuiti dinamici: circuiti che contengono almeno un componente
dinamico (induttore o condensatore)
le equazioni del circuito costituiscono un sistema di equazioni
differenziali
i valori delle risposte a un certo istante dipendono anche dagli
andamenti degli ingressi negli istanti precedenti
50
Definizioni
● Energia assorbita da un componente nell’intervallo [t1 t2]
t2
w a (t1 , t 2 ) p a (t )dt
pa potenza assorbita
t1
● Energia assorbita da un componente fino all’istante t
t
w a (t ) p a ()d
● Energia erogata da un componente nell’intervallo [t1 t2]
t2
w e (t1 , t 2 ) p e (t )dt w a (t1 , t 2 )
pe potenza erogata
t1
● Energia erogata da un componente fino all’istante t
t
w e (t ) p e ()d w a (t )
51
Componenti attivi e passivi
● Per classificare come attivi o passivi i componenti dinamici
occorre generalizzare la definizione introdotta per i componenti
resistivi
● Componente passivo:
per tutti i possibili andamenti delle tensioni e delle correnti
descrittive compatibili con le relazioni costitutive risulta
wa(t) ≥ 0
t
● Componente attivo:
esistono andamenti delle tensioni e delle correnti descrittive
compatibili con le relazioni costitutive tali che, per alcuni valori
di t, risulta
wa(t) < 0
Un componente attivo è un componente in grado di generare
energia elettrica
52
Componenti passivi
● Energia assorbita fino all’istante t2
t2
t1
t2
t1
w a (t 2 ) p a (t )dt p a (t )dt p a (t )dt w a (t1 ) w a (t1 , t 2 )
● Per un componente passivo deve essere
w a (t 2 ) 0 w a (t1 ) w a (t1 , t 2 ) 0 w a (t1 ) w e (t1 , t 2 )
we(t1,t2) può essere positiva il componente può erogare
energia nell’intervallo [t1 t2]
per un componente passivo l’energia erogata in un intervallo
[t1 t2] non può superare l’energia assorbita fino all’istante
iniziale dell’intervallo
53
Componenti passivi
● Un componente passivo può accumulare (almeno in parte)
l’energia assorbita e, in seguito, restituire l’energia accumulata
un comportamento di questo tipo implica un vincolo i valori
delle tensioni e correnti nell’intervallo [t1 t2] da cui dipende
we(t1,t2) e i valori nell’intervallo [∞ t1] da cui dipende wa(t1)
il componente deve essere dotato di memoria
per un componente privo di memoria deve essere verificata la
condizione
wa(t1,t2) ≥ 0
t1, t2
questo richiede che sia anche pa 0 in ogni istante e per
ogni condizione di funzionamento, coerentemente con la
definizione di componente passivo introdotta nello studio
dell’elettrodinamica stazionaria
54
Induttore – Comportamento energetico
● Potenza assorbita:
d i d 1 2
L i (t )
dt dt 2
● Energia assorbita fino all’istante t
p a (t ) v(t ) i(t ) L i(t )
1 2
1 2 (t )
d 1 2
w a (t ) p a ()d L i () d L i (t )
2
2 L
d 2
t
t
L’energia assorbita fino all’istante t è determinata se è noto il
valore all’istante t della corrente o del flusso
Se L > 0 l’energia assorbita fino all’istante t è ≥ 0 t
Se L > 0 l’induttore è un componente passivo
55
Induttore – Comportamento energetico
● Energia assorbita nell’intervallo [t1 t2]
t2
1 2
1
L i (t 2 ) i 2 (t1 )
2 (t 2 ) 2 (t1 )
2
2L
t1
Non dipende dall’andamento di v(t) e i(t) nell’intervallo [t1 t2]
Dipende solo dai valori di i (o di ) agli istanti t1 e t2
E’ nulla se i(t1) i(t2) (e quindi (t1) (t2))
w a (t1 , t 2 ) p a (t )dt
● Per un induttore passivo (L > 0)
L’energia assorbita nell’intervallo [t1 t2] è negativa se |i(t2)| < |i(t1)|
L’energia erogata nell’intervallo [t1 t2] non può superare l’energia
assorbita fino a t1
w e (t1 , t 2 ) w a (t1 , t 2 )
1 2
1
L i (t1 ) i 2 (t 2 ) L i 2 (t1 ) w a (t1 )
2
2
L’induttore accumula l’energia assorbita ed è in grado di restituirla
integralmente
56
Condensatore – Comportamento energetico
● Potenza assorbita:
d v d 1
C v 2 (t )
dt dt 2
● Energia assorbita fino all’istante t
p a (t ) v(t ) i(t ) C v(t )
1
1 Q 2 (t )
d 1
2
2
w a (t ) p a ()d C v () d C v (t )
2
2 C
d 2
t
t
L’energia assorbita fino all’istante t è determinata se è noto il
valore all’istante t della tensione o della carica
Se C > 0 l’energia assorbita fino all’istante t è 0 t
Se C > 0 il condensatore è un componente passivo
57
Condensatore – Comportamento energetico
● Energia assorbita nell’intervallo [t1 t2]
t2
1
1
w a (t1 , t 2 ) p a (t )dt C v 2 (t 2 ) v 2 (t1 )
Q 2 (t 2 ) Q 2 (t1 )
2
2C
t1
Non dipende dall’andamento di i(t) e v(t) nell’intervallo [t1 t2]
Dipende solo dai valori di v (o di Q) agli istanti t1 e t2
E’ nulla se v(t1) v(t2) (e quindi Q(t1) Q(t2))
● Per un condensatore passivo (C > 0)
L’energia assorbita nell’intervallo [t1 t2] è negativa se |v(t2)| < |v(t1)|
L’energia erogata nell’intervallo [t1 t2] non può superare l’energia
assorbita fino a t1
1
1
w e (t1 , t 2 ) w a (t1 , t 2 ) C v 2 (t1 ) v 2 (t 2 ) C v 2 (t1 ) w a (t1 )
2
2
Il condensatore accumula l’energia assorbita ed è in grado di
restituirla integralmente
58
Induttore – Proprietà di continuità
● In un induttore, se la tensione v(t) è limitata, la corrente i(t) è una
funzione continua del tempo
● Dimostrazione: Dato che
t
1
i(t ) v()d
L
la proprietà deriva direttamente dalla proprietà di continuità della
funzione integrale:
v(t) limitata M 0 : v(t ) M t
t e t risulta
t t
t t
t t
1
1
1
1
i(t t ) i(t ) v()d v() d Md Mt
L t
L t
L t
L
di conseguenza
lim i(t t ) i(t ) 0
t 0
quindi i(t) è continua
59
Condensatore – Proprietà di continuità
● In un condensatore, se la corrente i(t) è limitata, la tensione v(t)
è una funzione continua del tempo
● Dimostrazione: Dato che
t
1
v(t ) i()d
C
la proprietà deriva direttamente dalla proprietà di continuità della
funzione integrale
60
Induttori in serie
N
LKV v v k
k 1
i ik
LKI
( k 1,, N )
di
Relazioni
v k Lk k
costitutive
dt
( k 1,, N )
d ik N
di
di
Lk
LS
v Lk
dt k 1 dt
dt
k 1
N
N induttori in serie equivalgono a un induttore con induttanza
N
LS Lk
k 1
61
Induttori in parallelo
N
LKI
i ik
k 1
LKV v v k
( k 1,, N )
Relazioni i 1
k
costitutive
Lk
1
i
k 1 Lk
N
t
v
k
( )d ( k 1,, N )
N 1
v k ( )d
k 1 Lk
t
t
1
v( )d
LP
t
v()d
N induttori in parallelo equivalgono a un induttore con induttanza
LP
1
1
k 1 Lk
N
62
Condensatori in serie
N
LKV v v k
k 1
LKI
i ik
( k 1,, N )
Relazioni v 1
k
costitutive
Ck
1
v
k 1 Ck
N
t
i ()d
k
N 1
ik ( )d
k 1 Ck
t
( k 1,, N )
i
t
1
i( )d
CS
t
i()d
N condensatori in serie equivalgono a un condensatore con
capacità
1
CS N
1
k 1 Ck
63
Condensatori in parallelo
N
LKI i i k
k 1
LKV v v k
( k 1,, N )
Relazioni i C d v k
k
k
costitutive
dt
( k 1,, N )
d vk N
dv
dv
Ck
CP
i Ck
dt
dt
k 1
k 1 dt
N
N condensatori in parallelo equivalgono a un condensatore con
capacità
N
C P Ck
k 1
64