Prova scritta del 11 Settembre 2012
ESERCIZIO 1
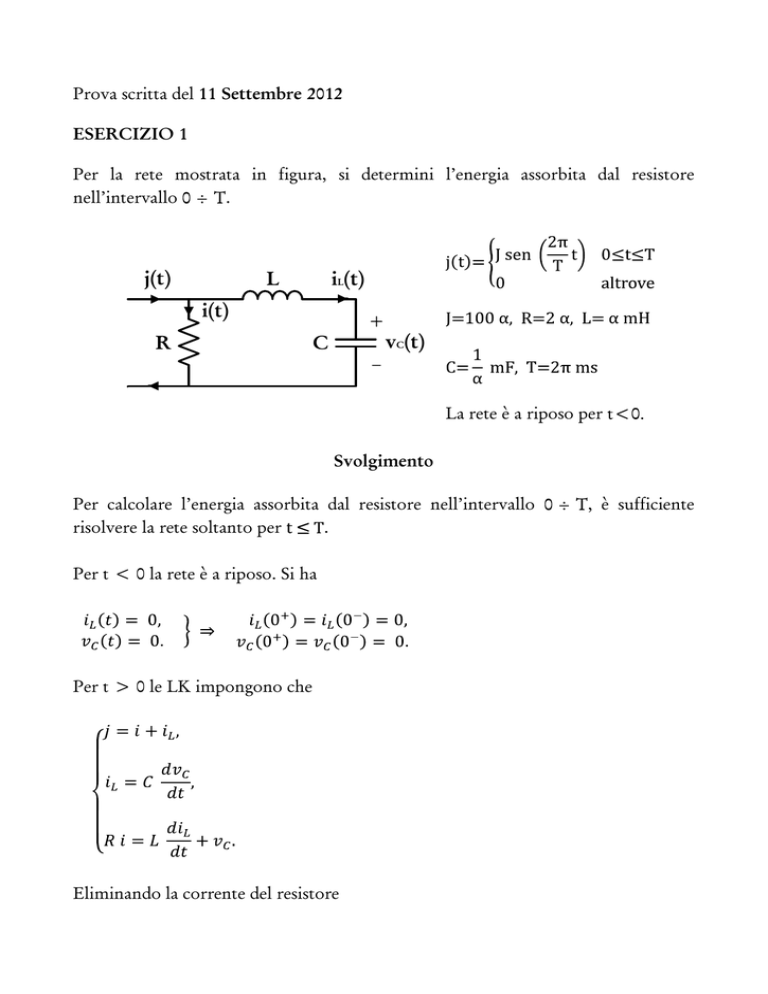
Per la rete mostrata in figura, si determini l’energia assorbita dal resistore
.
nell’intervallo
j(t)
iL(t)
L
i(t)
R
+
vC(t)
C
–
La rete è a riposo per
Svolgimento
Per calcolare l’energia assorbita dal resistore nell’intervallo
.
risolvere la rete soltanto per
Per t < 0 la rete è a riposo. Si ha
Per t > 0 le LK impongono che
Eliminando la corrente del resistore
, è sufficiente
il precedente sistema si riduce alle due equazioni che seguono
Per determinare le condizioni iniziali, occorre passare al limite per t
adoperare le condizioni di raccordo
0+ ed
In tal modo, si ha
Inoltre, derivando la prima equazione del sistema si ottiene l’espressione della
derivata di . Sostituendo quest’ultima nella seconda equazione, ed aggiungendo le
condizioni iniziali, si ottenere il seguente problema di Cauchy per la corrente
circolante nell’induttore
Il polinomio caratteristico dell’omogenea associata è
Le cui radici, essendo nullo il discriminante dell’equazione caratteristica
sono reali e coincidenti:
L’integrale generale dell’omogenea associata assume la forma
L’integrale particolare dell’equazione completa può essere trovato risolvendo la
rete nel dominio dei fasori. Osservando che, a regime, l’induttore e il condensatore
sono in risonanza serie, si ricava subito che
L’integrale generale dell’equazione completa è, quindi
Forzando le condizioni iniziali, si ottiene
Per
dunque, si ha
L’energia assorbita dal resistore nell’intervallo di tempo
Osservando che
si ottiene come
, si può scrivere
ESERCIZIO 2
Per la rete trifase mostrata in figura, scegliere il tipo di rifasamento (terna di
condensatori collegati a stella o a triangolo), motivando la scelta e rifasare a
1
2
3
R
XL
R
XL
R
XL
La terna di alimentazione è
simmetrica.
Svolgimento
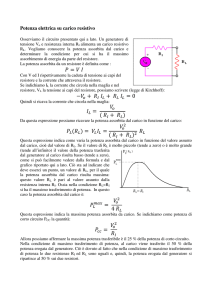
Ricordando che, a parità di potenza reattiva assorbita, il costo di un condensatore
cresce al diminuire della caduta di tensione ai suoi capi e al crescere della capacità,
conviene rifasare collegando i condensatori a triangolo, come mostrato nella figura
seguente
1
2
3
C
R
XL
R
XL
R
XL
C
C
Prima dell’inserimento della batteria di condensatori, l’angolo di fase del carico
equilibrato è pari a
e si può scrivere che
.
Dopo l’inserimento della batteria di condensatori, si ha
Poiché si vuole rifasare completamente il carico, bisogna imporre
Quindi, si può scrivere
, cioè
.
Poiché
il valore della capacità da utilizzare per rifasare il circuito si ottiene da
dove V rappresenta il modulo della tensione che cade ai capi di ciascun
condensatore, che nel nostro caso è pari al modulo delle tensioni concatenate
Il valore di P si ottiene ricordando che, nel caso di carico equilibrato, si ha
in cui I è il modulo delle correnti di linea.
Poiché
si ha
Quindi
Noto il valore di I, possiamo calcolare la potenza attiva P
Infine, possiamo calcolare il valore della capacità che consente di rifasare
completamente il carico: