VARIABILI CASUALI
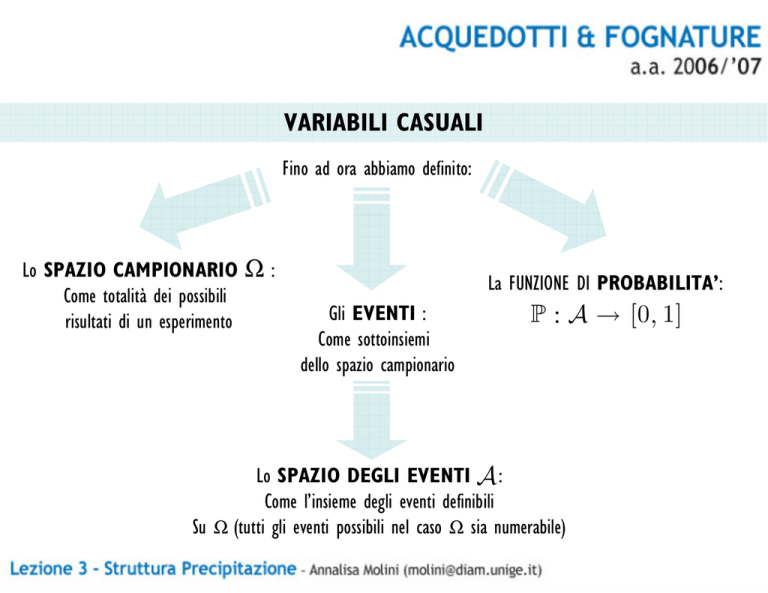
Fino ad ora abbiamo definito:
Lo SPAZIO CAMPIONARIO
Come totalità dei possibili
risultati di un esperimento
Ω:
La FUNZIONE DI PROBABILITA’:
Gli EVENTI :
Come sottoinsiemi
dello spazio campionario
P : A → [0, 1]
Lo SPAZIO DEGLI EVENTI A :
Come l’insieme degli eventi definibili
Su Ω (tutti gli eventi possibili nel caso Ω sia numerabile)
VARIABILI CASUALI
Quindi abbiamo introdotto il concetto di
SPAZIO DI PROBABILITA’ dato dalla terna:
(Ω, A, P)
Presentiamo ora le nozioni di:
VARIABILE ALEATORIA:
“descrive” gli eventi ed ha come dominio
di definizione lo spazio campionario
FUNZIONE DI DISTRIBUZIONE
CUMULATA:
Definisce la probabilità degli eventi in
termini di variabili casuali
COS’E’ UNA VARIABILE CASUALE?
Dato un esperimento, una Variabile Casuale (o Variabile Aleatoria)
è una funzione che fa corrispondere un numero reale
a ogni esito dell’esperimento
In generale è una
variabile il cui valore sia:
AFFETTO DA
FORTE INCERTEZZA
COMUNQUE “NON
DETERMINISTICAMENTE”
DEFINIBILE
IMPREDICIBILE
COS’E’ UNA VARIABILE CASUALE?
Dato quindi uno
SPAZIO DI PROBABILITA’
(Ω, A, P)
Una Variabile Casuale (o Variabile Aleatoria) X
è una funzione avente come dominio Ω e codominio la retta reale (o un suo sottoinsieme):
X:Ω→R
Esiste cioè un valore numerico della X associato ad ogno realizzazione dell’esperimento
FUNZIONE DI DISTRIBUZIONE CUMULATA
(IN GENERALE)
Si definisce FUNZIONE DI DISTRIBUZIONE CUMULATA o FUNZIONE DI RIPARTIZIONE
di una variabile casuale X, e si indica con FX quell’applicazione:
FX : R → [0, 1]
Tale che:
FX(x) = P [X x] = P [ω : X(ω) x]
∀ x∈R
FUNZIONE DI DISTRIBUZIONE CUMULATA
(IN GENERALE)
Alcune proprietà della FUNZIONE DI DISTRIBUZIONE CUMULATA
o FUNZIONE DI RIPARTIZIONE:
1
lim FX(x) = 0 e
x→∞
lim FX(x) = 1
x→+∞
2
FX(x) e monotona non decrescente (cioe per a < b, FX(a) FX(b))
3 FX(x) e continua da destra :
lim FX(x + h) = FX(x)
h→0+
con h > 0
VARIABILI ALEATORIE
Le Variabili Casuali si distinguono in:
Variabili Casuali
DISCRETE
Variabili Casuali
CONTINUE
VARIABILI ALEATORIE DISCRETE
Una variabile casuale si definisce discreta se i valori assunti da X sono una quantità numerabile, cioè esiste un
insieme finito o numerabile di numeri reali, diciamo x1,…,xn, tale che X
Assuma valori in questo insieme
FUNZIONI DI MASSA DI PROBABILITA’
Se X è una variabile aleatoria discreta, che assume valori distinti x1,…,xn, (che supponiamo per
semplicità ordinati in modo crescente) allora la FUNZIONE DI MASSA DI PROBABILITA’ o FUNZIONE DI
DENSITA’ DISCRETA di X, indicata con px è definita come:
pX =
P(X = x) se x = x 1, ..., x n
0 altrimenti
Pmf= probability mass
function
p X(x i) = P(X = x i)
i = 1, ..., n, ...
FUNZIONI DI MASSA DI PROBABILITA’
Si ha inoltre che:
0 p X(x) 1 ∀ x ∈ A
p X(x i) = 1
i
p X(x) = 0 ∀ x ∈ A
Inoltre, nota px si può facilmente ottenere Fx come segue:
FX(x) = P (X x) =
p X(x i)
x it.c. x ix
Ed analogamente:
p X(x i) = FX(x i) lim FX(x i h) = FX(x i) FX(x i1)
h →0
FUNZIONI DI MASSA DI PROBABILITA’
p X(x)
FX(x)
ALCUNE FAMIGLIE DI
VARIABILI ALEATORIE DISCRETE
DISTRIBUZIONE BINOMIALE
DISTRIBUZIONE DI POISSON
DISTRIBUZIONE GEOMETRICA
TEMPO DI RITORNO E DISTRIBUZIONE GEOMETRICA
Abbiamo visto come la legge di probabilità abbinata ad una V.A. geometrica sia data da:
(Dove p è compreso tra 0 ed 1) ed esprima la probabilità di ottenere un successo al k-esimo
Lancio (assimilabile al tempo di attesa discreto che si deve consumare prima di avere un successo)
Poniamo che la v.a. Yi rappresenti ad esempio, il valore del massimo picco di piena registrato nell’anno i.
Se gli Yi sono indipendenti, la probabilità che l’intervallo di tempo T* tra le due eccedenze di una piena
di intensità y (qui inteso come intervallo di tempo discreto=numero di anni) sia uguale a n è data da:
P(T = n) = P(Y 1 < y) P(Y 2 < y) ... P(Y n1 < y) P(Y n > y)
T Geometrica → E(T ) =
1
P(Y>y)
=T
VARIABILI ALEATORIE CONTINUE
Legge di probabilità per una variabile continua
Funzione di densità di probabilità (pdf):
Rappresenta il caso al limite di un poligono di frequenza relativa applicato ad un campione di numerosità
infinita e con la larghezza delle classi tendente a 0
f X(x)
f X(x) 0 ∀ x reale
P[x 1 X x 2] =
x2
x1
f X(x)dx
VARIABILI ALEATORIE CONTINUE
P(Ω) =
+∞
∞
f X(x)dx = 1
FX(x) = P[X x] =
dF X(x)
dx
x
(u)du
∞ f X
= f X(x)
ALCUNE FAMIGLIE DI
VARIABILI ALEATORIE CONTINUE
Distribuzione di Gauss
Distribuzione
Normale
Standard
ALCUNE FAMIGLIE DI
VARIABILI ALEATORIE CONTINUE
Distribuzione Lognormale
ALCUNE FAMIGLIE DI
VARIABILI ALEATORIE CONTINUE
Distribuzione esponenziale
ALCUNE FAMIGLIE DI
VARIABILI ALEATORIE CONTINUE
Distribuzione doppio-esponenziale
MEDIA E VARIANZA DI
UNA VARIABILE CASUALE DISCRETA
Se X è una V.A. discreta ed assume valori x1,…,xn, allora la media di X (E(X) o µ(x)) è data, come nel
caso delle V.C. empiriche da:
E(X) =
x ip X(x i)
i
Mentre la sua varianza è data da:
2(
! X) =
i
(x i E(X))2p X(x i) = E(X 2) [E(X)] 2
MEDIA E VARIANZA DI
UNA VARIABILE CASUALE CONTINUA
E(X) =
! 2(X) =
+∞
+∞
∞
xf X(x)dx
2
[
(
)
(
)]
x
x
dx
E
X
f
X
∞