Fisica Generale LA

Fisica Generale LA
Prof. Nicola Semprini Cesari
Prova Scritta del 10 Giugno 2015
Meccanica
Q1) Immaginando di collocare la massa m1 nella origine del riferimento, esprimere, nel sistema di
coordinate cartesiano, l’energia potenziale gravitazionale di una massa m2 posizionata nel generico punto
P(x,y,z) dello spazio. Dalla relazione F  V calcolare anche l’espressione della forza gravitazionale.
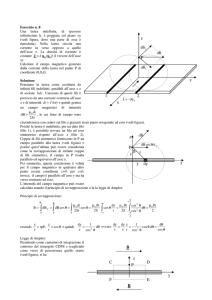
Q2) Un punto materiale di massa m si muove lungo una traiettoria
circolare a seguito della forza esercitata da due fili inestensibili di
lunghezza l1 ed l2 fissati all’altro estremo su di una asta verticale ad una
distanza h (vedi figura). Determinare la tensione T1 del filo orizzontale
in funzione della velocità angolare  del punto materiale. Discutere le
differenti situazioni possibili.
h
l2
l1
Q3) Data una lastra omogenea di lato L e densità superficiale di massa
 dimostrare che il suo centro di massa cade nel centro geometrico
della lastra stessa.
Q4) Una ruota omogenea di massa M e raggio R, libera di ruotare
attorno ad un asse orizzontale passante per il suo centro, è soggetta
alla azione di due funicelle inestensibili di massa trascurabile alle cui
estremità sono fissate due masse m1 ed m2 (m1>m2). Determinare
l’accelerazione verticale della massa m1.
Q5) Enunciare e dimostrare il teorema di Konig per l’energia cinetica di
un sistema rigido di punti materiali.
Q6) Spiegare cosa sono le forze inerziali, scrivere e commentare i
diversi termini che compaiono nella loro espressione.
m2
m1
Termodinamica
Q1) Commentare le trasformazioni del ciclo di Carnot e calcolarne il rendimento.
Q2) Calcolare la relazione esistente tra temperatura e volume nel caso di una trasformazione adiabatica
quasi statica.
Q3) Commentare il significato fisico del primo principio della termodinamica.
Soluzioni Meccanica
Q1)
m1m2
m1m2
 G
2
r
x  y2  z2
V  G
F  V  
m1m2
mm r
mm
V
V
V ˆ
ˆ
ıˆ 
k  G 2
( xıˆ  y ˆ  zkˆ)  G 1 22
 G 1 2 2 rˆ
2
2 3/2
x
y
z
(x  y  z )
|r | |r |
r
Q2)
F  ma
 T1ıˆr  T2 cos ıˆr  T2 sin  kˆ  mgk  m  2 r ıˆr
T2 sin   mg

2
T1  T2 cos   m  l1
sin   h / l cos   l / l
2
1
2

mgl2

T2  h

T1  mgl2 l1  m  2l1
h l2

g
T1  m(  2  )
h
se   g / h il filo orizzontale esercita una tensione sul punto materiale; se   g / h la tensione del
filo orizzontale si annulla e la forza centripeta necessaria per sostenere il moto è data interamente dal filo
obliquo; se   g / h il filo dovrebbe esercitare una forza radiale uscente sul punto materiale ma poiché
ciò non è possibile (il filo può solo tirare non spingere) non esiste moto con questa caratteristica.
Q3)
N
rCM 
 m j rj
j 1
N
m
j 1
j

 lastra
L L
 dx dy ( xıˆ  y ˆ)

lastra
 dx dy

L L
(    x dx dy )ıˆ  (    y dx dy ) ˆ
0 0
0 0
L L
   dx dy


1 2
1
L L ıˆ   L2 L ˆ
L
L
2
2
 ıˆ  ˆ
2
L
2
2
0 0
Q4)
ıˆ  [( R ˆ)  (T1kˆ)  ( R ˆ)  (T2 kˆ)]  Iˆ 

ıˆ  [T1 Rıˆ  T2 Rıˆ]  Iˆ z1 / R
T1kˆ  m1 gkˆ  m1 z1kˆ


T1  m1 g  m1 z1
T2 kˆ  m2 gkˆ  m2 z2 kˆ
T  m g  m z
2
2 1
 2

 z1  R z2   R
(T2  T1 ) R  Iˆ z1 / R
(m2  m1 ) R 2

(m2  m1 ) gR  (m2  m1 ) z1R  I ˆ z1 / R
z1 
g
T1  m1 g  m1 z1
(m2  m1 ) R 2  I
T  m g  m z
2
2 1
 2
ˆ  M e  Iˆ 

 f1  m1a1

 f 2  m2 a2
Soluzioni Termodinamica
Q2)
  dU  dL
  ncV dT  pdV
dQ

 pV  nRT
T

T0
dT
R

T
cV
TV
R
cV
 Kost
V

V0
dV
V
0  ncV dT 
T
R V
ln   ln
T0
cV V0
nRT
dV
V
0  cV
R
V
T
ln  ln( 0 ) cV
T0
V
dT
dV
R
T
V
dT
R dV

T
cV V
R
V
T
 ( 0 ) cV
T0
V
TV
R
cV
R
cV
0 0
TV