Esercizio n. 8
Una lastra indefinita, di spessore
infinitesimo h, è poggiata sul piano xy
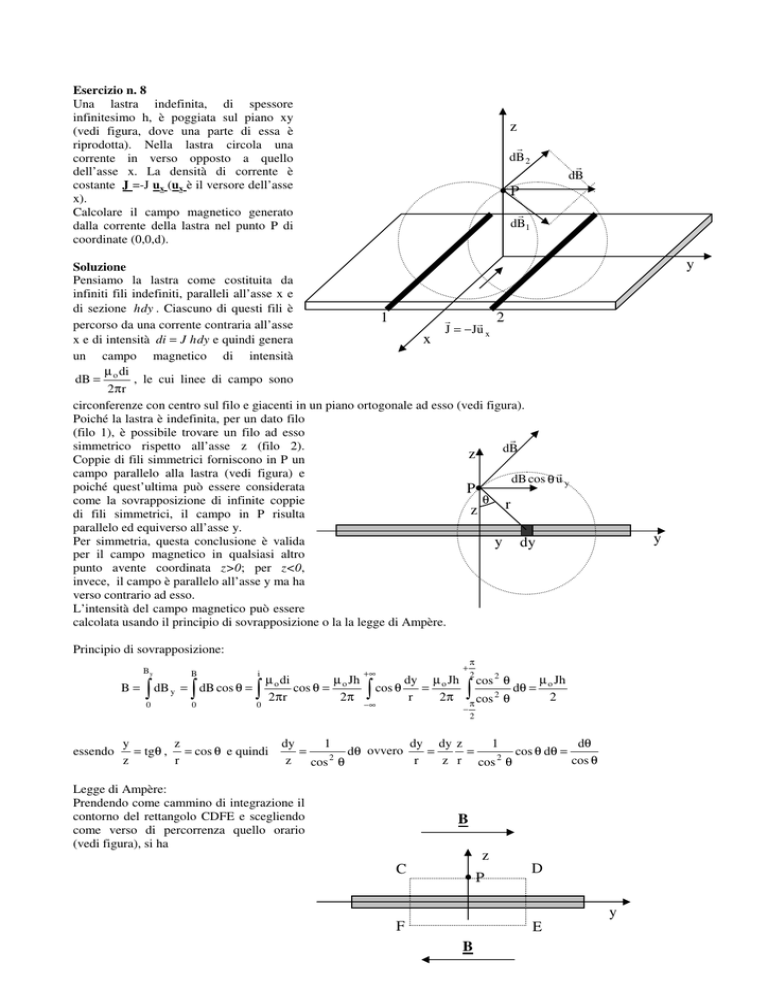
(vedi figura, dove una parte di essa è
riprodotta). Nella lastra circola una
corrente in verso opposto a quello
dell’asse x. La densità di corrente è
costante J =-J ux (ux è il versore dell’asse
x).
Calcolare il campo magnetico generato
dalla corrente della lastra nel punto P di
coordinate (0,0,d).
z
dB 2
dB
•P
dB1
y
Soluzione
Pensiamo la lastra come costituita da
infiniti fili indefiniti, paralleli all’asse x e
di sezione h dy . Ciascuno di questi fili è
1
2
percorso da una corrente contraria all’asse
J = − Ju x
x
x e di intensità di = J h dy e quindi genera
un campo magnetico di intensità
µ di
dB = o , le cui linee di campo sono
2π r
circonferenze con centro sul filo e giacenti in un piano ortogonale ad esso (vedi figura).
Poiché la lastra è indefinita, per un dato filo
(filo 1), è possibile trovare un filo ad esso
simmetrico rispetto all’asse z (filo 2).
dB
z
Coppie di fili simmetrici forniscono in P un
campo parallelo alla lastra (vedi figura) e
dB cos θ u y
poiché quest’ultima può essere considerata
P•
θ r
come la sovrapposizione di infinite coppie
z
di fili simmetrici, il campo in P risulta
parallelo ed equiverso all’asse y.
Per simmetria, questa conclusione è valida
y dy
per il campo magnetico in qualsiasi altro
punto avente coordinata z>0; per z<0,
invece, il campo è parallelo all’asse y ma ha
verso contrario ad esso.
L’intensità del campo magnetico può essere
calcolata usando il principio di sovrapposizione o la la legge di Ampère.
y
Principio di sovrapposizione:
By
B=
i
dB y = dB cos θ =
0
essendo
B
0
0
µ Jh
µ o di
cos θ = o
2π
2π r
y
z
= tgθ , = cos θ e quindi
z
r
+∞
cos θ
−∞
dy µ o Jh
=
r
2π
+
−
π
2
cos 2 θ
π cos
2
2
θ
dθ =
µ o Jh
2
dy
dy dy z
1
1
dθ
=
dθ ovvero
=
=
cos θ dθ =
2
2
z
θ
r
z
r
cos
cos θ
cos θ
Legge di Ampère:
Prendendo come cammino di integrazione il
contorno del rettangolo CDFE e scegliendo
come verso di percorrenza quello orario
(vedi figura), si ha
B
C
z
•P
F
D
E
B
y
C
B ⋅ ds = µ o i conc.
B=
2
E
F
B ⋅ ds + B ⋅ ds + B ⋅ ds + B ⋅ ds = 0 + B CD + 0 + B EF = 2 B CD = µ o J h CD
F
µo J h
D
C
D
E












