Macchina di Atwood
George Atwood mise a punto un apparato sperimentale per verificare le leggi del moto
uniformemente accelerato
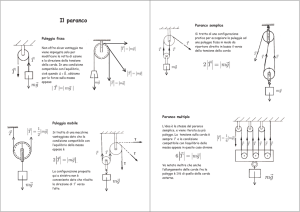
La macchina di Atwood è costituita da due masse m1 e m2 collegate con un filo
inestensibile di massa trascurabile posto sopra una puleggia di massa trascurabile. In
questo modo è possibile compiere delle misure comodamente perché l’accelerazione a di
caduta della massa più grande è minore di g. La macchina è dotata di un pendolo che
permette di misurare i tempi di caduta
Equazioni del moto
Sulla massa m1 agiscono il peso Q1 e la tensione del filo N
Sulla massa m2 agiscono il peso Q2 e la tensione del filo N
L’ equazione del moto sarà
π1 π − π − π2 π + π = (π1 + π2 )π
(1)
Da cui
π=
π1 − π2
π
π1 + π2
Viceversa, l'accelerazione di gravità g può essere trovata misurando lo spostamento dei
pesi, e ricavando l'accelerazione uniforme, dalla relazione
1
β = ππ‘ 2
2
ed inserendo il valore così trovato di a nella formula scritta nella pagina precedente.
Equazione della tensione
Dopo aver ricavato il valore dell'accelerazione si può trovare il valore della tensione N del
filo.
π1 π = π1 π − π
Da cui si ottiene
π −π
2π1 π2
π = π1 π (1 − π1 +π2 ) = π π
(2)
1
2
1 +π2
Caso della puleggia di massa non trascurabile
Se la puleggia ha una massa mc non trascurabile, rispetto a quelle dei due pesi m1 e m2 ,
e raggio r dobbiamo applicare i principi della meccanica del corpo che ruota.
Sulla puleggia agisce il momento (π1 − π2 )π; in realtà la differenza βN dipende dalla
massa del cavo ed in prima approssimazione è trascurabile se la massa del cavo è piccola
Possiamo scrivere il 2° principio della dinamica del moto rotatorio per la puleggia
(π1 − π2 )π = πΌπΜ
(3)
1
Essendo πΌ = 2 ππ π 2
e
1 ππ£
πΜ = π ππ‘ =
π
π
Si ricava
1
(π1 − π2 ) = ππ π
2
Tornando nella (1) ed inserendo il dato ricavato è
π1 π − π1− π2 π + π2 = π(π1 + π2 )
1
(π1− π2 )π − ππ π = π(π1+ π2 )
2
Ed infine
π=π
π1 − π2
1
π1 + π2 + 2 ππ
Procedendo come sopra si ricava la tensione del cavo
Caso della puleggia con attrito
Nel caso in cui la puleggia sia soggetta alla forza d'attrito, ma allo stesso tempo la sua
massa sia trascurabile rispetto alle masse dei pesi, la (1) verrà modificata aggiungendo la
forza d'attrito.
(4)
π1 π − π − π2 π + π − ππ = (π1 + π2 )π
Quindi
π=
(π1 − π2 )π − ππ
π1 + π2
Caso della puleggia di massa non trascurabile con attrito
Deducendo da quanto sopra esposto
π=
(π1 − π2 )π − ππ
1
π1 + π2 + 2 ππ
