Elettrotecnica (prof. G. Lupò) –Prova scritta del 9 luglio 2013
……/………………
(cognome)
.......................
ESERCIZIO N.1a
(nome)
.....................
(matricola)
[N47(M-Z)-N48-N50-535]
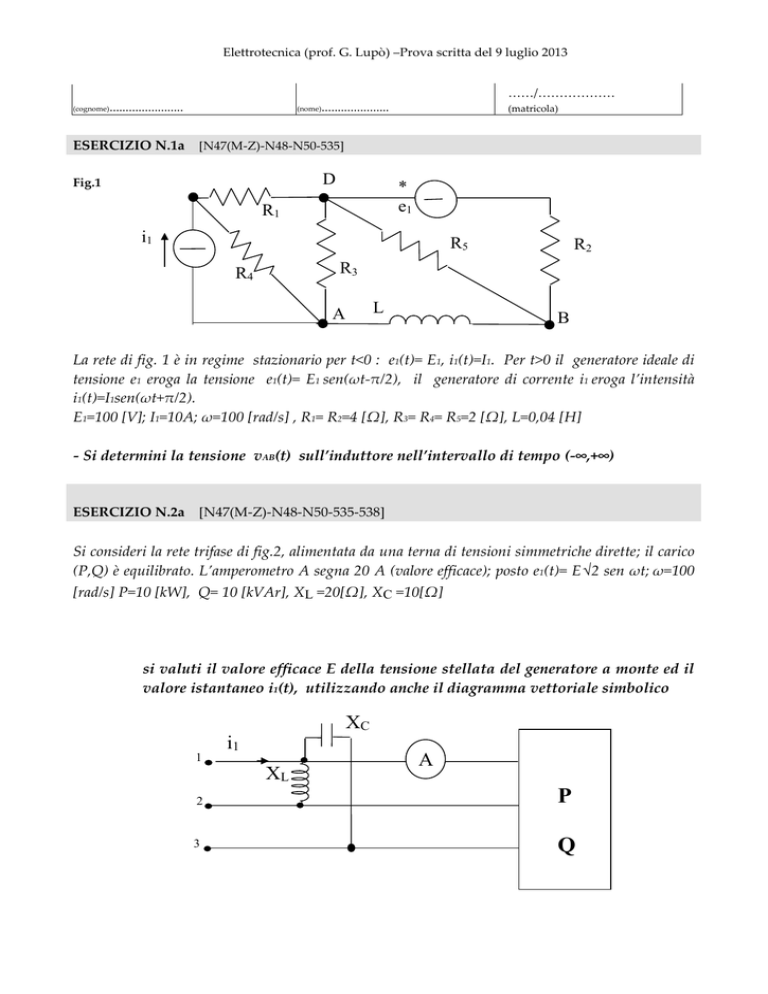
D
Fig.1
R1
*
e1
A
A
i1
R5
A
R3
R4
R2
A
A
A
L
A
B
A
A
A
La rete di fig. 1 è in regime stazionario per t<0 : e1(t)= E1, i1(t)=I1. Per t>0 il generatore ideale di
tensione e1 eroga la tensione e1(t)= E1 sen(ωt-π/2), il generatore di corrente i1 eroga l’intensità
i1(t)=I1sen(ωt+π/2).
E1=100 [V]; I1=10A; ω=100 [rad/s] , R1= R2=4 [Ω], R3= R4= R5=2 [Ω], L=0,04 [H]
- Si determini la tensione vAB(t) sull’induttore nell’intervallo di tempo (-∞,+∞)
ESERCIZIO N.2a
[N47(M-Z)-N48-N50-535-538]
Si consideri la rete trifase di fig.2, alimentata da una terna di tensioni simmetriche dirette; il carico
(P,Q) è equilibrato. L’amperometro A segna 20 A (valore efficace); posto e1(t)= E √2 sen ωt; ω=100
[rad/s] P=10 [kW], Q= 10 [kVAr], XL =20[Ω], XC =10[Ω]
si valuti il valore efficace E della tensione stellata del generatore a monte ed il
valore istantaneo i1(t), utilizzando anche il diagramma vettoriale simbolico
XC
i1
1
XL
A
2
P
3
Q
Elettrotecnica (prof. G. Lupò) –Prova scritta del 9 luglio 2013
ESERCIZIO N.1b [N47(M-Z)-N48-N50-535]
D
Fig.1
A
R1
*
A
e1
R4
R2
io
R3
i3
A
A
A
A
A
C
A
A
A
ic
B
A
A
La rete di fig. 1 è in regime stazionario per t<0 : e1(t)= E1, io(t)=Io. Per t>0 il generatore ideale di
tensione e1 eroga la tensione e1(t)= E1 cosωt,, il generatore io l’intensità di corrente io (t)= Io senωt.
E1=25 [V] ; Io =2A; ω=100 [rad/s] , R1= R2=4 [Ω], R3= R4=2 [Ω], C=5 [mF]
- Si determini l’intensità di corrente ic(t) e l’intensità di corrente i3(t) nell’intervallo di
tempo (-∞,+∞)
ESERCIZIO N.2b [N47(M-Z)-N48-N50-535-538]
Si consideri la rete trifase di fig.2, alimentata da una terna di tensioni simmetriche dirette; il carico
(P,Q) è equilibrato. L’amperometro A segna 20 A (valore efficace); posto e1(t)= E √2 sen ωt; ω=100
[rad/s] P=10 [kW], Q= -10 [kVAr], XL =20[Ω], XC =10[Ω]
si valuti il valore efficace E della tensione stellata del generatore a monte ed il
valore istantaneo i3(t), utilizzando anche il diagramma vettoriale simbolico
XC
1
2
A
P
XL
3
i3
Q












