19991119

Corso di Elettrotecnica DUM A.A. 1999/2000
Prova scritta del 19 novembre 1999
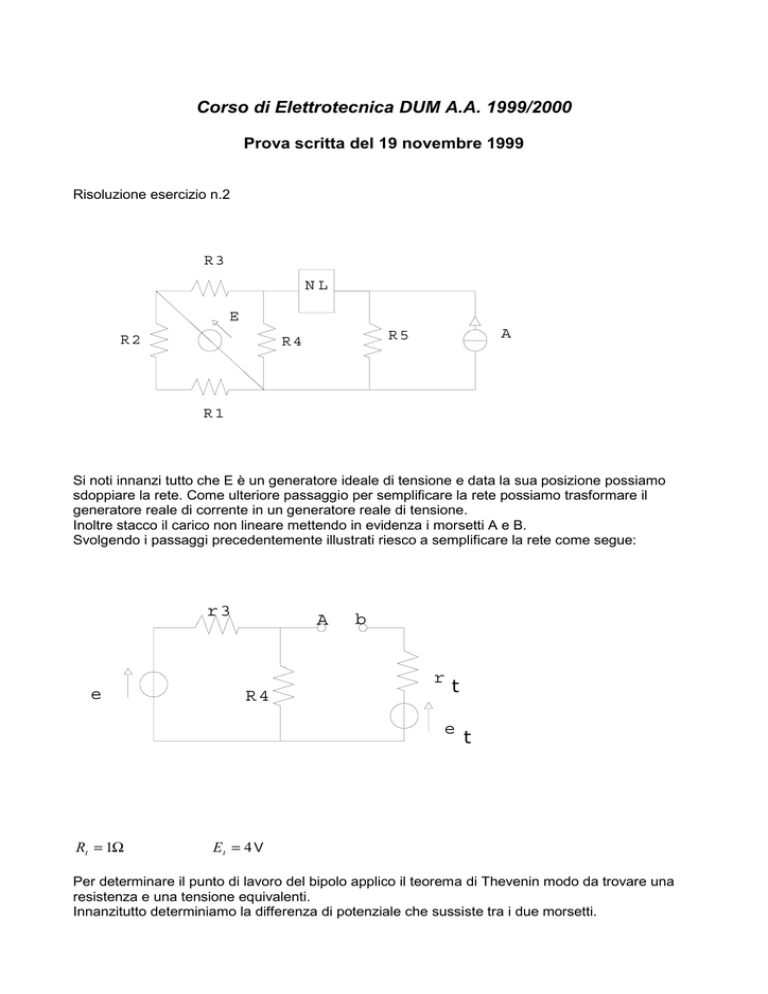
Risoluzione esercizio n.2
R3
NL
E
R2
A
R5
R4
R1
Si noti innanzi tutto che E è un generatore ideale di tensione e data la sua posizione possiamo
sdoppiare la rete. Come ulteriore passaggio per semplificare la rete possiamo trasformare il
generatore reale di corrente in un generatore reale di tensione.
Inoltre stacco il carico non lineare mettendo in evidenza i morsetti A e B.
Svolgendo i passaggi precedentemente illustrati riesco a semplificare la rete come segue:
r3
A
b
r
e
R4
t
e
Rt = 1Ω
t
Et = 4 V
Per determinare il punto di lavoro del bipolo applico il teorema di Thevenin modo da trovare una
resistenza e una tensione equivalenti.
Innanzitutto determiniamo la differenza di potenziale che sussiste tra i due morsetti.
Per fare ciò applico il principio della sovrapposizione degli effetti:
Faccio funzionare il 1° generatore spegnendo il 2°:
r3
b
rt
2
r4
1
e
a
La corrente prodotta non circola nel ramo dove è posta la resistenza RT , essendo questo un ramo
aperto, quindi la differenza di potenziale ai due morsetti coincide con la differenza di potenziale
che esiste ai capi della resistenza R4 .
Svolgendo i calcoli per trovare la differenza di potenziale cercata ottengo:
I=
E
16
=
=4 A
R 3 + R4 2 + 2
VR 4 = V i AB = I ⋅ R4 = 4 ⋅ 2 = 8 V
Faccio funzionare il 2° generatore spegnendo il 1°:
r3
A
b
r
r4
E
t
t
Le resistenze R3 e R4 sono in parallelo e hanno come risultante 1 Ω .
Nella maglia 2 non circola corrente perché è aperta per cui la tensione ai morsetti A e B risulta
opposta alla tensione prodotta dal generatore di tensione :
V ii AB = − Et = −4 V
Sovrapponendo gli effetti dei due generatori:
i
ii
V AB = V AB
+ V AB
=8−4 = 4 V
Ora passivo la rete e ricavo la resistenza equivalente:
r3
a
b
rt
r4
La resistenza Rt è in serie con il parallelo di R3 ed R4 :
R ⋅R
2⋅2
Req = Rt + 3 4 = 1 +
= 2Ω
R3 + R4
2+2
Il circuito equivalente risultante è il seguente:
nl
r
i
eq
eq
e eq
La corrente che circola nel circuito è:
E
4
I eq = eq = = 2 A
Req 2
Posso ricavare il punto di lavoro attraverso un procedimento grafico.
Il punto di intersezione fra le due rette è il punto di lavoro del bipolo non lineare che funziona con
un valore di tensione pari a 2 V e una corrente di 1 A.
I
2
2
4
V
Soluzione a cura di Francesco Manzoni