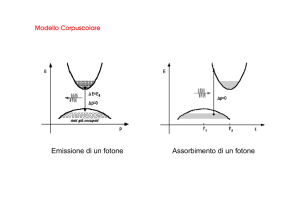
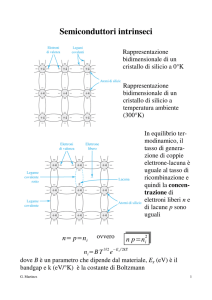
Struttura elettronica degli elementi
La natura quantizzata dell’elettrone deriva da quattro grandezze deterministiche
(misurabili sperimentalmente) che prendono nome di numeri quantici.
• Numero quantico principale n= 1(K), 2(L), 3(M), 4(N), 5(O), 6(P), 7(Q).
Il massimo numero di elettroni consentiti nella corteccia n è 2n2.
• Numero quantico momento angolare l= 0(sharp), 1(principal), 2(diffuse), 3(fundamental), …, n-1.
Il momento angolare determina la forma della nuvola elettronica.
La corteccia n ammette n sottocortecce: 0, 1, …, n-1.
• Numero quantico magnetico ml= 0, ±1, ±2, …, ±l.
Il numero quantico magnetico fornisce l’orientazione (orbitale) dei lobi delle sottocortecce.
Il numero di orientazioni ml relative alla sottocorteccia l è 2l+1
• Numero quantico spin ms= ±½.
Principio di esclusione di Pauli
In un sistema elettronico neppure due elettroni possono avere la stessa quaterna
di numeri quantici (n, l, ml, ms).
Struttura elettronica degli elementi
Struttura elettronica degli elementi
Elemento
Numero Atomico
Notazione Spettroscopica
C
6
1s2 2s2 2p2
Si
14
1s2 2s2 2p6 3s2 3p2
Ge
32
1s2 2s2 2p6 3s2 3p6 3s10 4s2 4p2
Sn
50
1s2 2s2 2p6 3s2 3p6 3s10 4s2 4p6 4d10 5s2 5p2
Struttura elettronica degli elementi
Elemento
Numero Atomico
Si
14
Notazione Spettroscopica
1s2 2s2 2p6 3s2 3p2
Consideriamo N atomi isolati.
In ciascun atomo isolato vi sono, negli ultimi due livelli, due elettroni nel livello s e due elettroni nel livello p.
2N elettroni che occupano i 2N possibili livelli s alla stessa energia
2N elettroni che occupano un terzo dei 6N possibili livelli p alla stessa energia
Quando gli atomi si accoppiano per formare il cristallo, le funzioni d’onda atomiche si sovrappongono ed il cristallo
(sistema elettronico) deve obbedire al principio di esclusione di Pauli.
I 2N stati s ed i 6N stati p, inizialmente alla stessa energia, degenerano per assumere energie diverse. Tali energie sono
molto prossime tra loro dal momento che N è un numero molto grande ~51022 cm-3.
Nella condizione di equilibrio i 4N stati occupati da elettroni (2N di tipo s e 2N di tipo p) sono degenerati in un’unica banda
denominata Banda di Valenza.
Analogamente i 4N stati privi di elettroni (4N di tipo p) sono degenerati nella Banda di Conduzione.
Le due bande sono separate dalla Banda Proibita.
La distribuzione delle bande di energia caratterizza le proprietà di conducibilità del materiale
Bande di energia in un materiale
n ~ 1022 e/cm3
Energy gap ~ 6eV (Carbonio)
n ~ 10 e/cm3
Energy gap ~ 1eV
n ~ 1010 e/cm3
Bande di energia nel silicio
Reticolo cristallino
Legame covalente
Bande di energie
Allo zero assoluto tutti gli elettroni sono contenuti nella banda di valenza e
la banda di conduzione è completamente vuota.
Generazione di una coppia elettrone-lacuna
Reticolo cristallino
Legame covalente
Bande di energie
A temperatura ambiente alcuni legami covalenti si rompono ad opera
dell’energia termica fornita al cristallo creando coppie elettrone-lacuna.
Sia gli elettroni in banda di conduzione che le lacune in banda di valenza
partecipano al meccanismo della conduzione elettrica (bipolarità).
In un semiconduttore intrinseco il numero di elettroni in banda di conduzione è
pari al numero di lacune in banda di valenza.
n = p =ni
Conduzione elettrica
Meccanismo con cui una lacuna partecipa alla conduzione.
E’ un meccanismo che non coinvolge gli elettroni liberi.
Gli elettroni e le lacune possono essere trattate, ai fini della conduzione
elettrica, come particelle classiche fittizie aventi massa efficace mn e mp.
Approssimazione valida se i campi esterni sono assai più deboli di quelli
periodici prodotti dalla struttura reticolare.
La massa efficace ci consente di ignorare per i portatori liberi (elettroni e
lacune) la dipendenza del reticolo cristallino.
Corrente di drift
v n = − µn E
v p = µ pE
J n = − qnv n
J p = qnv p
J = ( nµn + pµ p ) qE = σE
σ = q(nµn + pµ p )
ρ=
1
σ
La mobilità è funzione del tempo medio tra due urti consecutivi e della
massa efficace del portatore
Corrente di diffusione
dn
xˆ
dx
dp
J p = −qD p xˆ
dx
Dn Dp KT
=
=
= VT
µn µ p
q
J n = qDn
K = 8.62 ⋅ 10−5 eV / Κ
Corrente totale
dn
xˆ
dx
dp
J p = qpµ p E − qDp xˆ
dx
ITOT = A(J n + J p )
J n = qnµ n E + qDn
Densità degli stati nei semiconduttori
La densità di stati gC(E) fornisce il numero di stati per unità di volume e per unità
di energia consentiti agli elettroni in banda di conduzione in corrispondenza
del livello energetico E.
Analogamente la grandezza gV(E) fornisce il numero di stati per unità di volume
e per unità di energia consentiti alle lacune in banda di valenza in
corrispondenza del livello energetico E.
La densità degli stati fornisce un’informazione sul numero di stati consentiti e
non sulla loro effettiva occupazione da parte dei portatori liberi.
8π 2 2 3 2
gC ( E ) =
mn E − EC
3
h
8π 2 2 3 2
gV ( E ) =
m p EV − E
3
h
Maggiore (minore) è il livello energetico E rispetto ad EC (EV) e maggiore è il
numero di stati consentiti.
Funzione di distribuzione Fermi-Dirac
La funzione di distribuzione Fermi-Dirac f(E) fornisce la probabilità che un
elettrone occupi uno stato quantico ad un livello energetico E.
f (E) =
1
⎛ E − EF ⎞
1 + exp⎜
⎟
⎝ KT ⎠
EF rappresenta il livello di Fermi ovvero il livello in cui la probabilità di
trovare un elettrone è ½.
Analogamente la probabilità che una lacuna occupi uno stato quantico
ad energia E è 1-f(E).
Funzione di distribuzione Fermi-Dirac
Variazione della funzione Fermi-Dirac con la temperatura
EC + EV 3KT ⎛ m p ⎞
EF = Ei =
ln⎜⎜ ⎟⎟
+
2
4
⎝ mn ⎠
Concentrazione dei portatori intrinsici
L’effettiva concentrazione di elettroni liberi al livello energetico E si ottiene
moltiplicando il numero degli stati consentiti gC(E) per la probabilità f(E) che
tali stati siano effettivamente occupati.
n(E)=gC(E)f(E) analogamente p(E)= gV(E)(1-f(E))
n=
∫ n( E )dE = ∫ g
BC
BC
C
( E ) f ( E )dE
p=
∫
BV
p( E )dE =
∫g
V
BV
( E )(1 − f ( E ))dE
Concentrazione dei portatori intrinsici
n = ∫ n( E )dE = ∫ g C ( E ) f ( E )dE
BC
p=
BC
∫
BV
p ( E )dE = ∫ gV ( E )(1 − f ( E ))dE
BV
n = p = ni ≈ 1.5 ⋅ 1011 cm −3 T = 300Κ
np = ni2
Legge di azione di massa
⎛ E ⎞
ni2 = BT 3 exp⎜⎜ − g ⎟⎟
⎝ KT ⎠
B = 5.4 ⋅ 1031
La concentrazione intrinseca non dipende da EF ma dalla temperatura e dalle
proprietà del materiale.
Donatori e accettori
Silicio intrinseco
Silicio drogato di tipo n
Silicio drogato di tipo p
n ≈ ND
p ≈ NA
⎛ EF − Ei ⎞
n = ni exp⎜
⎟
⎝ KT ⎠
⎛ Ei − EF ⎞
p = ni exp⎜
⎟
⎝ KT ⎠
Donatori e accettori
n ≈ ND
p ≈ NA
⎛ E − Ei ⎞
n = ni exp⎜ F
⎟
KT
⎝
⎠
⎛ E − EF ⎞
p = ni exp⎜ i
⎟
KT
⎝
⎠
nn ≈ N D
ni2
pn =
nn
Diagramma a bande in presenza di polarizzazione
L’applicazione di un potenziale V all’estremità destra del cristallo comporta
una crescita lineare del potenziale all’interno del cristallo e,
conseguentemente, una diminuzione lineare delle bande di energia.
La variazione del diagramma a bande è qV.
d (energia _ potenziale )
dx
1 dEi
E=
q dx
− qE = −
Giunzione p-n all’equilibrio termodinamico
Consideriamo due regioni di materiale
semiconduttore, una di tipo p e l’altra di tipo
n, uniformemente drogate e fisicamente
separate.
Il livello di Fermi EF è prossimo al bordo della
banda di valenza nel semiconduttore di tipo
p, analogamente, l’elevata concentrazione
di elettroni nel semiconduttore di tipo n
sposta il livello di Fermi EF verso il bordo della
banda di conduzione.
Quando le due regioni costituiscono una
giunzione p-n, il forte gradiente di
concentrazione dei portatori liberi provoca
la diffusione di lacune dal lato p verso
quello n ed, analogamente, la diffusione di
elettroni dalla regione n verso quella p.
Giunzione p-n all’equilibrio termodinamico
Le lacune che diffondono dal lato p verso
quello n lasciano in prossimità della
giunzione ioni negativi NA- non compensati.
Analogamente, nel lato n restano vicino
alla giunzione ioni positivi ND+ non
compensati.
Di conseguenza si forma, a ridosso della
giunzione, una regione di carica spaziale
negativa nel lato p ed una regione di
carica spaziale positiva nel lato n. Nasce
un campo elettrico diretto dalla carica
positiva verso quella negativa e, pertanto,
una corrente di drift che si oppone alla
diffusione dei portatori.
In condizioni di equilibrio termodinamico il
flusso netto di corrente è nullo e la corrente
di drift eguaglia quella di diffusione.
Giunzione p-n all’equilibrio termodinamico
Concentrazione dei portatori.
Distribuzione della carica spaziale.
Distribuzione del campo elettrico.
Andamento del potenziale.
-xp
xn
⎛N N ⎞
2ε s ⎛ 1
1 ⎞
⎟⎟Vbi
⎜⎜
Vbi = φi = φ (x ) − φ (− x ) = VT ln⎜⎜ A 2 D ⎟⎟ W = xn + x p =
+
n
q
N
N
⎝ A
D ⎠
⎝ i ⎠
n
p
Potenziale di barriera
Regione di svuotamento
ε s = 1.04 ⋅ 10−12 F / cm
Giunzione p-n in polarizzazione inversa
Quando una tensione di polarizzazione inversa Va è applicata alla giunzione, si osserva una
debole corrente inversa che scorre nel circuito esterno. Tale corrente è dovuta ad elettroni e
lacune generati termicamente ed è pertanto indipendente dal valore della tensione
applicata (purché inferiore del valore di breakdown). In tale condizione si ha un
allargamento della regione di svuotamento ed un incremento della barriera di potenziale
I = IS
Giunzione p-n in regione di breakdown
Quando la tensione di polarizzazione inversa Va eccede un valore di soglia VZK la corrente
che scorre nel circuito esterno cresce molto rapidamente in quanto si innesca un
meccanismo di breakdown che rende disponibile un numero elevato di portatori.
Il meccanismo di breakdown può essere dovuto a due effetti.
• Effetto zener – il campo elettrico nella regione di svuotamento è talmente elevato (campo
elettrico critico) da rompere i legami covalenti e generare coppie elettrone-lacuna.
• Moltiplicazione a valanga – un portatore che attraversa la regione di svuotamento, sotto
l’azione del campo elettrico, acquisisce un valore di energia cinetica sufficiente a rompere
un legame covalente in seguito ad un urto con il reticolo cristallino. I portatori liberati da
questo processo possono a loro volta acquisire energia cinetica sufficiente a liberare altri
portatori e così via. Si genera, in tal modo, una valanga di portatori che incrementa
notevolmente il valore della corrente inversa.
Giunzione p-n in polarizzazione diretta
In polarizzazione diretta, si ha una riduzione del
potenziale di barriera per cui la corrente di diffusione
predomina su quella di drift. Le lacune potranno
diffondere dal lato p verso quello n ed essere raccolte
al morsetto negativo della batteria, analogamente, gli
elettroni potranno diffondere dal lato n verso il lato p
ed essere raccolti al morsetto positivo della batteria.
Giunzione p-n in polarizzazione diretta
V
VT
pn ( xn ) = pno e ;
V
VT
n p ( − x p ) = n po e ;
Legge della giunzione
pn ( x ) = pno + ( pn ( xn ) − pno )e
− ( x − xn )
Lp
n p ( x ) = n po + (n p ( − x p ) − n po )e
Lp = D pτ p ;
x+ x p
Ln
Ln = Dnτ n .
Giunzione p-n in polarizzazione diretta
⎞
⎛ VV
Dp
dp
T
⎜
J p = − qD p
pno e − 1⎟e
=q
⎟
⎜
dx
Lp
⎠
⎝
− ( x − xn )
Lp
;
⎞
⎛ VV
Dn
T
⎜
n po e − 1⎟e
Jn = q
⎟
⎜
Ln
⎠
⎝
x+ x p
Ln
;
V
V
V
⎛
⎞
⎛
⎞
⎛
⎞
⎛ Dp
⎞
⎛
⎞
D
D
D
p
VT
VT
VT
2
n
n
⎜
⎟
⎜
⎟
⎜
⎟ e − 1 = I S e − 1⎟.
+
p +
n ⎟ e − 1 = Aqni ⎜
I = Aq⎜
⎜ L no L po ⎟⎜
⎜
⎟⎜
⎟
⎟
⎜
⎟
L
N
L
N
n
p
D
n
A
⎝ p
⎠⎝
⎝
⎠⎝
⎝
⎠
⎠
⎠
Andamento delle varie componenti di corrente trascurando meccanismi di generazionericombinazione all’interno della regione di svuotamento.
Caratteristica di una giunzione p-n
Capacità offerte da una giunzione p-n
Alle estremità della regione di svuotamento sono presenti due distribuzioni di carica uguali
ed opposte. La regione di svuotamento si presenta pertanto come un condensatore la cui
capacità è funzione della tensione applicata.
E’ possibile mostrare che la capacità offerta dalla regione di svuotamento è assimilabile a
quella di un condensatore a facce piane e parallele,
CW =
εs A
W
in cui A è la sezione del semiconduttore e W è l’ampiezza della regione di svuotamento.
Quando la giunzione è polarizzata direttamente, si crea un eccesso di portatori minoritari
nelle regioni neutre. La relativa quantità di carica varia con la tensione diretta applicata e
fa assumere alla giunzione un comportamento capacitivo.
CD =
τI
VT