Conduttivita': legata al trasporto di carica nel cristallo
Elettrone: Pacchetto d'onde → Vel. elettrone = Vel. di gruppo
1
∇k ε
ℏ
dv
dk m* d 2ε d (ℏk )
→ F = m*a = m*
= m* ∇k v
= 2
dt
dt
ℏ dk 2 dt
∇ v ,∇ v , ∇ v
→ v = ∇k ω =
k x
p = ℏk
m*
dp →
F = ℏ 2
dt
−1
1
→ ( m* ) = 2
ℏ
2
2
d ε
d ε
≡
2
dk
dki dk j
k y
k z
∇k v
d 2ε
=1
dk 2
d 2ε
, m* massa efficace
2
dk
grandezza con 9 componenti: tensore di massa efficace
Significato:
ai =
1 d 2ε
Fj → Caso generale: a
ℏ 2 dki dk j
F
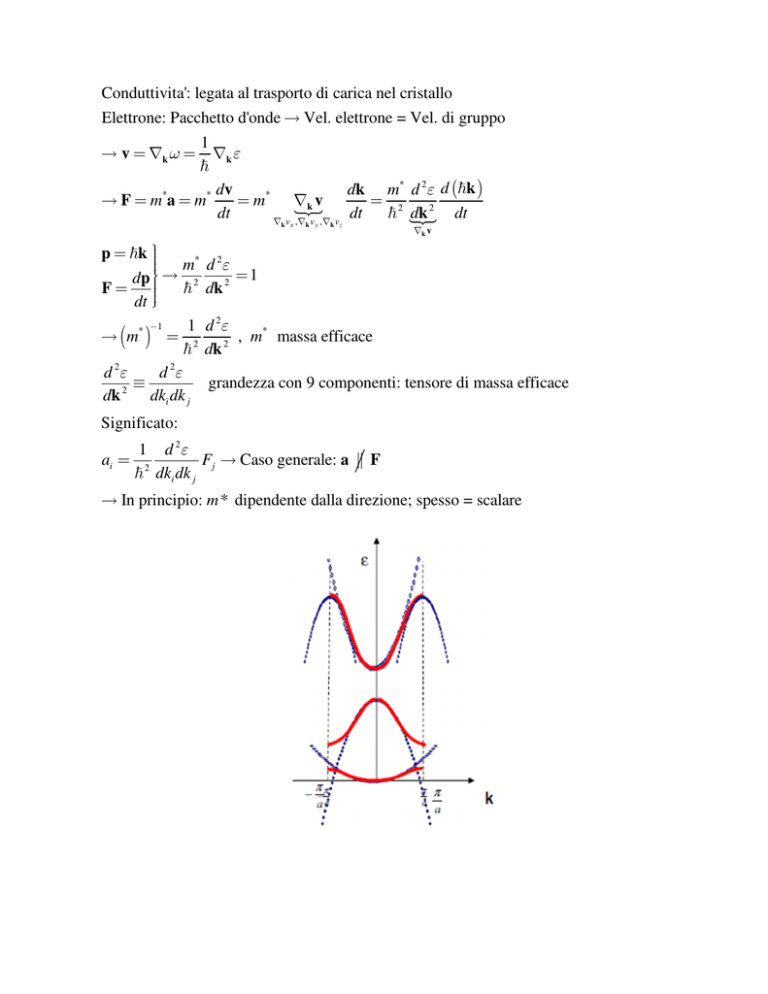
→ In principio: m * dipendente dalla direzione; spesso = scalare
Rel di dispersione in approssimazione parabolica :
m* indipendente da k
Ek = E (k 0 ) +
dE
dk
⋅ (k − k 0 ) +
k0
1 d 2E
2 dk 2
2
(k − k 0 ) ≈ E (k0 ) +
k0
ℏ2
2
( k − k0 )
2m *
=0
(minimo)
m* =
ℏ2
→ Segno di m * legato a concavita' → ± !!
d 2E
dk 2 k
0
Massa efficace negativa: concetto difficile da maneggiare
Azione di un campo esterno:
F = q (E + v × B ) = m * a → a =
q
(E + v × B )
m*
→ Ridefiniamo:
m* → m *
→ Relazione fra F e a invariata
q → ±q secondo il segno ± di m *
q > 0 : lacuna = stato vuoto in una banda permessa
→ Moto portatori in un potenziale periodico:
elettroni in BC
lacune in BV
Confronto fra osservabili in modelli alla Sommerfeld e alla Bloch
Popolamento delle bande: T = 0 K
2N elettroni in b.valenza, 0 elettroni in b. conduzione
Isolanti & Semiconduttori
Corrente di banda piena:
Esempio caso 1D:
q
∑ vi = 0
L i
i
Per ogni elettrone con + vi ce n'e' un altro con − vi
I = jA = ρ A∑ vi = −
Popolamento delle bande: T > 0 K
Attivazione termica di elettroni da BV a BC
Effetto di un campo elettrico:
Shift verso stati a en. piu' alta
→ Perdita della compensazione delle velocita' → I1 , I 2 ≠ 0
Elettroni mobili in BV:
Quelli che contribuiscono a I stessa v di quelli in BC
v=
dE
dk
Vel. banda di conduzione
Vel. banda di valenza
Lacune: quasi-particelle con carica positiva
Elettroni
Lacune
Origine dell'idea di lacuna:
q
q
q
IV = − ∑ vi = + ∑ vi − ∑ vi = + ∑ vi
L stati
L tutti
L stati
stati
gli stati
occupati
occupati
vuoti
Infatti:
∑
vi = 0
banda piena
Tutti
gli stati
Esempi piu' casalinghi di lacune:
Movimento del 'buco' : opposto al movimento del 'pieno'
Concentrazioni di elettroni/lacune:
Banda di conduzione o di valenza
n(E) = g (E) f (E)
g ( E ) densita' degli stati per intervallo unitario di energia
f ( E ) probabilita' di occupazione di uno stato di energia E
g ( E ) , p ( E ) indipendenti
G (k ) dk = 2
V
3
( 2π )
G (k )
4πk 2 dk
densita' degli stati per intervallo unitario di energia
k2
g (k ) dk =
dk = 2 dk come sopra, per unita' di volume
π
V
2 2
dE ℏ 2 k
ℏ k
E = Ec +
→
= *
2m*
dk
m
g (k ) k 2 m*
g ( E ) dE = g (k ) dk → g ( E ) =
= 2 2
dE
π ℏ k
dk
1
k 2 m*
1
m*
k=
2m* ( E − Ec ) → g ( E ) = 2 2 = 2 2m* ( E − Ec ) 2
π ℏ k πℏ
ℏ
ℏ
32
→ g (E) =
(2m* )
2π 2 ℏ 3
E − Ec
32
gC ( E ) =
( 2 m* )
2π 2ℏ 3
E − EC dens. stati nella banda di conduzione
32
gV ( E ) =
( 2 m* )
2π 2ℏ 3
EV − E dens. stati nella banda di valenza
Probabilita' di occupazione: Distribuzione di Fermi-Dirac
f (E) =
g
1+ e
E − EF
kT
, g molteplicita', EF livello di Fermi












