Semiconduttori intrinseci
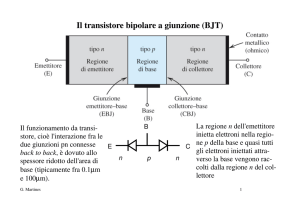
Rappresentazione
bidimensionale di un
cristallo di silicio a 0°K
Rappresentazione
bidimensionale di un
cristallo di silicio a
temperatura ambiente
(300°K)
In equilibrio termodinamico, il
tasso di generazione di coppie
elettrone-lacuna è
uguale al tasso di
ricombinazione e
quindi la concentrazione di
elettroni liberi n e
di lacune p sono
uguali
n= p=n i
ovvero
2
n p=ni
n i =B T 3/2 eE / 2kT
dove B è un parametro che dipende dal materiale, Eg (eV) è il
bandgap e k (eV/°K) è la costante di Boltzmann
g
G. Martines
1
Semiconduttori drogati
Materiale di tipo n:
• il drogante è tipicamente fosforo
• la concentrazione dei donori ND è normalmente
maggiore di ni e quindi
2
n
pn ≈ i
ND
n n≈ N D
• i portatori maggioritari sono gli elettroni
NOTA:
nel silicio a 300°K ni =1,5×10
22
5×10 atomi/cm3
G. Martines
10
per cm3 mentre ci sono
2
Semiconduttori drogati
Materiale di tipo p:
• il drogante è tipicamente boro
• la concentrazione dei donori NA è normalmente
maggiore di ni e quindi
2
p p≈ N A
n
n p≈ i
NA
• i portatori maggioritari sono le lacune (hole)
NOTA:
• le equazioni valgono in condizioni di equilibrio
termodinamico
• il materiale di tipo n o p resta elettricamente neutro per la
presenza delle cariche fisse (nuclei dei donori o accettori)
G. Martines
3
La corrente di deriva (drift)
In presenza di un campo elettrico E, elettroni e lacune
vengono accelerati in direzioni opposte e acquistano una
velocità data rispettivamente da
v ndrift =µ n E
v pdrift =µ p E
le costanti µp e µn prendono il nome di mobilità delle
lacune e degli elettroni. Il flusso di cariche determina le
correnti:
I p = Aqp µ p E
I n = Aqnµ n E
dove A è l'area della sezione, q la carica dell'elettrone, p ed
n le concentrazioni di lacune e di elettroni liberi.
I S = I p+ I n
Nota: le mobilità di lacune ed elettroni non sono uguali.
Nel Si, µp = 480 cm2/Vsec e µn= 1350 cm2/Vsec
G. Martines
4
La corrente di diffusione (ID)
La densità di corrente
di diffusione è
espressa da
dp( x)
J p =qD p
dx
dove la diffusività
delle lacune Dp (o
coefficiente di
diffusione) è una
costante che dipende
dal materiale mentre la
derivata è il gradiente
di concentrazione.
dn( x)
dx
NOTA: nel silicio Dp = 12 cm2/s e Dn = 35 cm2/s
Analogamente per gli elettroni: J n =qD n
La relazione di Einstein lega diffusività e mobilità
Dn D p
µ n = µ p =V T
kT
T
≈
è la tensione termica
q 11600
NOTA : a 300°K, VT ~ 25,9 mV
dove V T =
G. Martines
5
Giunzione pn a circuito aperto
Regione di svuotamento o regione di carica spaziale
V 0=V T ln(
Na ND
2
i
n
)
nota come barriera di potenziale o tensione di built-in
G. Martines
6
Giunzione pn polarizzata
G. Martines
7
Giunzione pn polarizzata direttamente
Profili a regime della concentrazione dei portatori minoritari in una giunzione pn polarizzata
direttamente nella ipotesi che sia NA>>ND.
G. Martines
8
Giunzione pn polarizzata direttamente
Profili delle concentrazioni nel materiale n
al bordo della regione di carica spaziale: p n ( x n )= pn0 e
V /V T
la concentrazione in eccesso vale:
pn ( x n ) pn0 = p n0 (e
V /V T
1)
e decade esponenzialmente con la distanza per effetto della
V /V
( x x )/ L
ricombinazione: pn ( x) pn0 = p n0 (e 1)e
T
n
p
Lp = lunghezza di diffusione delle lacune nel materiale n.
La corrente di diffusione nel materiale tipo n
più piccola è LP => più rapidamente le lacune iniettate si
ricombinano con gli elettroni liberi => più rapidamente si
riduce la concentrazione dei portatori minoritari => più
intensa è la corrente di diffusione dei portatori minoritari
(aumenta il gradiente) => i portatori maggioritari (gli
elettroni liberi) persi per la ricombinazione, vengono
rimpiazzati da eletroni esterni alla regione n => si genera
una corrente di elettroni
Il massimo della densità di corrente di diffusione si ha per
Dp
V /V
x= x n e vale J p ( x n )=q
pn0 (e
1) e poi decresce
Lp
esponenzialmente come la concentrazione in eccesso.
La densità di corrente dei maggioritari cresce come
decresce quella dei minoritari e quindi la somma delle
correnti resta costante nel materiale n e pari al massimo di
Jp.
( )
G. Martines
T
9
Giunzione pn polarizzata direttamente
La corrente di diffusione nel materiale tipo p
il meccanismo è del tutto analogo per gli elettroni nel
materiale tipo p (sono portatori minoritari)
il massimo della densità di corrente di diffusione si ha per
Dn
V /V
x=x p e vale J n (x p )=q
n p0 (e 1)
Ln
( )
T
la somma delle densità di corrente resta costante anche nel
materiale di tipo p e pari al massimo di Jn
La corrente nella giunzione pn :
Nella regione di svuotamento le densità di corrente di
diffusione non cambiano valore.
I = A( J p + J n )= Aq
2
i
I = Aqn
(
(
)
Dp
D
V /V
p n0 + n n p0 (e 1)
Lp
Ln
)
T
Dp
Dn
V /V
V /V
+
(e 1)= I S (e 1)
L p N D Ln N A
T
T
IS è la corrente di saturazione o di scala
NOTA: l'equazione vale anche per V < 0 e I tende a -IS .
NOTA: IS dipende fortemente dalla temperatura (come ni2)
G. Martines
10
Caratteristica V-I della giunzione pn
I = I S (e
G. Martines
V /V T
1)
11
Breakdown della giunzione pn
Effetto Zener: generazione di coppie elettrone-lacuna nella
regione di svuotamento per effetto dellintensità del campo
elettrico che spezza i legami covalenti
Effetto valanga: gli elettroni accelerati dal campo elettrico
nella regione di svuotamento acquisiscono una energia
sufficiente non solo a ionizzare gli atomi ma a generare
elettroni capaci di ionizzare altri atomi
L'effetto Zener prevale per VZ < 5V
L'effetto valanga prevale con VZ > 7V
G. Martines
12
Capacità di giunzione Cj
È associata alla carica immagazzinata nella regione di
svuotamento quindi è rilevante in polarizzaione inversa
√
Q j= A 2 s q
NANd
(V 0 +V R)
N A+ N D
la carica dipende da VR in modo non lineare.
Si definisce in modo incrementale:
∣ ∣
C j=
G. Martines
dQ j
dV R V
R
=V Q
13
Capacità di diffusione Cd
É dovuta alla carica associata all'accumulo di portatori
minoritari nell'intorno della regione di svuotamento di un
giunzione pn polarizzata direttamente.
Definendo il tempo di vita dei portatori minoritari τ
come il tempo medio prima della annichilazione del
portatore di carica, cioè
2
L
τ p= p per le lacune nel materiale n
Dp
2
L
τ n= n per gli elettroni nel materiale p
Dn
la carica può essere espressa da
Q=τ p I p +τ n I n =τ T I
con τΤ detto tempo di transito medio
La capacità di diffusione incrementale può essere espressa
da
τ
dQ
Cd = = T I
dV
VT
( )
G. Martines
14
Sommario giunzione pn
G. Martines
15