CAPITOLO 2
FUNZIONI e INSIEMI NUMERICI
FUNZIONI
Dati due insiemi A e B, si dice funzione da A a B ogni legge che ad ogni elemento di A fa
corrispondere o associa un solo elemento di B.
Scriveremo
f : A → B o anche
f
A ⎯
⎯→
B.
Se A , B ⊆ R , possiamo dare una rappresentazione grafica alla funzione.
Ad esempio
fi : R → R i = 1 , 2
f1 ( x ) = 2 x
f2 ( x ) = x2
L’insieme A è detto dominio e si indica con D f, mentre l’insieme
{ y∈ B
},
: y = f ( x) , x ∈ A
ossia l’insieme dei valori f ( x ) al variare di x in A, è detto
codominio e si indica con C f.
Se ad elementi distinti di A corrispondono elementi distinti di B, la funzione si dice iniettiva (la
funzione f1 è iniettiva, f2 non lo è).
Se C f = B, la funzione si dice suriettiva su B ( f1 è suriettiva su R, f2 non lo è).
Se
f : A → B è iniettiva e suriettiva si dice biunivoca o biiettiva (o corrispondenza biunivoca).
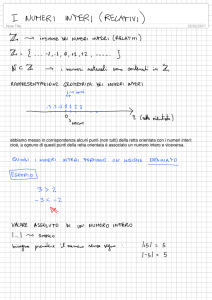
INSIEMI NUMERICI
Gli insiemi numerici sono i seguenti:
{1 , 2 , 3 , ... , n , ... }
{ 0 , ± 1, ± 2 , ... , ± n , ...}
•
numeri naturali
N =
•
numeri interi
Z =
•
numeri razionali
⎧ m
⎫
Q = ⎨
con m , n ∈ Z , n ≠ 0⎬ .
⎩ n
⎭
Osserviamo che per i numeri razionali si può dare una rappresentazione decimale e che vale la
uguaglianza 0 , 999999999….. = 1.
Presa una retta r, fissati su essa due punti distinti O ed A (si è così individuato il verso positivo da O
verso A e il segmento unitario OA),
5
è possibile associare ad ogni numero razionale un punto di r, il punto B corrisponde al numero
m
m
> 0 se la misura di OB è
. Ma su r rimangono dei punti che non corrispondono a
n
n
nessun numero razionale, infatti il punto P tale che il segmento OP è congruente alla diagonale OC
del quadrato di lato OA non corrisponde a nessun numero razionale ossia
non esiste
m
m
∈Q :
= OP con m e n primi tra loro.
n
n
Infatti dovrebbe essere OP = OC : OC2 = OA2 + AC2 = 2 o anche
m2
= 2 ,
n2
m 2 = 2 n 2 ma questa uguaglianza è impossibile.
Si introduce allora un nuovo insieme numerico che contenga Q e che consenta di riempire i buchi,
tale insieme è l’insieme dei numeri reali R.
Definizione assiomatica di R
Sull’insieme R sono definite due operazioni (addizione e moltiplicazione) che godono delle
proprietà :
a + b = b + a , a ⋅b = b⋅a , ∀ a ,b∈ R
1) commutativa
2) associativa
a + (b + c ) = ( a + b ) + c , a ⋅ (b ⋅ c ) = ( a ⋅ b ) ⋅ c , ∀ a ,b,c ∈ R
3) distributiva
a ( b + c ) = a ⋅ b + a ⋅ c , ∀ a ,b,c ∈ R
4) esistenza elementi neutri
a+0= a ,
a ⋅1 = a , ∀ a ∈ R
5) esistenza opposto e reciproco a + (− a ) = 0 , ∀ a ∈ R ; a ⋅ a − 1 = 1 , ∀ a ≠ 0 .
Su R è definita una relazione d’ordine ( ≤ ) che gode delle proprietà:
6) di ordine totale
∀ a , b ∈ R si ha a ≤ b oppure b ≤ a
a≤b e b≤c ⇒a≤c
7)
transitiva
8)
antisimmetrica
a≤beb≤a ⇒a= b
9) a ≤ b ⇒ a + c ≤ b + c
10)
a≤bec>0 ⇒ a⋅c≤b ⋅c
Vale l’assioma di completezza
11)
∀ A , B ⊆ R con A , B ≠ Φ e a < b , ∀ a ∈ A e ∀ b ∈ B
e ∀b ∈B.
6
allora ∃ c ∈ R : a ≤ c ≤ b ∀ a ∈ A
(osserviamo che il precedente assioma può essere proposto anche in formulazioni diverse da quella
qui data).
Osservazioni :
•
in N non c’è lo zero ne’ l’opposto
•
in Z non c’è il reciproco
•
in Q non vale l’assioma di completezza
(esempio
A=
{ x ∈Q
+
}
: x2 ≤ 2 , B =
{ x ∈Q
+
}
: x2 > 2
non esiste
c ∈Q : a ≤ c ≤ b , ∀ a∈ A e ∀ b ∈ B ) .
E’ possibile definire una corrispondenza biunivoca tra l’insieme R ed i punti di una retta r .
Ora ci occupiamo del seguente problema :
quanti sono gli elementi di N , Z , Q , R ?
Per rispondere al precedente quesito ricorriamo al concetto di corrispondenza biunivoca.
Definizione di infinità numerabile :
si dice che l’insieme A è una infinità numerabile (o semplicemente numerabile o che ha la potenza
del numerabile) se esiste una corrispondenza biunivoca tra l’insieme N ed A.
Sono insiemi numerabili :
P (insieme dei pari) , D (insieme dei dispari) , Z , Q.
Si dimostra che R non è numerabile.
Definizione di insieme continuo :
si dice che l’insieme A è un continuo ( o che ha la potenza del continuo) se esiste una
corrispondenza biunivoca tra l’insieme R ed A.
Ad esempio A =
{x
∈ R : − 1 < x < 1} è continuo
f : R → A è biunivoca
1
Intervalli e semirette
-1
Introduciamo ora particolari sottoinsiemi di R.
Dati
a , b ∈ R con a < b chiamiamo intervalli di estremi a e b gli insiemi
7
{x
[ a , b ] =
∈ R : a ≤ x ≤ b}
{x
]a , b ] =
(intervallo chiuso)
∈ R : a < x ≤ b}
] a , b [ =
{x
∈ R : a < x < b} (intervallo aperto)
[ a , b [ =
{x
∈ R : a ≤ x < b}
e semirette gli insiemi
[a , +∞[ =
{x
∈ R : x ≥ a}
]a , +∞[ =
{x
∈ R : x > a}
]−∞,b[ =
{x
∈ R : x < b}
]− ∞ , b ] =
{x
∈ R : x ≤ b}
CAPITOLO 3
L’ INSIEME C DEI NUMERI COMPLESSI
I NUMERI COMPLESSI
Si dice insieme dei numeri complessi, e si indica con C, la totalità delle coppie ordinate ( a , b )
con
a,b ∈R
con le seguenti regole di calcolo
(a , b ) + ( c , d ) = ( a + c , b + d )
( a , b) ⋅ ( c , d ) = ( a c − b d , a d
+ b c) .
Si dimostra che valgono le usuali proprietà delle operazioni.
Osserviamo che è possibile definire una corrispondenza biunivoca tra C e l’insieme dei punti di un
piano sul quale sia stato considerato un sistema di riferimento cartesiano
P
b
a
(al numero ( a , b ) si associa il punto P di coordinate cartesiane
( a , b ) ) dunque come R è
rappresentato dai punti di una retta, C è rappresentato dai punti di un piano che viene detto piano di
Gauss.
Vediamo ora alcune importanti conseguenze delle regole di calcolo date su C.
Si ha ( a , b ) = ( a , 0 ) + ( 0 , b ), dunque studiamo anzitutto i numeri del tipo
( a , 0 ).
8
Essi vengono rappresentati sulla retta orizzontale r inoltre somma e prodotto di numeri con seconda
coordinata nulla è ancora un numero con seconda coordinata nulla infatti, per le regole date, si ha
(a,0) + (c,0) = ( a + c , 0)
( a,0) (c,0) = ( ac - 0,a0+0c) = ( ac,0)
(sono gli unici punti che stanno su una retta del piano di Gauss a godere di questa proprietà).
Per tali punti è allora sufficiente dare la prima coordinata, possiamo dunque introdurre la seguente
identificazione
(a,0) ≡a
(tramite questa identificazione possiamo affermare che vale la proprietà
R ⊆C ).
Consideriamo ora i numeri del tipo ( 0 , b ) .
Essi stanno sulla retta verticale i. Per le regole date si ha
( 0 , b ) = ( 0 , 1 ) (b , 0)
123
≡b
dunque il numero ( 0 , 1 ) genera tutti gli altri, per questo viene indicato con un simbolo particolare,
si pone
(0,1) = i
(unità immaginaria)
e si ha allora
( 0 , b ) = ( 0 , 1 ) ( b , 0) = i b,
dunque, ricordando le uguaglianze precedenti, otteniamo
a , b ∈ R (forma algebrica di un numero
( a , b ) = ( a , 0 ) + ( 0 , b ) = a + i b con
complesso).
Proprietà dell’unità immaginaria :
i2 = (0,1)(0,1) = (-1,0) = -1
i3 = (-1,0)(0,1) = (0,-1) = -i
i4 = 1
i5 = i …
Per eseguire i calcoli con numeri in forma algebrica si usano le usuali regole dell’ algebra
trasformando le eventuali potenze del numero i nei rispettivi valori.
Esempi :
1) ( a + i b ) ( c + i d ) = a c + i a d + i b c + i 2 b d = (poiché i 2 = - 1)
= ac+iad+ibc–bd = (ac - bd) + i(ad+bc)
2) ( a + i b )2 = a2 + 2 i a b + i2 b2 = ( a2 - b2 ) + 2 i a b.
Notazioni : dato il numero complesso
z = ( a , b ) = a + i b si pone
9
a = R e z ( parte reale)
(attenzione
,
b = I m z (coefficiente della parte immaginaria)
a , b ∈ R !).
Complesso coniugato : dato z = a + i b , si dice suo coniugato z , il numero
ossia si ha
z = a − i b,
Re z = Re z , I m z = − I m z .
z + z = 2a ∈ R ,
Proprietà :
Reciproco di z ≠ 0 : dato
z ⋅ z = a 2 − i 2 b 2 = a 2 + b 2 ∈ R.
z = a + i b (con a e b non contemporaneamente nulli ossia
a 2 + b 2 ≠ 0 ) cerchiamo
a−ib
1
1
a
b
=
=
.
= 2
−i 2
2
( a + i b) ( a − i b )
z
a + ib
a + b
a + b2
Forma trigonometrica
Dato il numero z = a + i b, ad esso corrisponde un solo punto P ≡ ( a , b ) sul piano complesso
(o piano di Gauss). La posizione del punto P può essere univocamente determinata non solo dalle
sue coordinate cartesiane ma anche dalla sua distanza dal punto 0 (origine degli assi) e dall’angolo
(a meno di multipli interi di
2 π) che la retta orizzontale r forma con la retta OP.
P
O
r
Distanza di P da O = modulo = ρ (numero reale non negativo, il modulo di z si indica con | z |),
angolo = argomento = θ (a meno di 2 k π , ∀ k ∈ Z ) (sono le coordinate polari di P).
Si dice argomento principale quello che sta in [ 0 , 2 π [ (abitualmente prenderemo questo).
Formule di trasformazione :
⎧ a = ρ cos θ
⎨
⎩ b = ρ sin θ
,
⎧ ρ = a2 + b2
⎪
a
b
⎪
, sin θ =
se ρ ≠ 0
⎨ θ : cos θ =
ρ
ρ
⎪
⎪
⎩
se ρ = 0 , (cioè P ≡ O ) si pone θ qualunque.
Potremo allora scrivere : z = a + i b = ρ ( cos θ + i sin θ ) (forma trigonometrica).
Uguaglianza :
dati zr = ρr ( cos θr + i sin θr ) , r = 1 , 2 si ha z1 = z2 sse
ρ1 = ρ2 e ∃ k ∈ Z : θ1 - θ2 = 2 k π.
Prodotto in forma trigonometrica
10
Dati zr = ρr ( cos θr + i sin θr ) , r = 1 , 2 si ha
z1 z2 = ρ1 ρ2 [ cos ( θ1 + θ2 ) + i sin ( θ1 + θ2 ) ]
(ossia il modulo di un prodotto è dato dal prodotto dei moduli e l’argomento di un prodotto è dato
dalla somma degli argomento dei fattori)
infatti
z1 z2 = ρ1 ρ2 ( cos θ1 cos θ2 + i cos
=
θ1 sin θ2 + i sin θ1 cos θ2 - sin θ1 sin θ2) =
ρ1 ρ2 [ cos ( θ1 + θ2 ) + i sin ( θ1 + θ2 ) ] (per le formule di addizione).
FORMULE DI EULERO
Per ogni x ∈ R vale la seguente identita’ e i x = cos x + i sin x . Da essa si deduce che
e − i x = cos x − i sin x e, sommando e sottraendo membro a membro le due identita’ scritte, si
ottengono le seguenti due formule cos x =
ei x + e− i x
ei x − e − i x
, sin x =
.
2
2i
Dalla prima identita’ si ha pure la seguente uguaglianza e 2 k π = 1 , ∀ k ∈ Z .
Ancora utilizzando la prima identita’, dato il numero complesso z scritto in forma trigonometrica
ossia z=ρ ( cos θ + i sin θ ) , possiamo scrivere z = ρ e i θ ; questa e’ detta forma
esponenziale del numero complesso z.
FORMULA DI DE MOIVRE
Dati
z = ρ ( cos θ + i sin θ ) e n ∈ N, si ha la seguente formula (detta di De Moivre)
z n = ρ n ( cos n θ + i sin n θ ).
RADICI n – sime di un numero complesso
Dati un numero complesso α = ρ0 ( cos θ0 + i sin θ0 ) ( con 0 ≤ θ0 < 2 π ) e
n ∈ N ( n ≥ 2 ), cerchiamo z ∈ C (se ce ne sono! ) tali che z n = α .
Scriviamo z in forma trigonometrica z = ρ ( cos θ + i sin θ ) (con ρ e θ incognite) allora
z n = ρ n ( cos n θ + i sin n θ ) dunque
zn = α
⇔
ρ n ( cos n θ + i sin n θ ) = ρ0 ( cos θ0 + i sin θ0 )
11
⇔
⎧ ρn = ρ0
⎨
⎩nθ =θ 0 + 2 k π
⎧ ρ = n ρ0
⎪
⎨
θ0 + 2 k π .
⎪ θ =
n
⎩
⇔
Le soluzioni del precedente problema hanno stesso modulo (
n
ρ 0 ).
Si sono trovati infiniti
argomenti, ma quanti di essi individuano numeri complessi distinti?
Si dimostra che per k = 0 , 1 , …, n – 1 si ha 0 ≤ θ =
θ0 ≥ 0 ⇒
θ0 + 2 k π
θ0 + 2 k π
n
< 2 π infatti
≥ 0 ovviamente, mentre
n
θ 0 < 2 π , k ≤ n − 1 ⇒ θ 0 + 2 k π < 2 π + 2 ( n − 1 ) = 2 n π da cui
θ0 + 2 k π
2n π
= 2π .
n
<
n
Dunque, per tali valori di k, si hanno numeri complessi distinti (sono n valori).
Si può provare che per gli altri valori di k si ottengono argomenti che differiscono da uno dei
precedenti per un multiplo intero di 2 π .
Consideriamo, ad esempio due casi :
per k = 0 si ha
per k = n si ha
θ0 + 2 k
=
n
θ0 + 2 k π
n
=
θ0
,
n
θ0
n
+
θ
2nπ
= 0 + 2π
n
n
dunque i due argomenti differiscono per 2 π .
In conclusione le radici n-sime del numero α = ρ0 ( cos θ0 + i sin θ0 ) sono i numeri
complessi z = ρ ( cos θ + i sin θ ) :
ρ =
n
ρ0
θ =
,
θ0 + 2 k π
n
, k = 0 ,1, .... , n − 1 .
Proprietà del modulo
1)
| z 1 z 2 | = | z 1 | | z2 | (dimostrata)
2)
z1
z1
=
z2
z2
1)
z1 + z
infatti se
2
≤
se
z2 ≠ 0 ,
z1 + z
2
(disuguaglianza triangolare)
z 1 = a 1 + i b 1 e z 2 = a 2 + i b 2 , considerati i punti P i ≡ ( a i , b i ) , si ha
12
P
P2
P1
P ≡ ( a 1 + a 2 , b 1 + b 2 ) poiché
P1Q = OR e PQ = P1R , dunque
| z 1 | = OP1 , | z 2 | = OP2 = P1P , | z1 + z 2 | = OP
e nel triangolo OPQ si ha
OP ≤ OP1 + P1 P da cui la tesi.
13