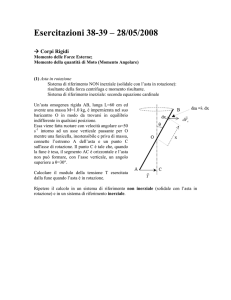
Un’asta omogenea ha lunghezza l, spessore trascurabile e massa ma.
Ad una sua estremità è fissato un disco omogeneo di raggio r e massa md,
mentre l’altra estremità è vincolata ad un asse ortogonale al piano della
figura e passante per il punto O, asse attorno al quale l’asta può
ruotare con attrito trascurabile nel piano verticale.
L’asta, che si trova inizialmente nella posizione d’equilibrio instabile,
ad un dato istante comincia a cadere in seguito a una lieve perturbazione.
Determinare le espressioni delle seguenti grandezze:
a) il momento d’inerzia totale IO del sistema rispetto all’asse orizzontale passante per O.
b) la coordinata yG del centro di massa del sistema nella condizione iniziale di equilibrio instabile.
c) la massima velocità angolare ωmax assunta dal sistema in funzione di ma , md, IO , yG e del
modulo dell’accelerazione di gravità g.
il momento d’inerzia rispetto al centro di massa di una asta omogenea di massa ma
1
e lunghezza l e’ I CM = ma l 2 mentre il momento d’inerzia rispetto al punto O
12
1
risulta essere I O = ma l 2
in effetti secondo il teorema di Huygens Steiner
3
il momento d’inerzia di un corpo esteso di massa totale ma calcolato rispetto
a
ad un asse che si trova a distanza d
da un asse passante per il centro di massa
e’ dato da
quindi
=
I I C + ma d
2
percio’ se
I CM a
1
= ma l 2
12
1
l2
2
=
IO a
ma l + ma
12
4
1
I O = ma l 2
3
il momento d’inerzia rispetto al centro di massa di un disco omogeneo di massa md
e’ pari a
I CM d =
1
md r 2
2
dunque il momento d’inerzia del disco omogeneo
rispetto al punto O sara’ dato da
I Od =I CM d + md ( l + r ) =
2
1
2
2
md r + md ( l + r )
2
in conclusione il momento d’inerzia totale sara’
I OT =
1
1
2
ma l 2 + md r 2 + md ( l + r )
3
2
per quanto riguarda la seconda domanda dato che la massa ma e’ distribuita in modo omogeneo
lungo l’asta e che la massa md e’ distribuita in modo omogeneo sul disco la coordinata yG del
centro di massa del sistema nella condizione iniziale di equilibrio instabile si otterra’
considerando che la massa dell’asta puo’ essere pensata come concentrata nel suo centro di
massa posto a distanza l/2 dal punto O mentre quella del disco puo’ essere pensata come
concentrata nel centro del disco posto a distanza ( l + r ) da O
ma l / 2 + md ( l + r )
yG =
(ma + md )
infine ωmax si avrà nella posizione di energia potenziale minima (θ = π);
applicando la conservazione dell’energia meccanica e la relazione tra energia potenziale della
forza peso e quota del centro di massa si ha
energia potenziale iniziale = (ma + md ) g yG
1
2
I OT ωmax
energia cinetica finale =
2
1
2
energia m. finale =
I OT ωmax
−(ma + md ) g yG
2
energia potenziale finale = −(ma + md ) g yG
energia m. iniziale = (ma + md ) g yG
energia cinetica iniziale = 0
data l’assenza di attriti possiamo imporre la conservazione dell’energia meccanica
(ma + md) g yG = (1/2)I0t (ωmax)2 - (ma + md)g yG
ωmax = [ 4(ma + md)g yG / I0t ] ½
da cui
Backup slides