Politecnico di Milano
Fondamenti di Meccanica– Esame del 10.02.2009
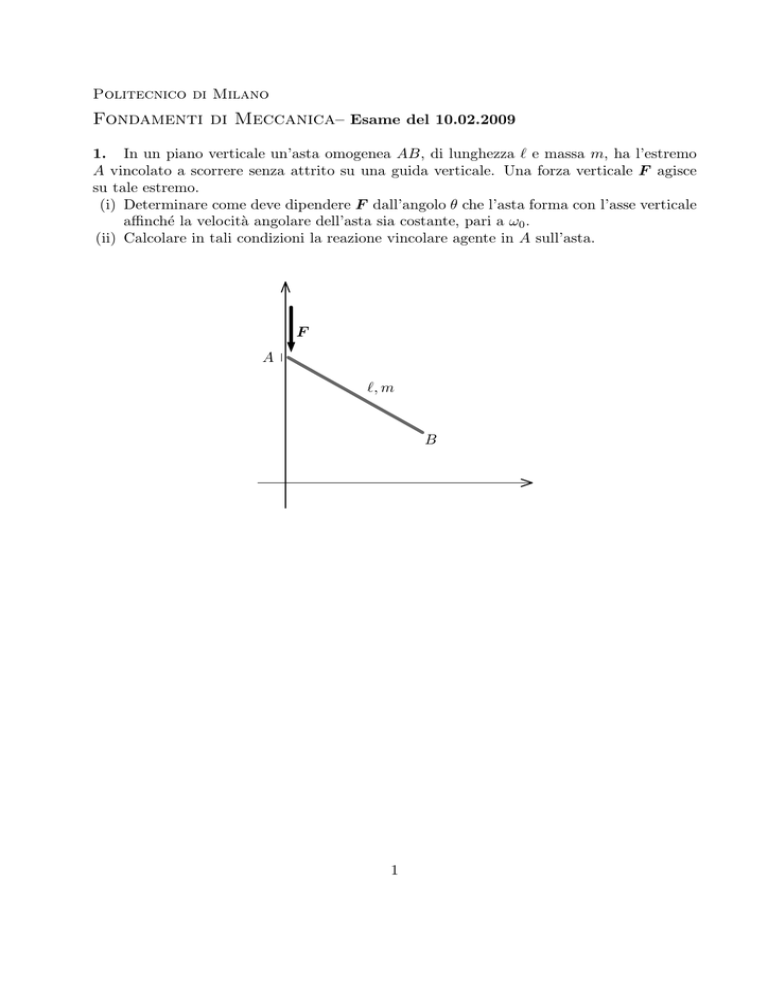
1. In un piano verticale un’asta omogenea AB, di lunghezza ℓ e massa m, ha l’estremo
A vincolato a scorrere senza attrito su una guida verticale. Una forza verticale F agisce
su tale estremo.
(i) Determinare come deve dipendere F dall’angolo θ che l’asta forma con l’asse verticale
affinché la velocità angolare dell’asta sia costante, pari a ω0 .
(ii) Calcolare in tali condizioni la reazione vincolare agente in A sull’asta.
F
A
ℓ, m
B
1
MECCANICA APPLICATA ALLE MACCHINE
Allievi meccanici AA.2008-2009 prova del 08-07-2009
Problema N.1
FB
OB=2L
OA=AC=L
B
M, JA
ac
Vc
A
C
FC
fD
O
Mc
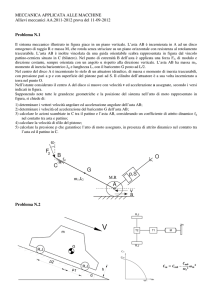
Il sistema articolato in figura, posto nel piano verticale, è composto dall’asta OB (massa M e
momento di inerzia baricentrico JA) e dall’asta AC (priva di massa) collegata ad OB mediante una
cerniera in A. All’estremo B dell’asta OB agisce in direzione verticale la forza nota FB. All’estremo
C dell’asta AC agisce una forza incognita FC ed è posta una massa concentrata MC. La guida
orizzontale del punto C è caratterizzata da un coefficiente di attrito di strisciamento fD. Sia
assegnata la posizione angolare dell’asta OB, espressa tramite l’angolo . Sono altresì assegnate la
velocità VC e l’accelerazione aC del punto C, con i versi indicati in figura. Si richiede di ricavare:
velocità ed accelerazione angolare dell’asta OB;
la forza Fc corrispondente al moto assegnato;
la reazione vincolare in corrispondenza della cerniera O.
Problema N.2
M 2 sin
M3
R, ,
D,
JM
R
H
Cm
Cm
Co 1
m
o
H
R2, M2, J2
F
M3
fv, fD, fA
M
Il sistema in figura è costituito da un motore (caratterizzato da una coppia Cm di cui è fornita
l’espressione della curva caratteristica e da un momento di inerzia JM), che aziona una puleggia di
raggio R tramite una trasmissione (rapporto di trasmissione e rendimenti D e R). Sulla puleggia
si impegna una fune considerata inestensibile, priva di massa e di diametro trascurabile, alle cui
estremità sono connessi da un lato un disco (raggio R2 massa M2 e momento di inerzia baricentrico
J2), e dal lato opposto una massa M3, secondo lo schema di figura, con M2 sin > M3.
Il disco rotola senza strisciare su un piano inclinato dell’angolo , ed il contatto con il piano è
caratterizzato da una resistenza al rotolamento (parametro fv), mentre fD e fA sono rispettivamente i
coefficienti di attrito di strisciamento e di aderenza tra disco e piano inclinato. Al centro del disco è
applicata una forza F. Si richiede di ricavare:
l’accelerazione del disco allo spunto, in salita;
1
MECCANICA APPLICATA ALLE MACCHINE
Allievi meccanici AA.2008-2009 prova del 08-07-2009
per la condizione precedente, la tensione nella fune in corrispondenza della sezione H-H;
la velocità di regime del centro del disco, sempre in salita;
il tempo necessario affinché il sistema abbia velocità nulla, a partire dalla condizione di regime,
in cui si annulli la coppia motrice.
Problema N.3
M, J
k1
k2
R1 = 2R2 =2R
R1
R2
C
k1 = 2k2 = 2k
J = (1/2)MR12
=2 o
Il sistema vibrante sopra raffigurato è costituito da due dischi tra loro solidali, aventi
rispettivamente raggi R1 e R2, mentre M e J sono rispettivamente la massa ed il momento di inerzia
dell’insieme dei due dischi. Due molle di rigidezza k1 e k2 sono collegate al corpo tramite fili
inestensibili, privi di massa e di diametro trascurabile che si avvolgono sulle circonferenze dei due
dischi. Sul disco è applicata una coppia nota pari a C=C0cos( t). Si richiede di ricavare, utilizzando
i legami indicati a lato nella figura e nell’ipotesi di puro rotolamento senza resistenza (parametro
fv=0):
la pulsazione naturale o del sistema;
l’ampiezza del moto a regime.
2
MECCANICA APPLICATA ALLE MACCHINE
Allievi meccanici AA.2008-2009 prova del 20-07-2009
Problema N.1
AB=BC=CD
= cost.
Il meccanismo in figura è posizionato nel piano verticale, la sola piastra BC è dotata di massa. Una
coppia resistente Mr è applicata all’asta CD. Per la posizione del sistema assegnata si chiede di
determinare:
i) la velocità del baricentro G e la velocità angolare della piastra BC;
ii) l’accelerazione del baricentro G e l’accelerazione angolare della piastra BC;
iii) la coppia Mm da applicare alla manovella AB per garantire il moto.
Problema N.2
Del veicolo in figura è nota la massa totale M, il raggio ed il momento d’inerzia di ogni singola
ruota (2 ruote per asse) ed il momento d’inerzia di un volano oltre alle dimensioni indicate in figura.
Il volano è collegato all’asse delle ruote posteriori attraverso una trasmissione a cinghia di
2 /1 assegnati. Il piano inclinato è scabro ed il
rendimento D / R e rapporto di riduzione
2 / 3
1
MECCANICA APPLICATA ALLE MACCHINE
Allievi meccanici AA.2008-2009 prova del 20-07-2009
contatto è caratterizzato da un coefficiente di attrito statico, radente e volvente rispettivamente fs, fr
ed fv.
Supponendo di trascurare la resistenza aerodinamica si chiede di:
i) calcolare l’accelerazione del veicolo in discesa.
ii) verificare l’aderenza delle ruote posteriori.
Problema N.3
Il sistema in figura si trova nella sua posizione di equilibrio. Un’asta di massa m e lunghezza L è
appoggiata su due dischi omogenei di raggio R. Nel punto di contatto tra asta e disco non vi è
strisciamento. L’asta è collegata a terra con un elemento elastico-dissipativo di caratteristiche note.
Inoltre sul disco di centro O’ è avvolta una fune che non può strisciare ed è collegata a terra con un
secondo elemento elastico dissipativo. Al disco di centro O è applicata una coppia nota di
espressione pari a C C0 cos t Assumendo la rotazione come coordinata libera si chiede di
determinare:
i) l’equazione di moto del sistema
ii) la frequenza del moto libero non smorzato
iii) la risposta a regime.
2
MECCANICA APPLICATA ALLE MACCHINE
Allievi meccanici AA.2008-2009 prova del 8-9-2009
Problema N.1
Del sistema meccanico riportato in figura sono note tutte le quantità geometriche riportate, ed è
posizionato nel piano verticale. Il disco omogeneo di centro C rotola senza strisciare sulla guida
curvilinea, tale disco è il solo corpo dotato di massa M e momento di inerzia baricentrico J.
Si consideri il sistema nell’istante in cui l’asta AB è in posizione orizzontale, nota la portata in
ingresso nella camera del cilindro QIN=cost, si richiede:
1. determinare velocità e accelerazione del centro del disco C;
2. determinare tramite un bilancio di potenze la pressione nel cilindro necessaria a garantire il
moto del sistema;
3. calcolare le reazioni vincolari in A.
h
h
Problema N.2
L’impianto di sollevamento riportato in figura è posto nel piano verticale. Le dimensioni
geometriche note sono quelle indicate in figura, inoltre sono note masse e momenti d’inerzia di tutti
i corpi. La curva caratteristica del motore è di tipo lineare, con equazione Cm=Co(1- m/ s).
Si richiede di:
4. determinare l’accelerazione allo spunto della massa m2 in salita, sotto l’ipotesi di moto
diretto;
5. determinare la velocità della massa m1 in salita a regime;
6. calcolare il tiro della fune nella sezione h-h, nella condizione del punto 1;
7. indicare quale relazione deve sussistere tra la massa m1 e la massa m2 affinché il moto sia
retrogrado a regime, con m1 in salita.
C(t)
Problema N.3
Il sistema in figura si trova nella sua posizione di equilibrio, sono note le masse e la geometria del
sistema. Assumendo la rotazione della puleggia p come coordinata libera, si richiede di
determinare:
8. l’equazione di moto del sistema
9. la frequenza del moto libero;
10. la risposta a regime essendo C(t)=C0eiΩt.