ESERCIZI DI FISICA GENERALE – nr. 16/07
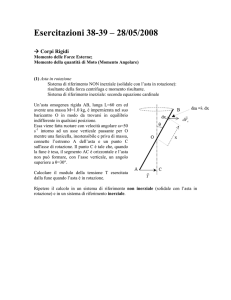
1. Un cavaliere medievale, di massa complessiva M = 500 Kg,
percorre un ponte levatoio, di materiale omogeneo, lunghezza l =
5.00 m, e massa m = 100 Kg, che è incernierato senza attriti ad
l
un suo estremo, mentre all’altro estremo è fissato tramite una
F
g
catena inestensibile (di massa trascurabile) alle pareti del
castello, in un punto che si trova ad una distanza verticale l =
θ
5.00 m al di sopra del perno (vedi figura). Per lo svolgimento del
x
problema, considerate il cavaliere (con cavallo e armatura) come
l
un punto materiale.
a) Detta x la coordinata del cavaliere lungo il ponte levatoio, come si scrive la funzione F(x) che
rappresenta la dipendenza del modulo della tensione della catena con la posizione x?
F(x) = ………………………………………..
(Mg x + mgl/2)/(l sinθ) , essendo θ =
45 gradi l’angolo rappresentato in figura
b) Sapendo che il carico massimo che la catena può sopportare prima di spezzarsi vale in modulo F’
= 5000 N,quanto vale la coordinata x’ a cui arriva il cavaliere prima che succeda il disastro?
x’ = …………………………………... = ……… m
F’l sinθ / (Mg) – ml / (2M) = 3.11 m
[risolvendo l’equazione scritta sopra per x e considerando una forza pari a F’
c) Tenendo conto che il ponte levatoio è ben approssimato da un’asta omogenea che ruota attorno ad
un asse passante per una sua estremità, quanto vale l’accelerazione angolare α del ponte subito
dopo la rottura della catena? [Se proprio non volete calcolarvelo, ricordate che il momento di
inerzia di un’asta omogenea di massa m e lunghezza l vale, in questo caso, I = ml2/3]
α = …………………………………... = ……… rad/s2
(mgl/2 + Mgx’)/I = 21.2 rad/s2
[dalla legge del moto di rotazione di un corpo rigido, tenendo conto che, subito dopo la rottura della catena, i momenti delle forze sono
solo quelli dovuti alla forza peso del ponte, applicata al suo centro di massa, e del cavaliere, applicata con un braccio pari a x’]
d) Il cavaliere comincerà a cadere verso il basso, ed il ponte a compiere una rotazione. Inizialmente
(subito dopo la rottura della catena), quanto valgono in modulo le accelerazioni lineari A ed a
rispettivamente del cavaliere e dell’estremità del ponte?
A = …………………………………... = ……… m/s2
g = 9.80 m/s2 [è un grave in caduta libera!]
a = …………………………………... = ……… m/s2
α l = 106 m/s2
[>> g !!]
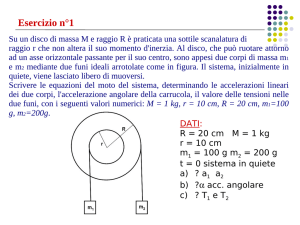
2. Il sistema materiale di figura è costituito da tre corpi puntiformi identici di massa m =
0.60 kg, tenuti insieme da un sistema di aste rigide di massa trascurabile. Nel
Y
m
sistema di riferimento indicato in figura, i tre corpi giacciono sul piano z = 0 e si
trovano rispettivamente nelle posizioni r1 = (-d,-d), r2 = (0, d), r3 = (d,-d), con d = 30
-d
d
X
cm. [Notate che i tre corpi si trovano ai vertici di un triangolo isoscele
m -d
m
“indeformabile”]
a. Qual è la posizione rCM = (xCM, yCM) del centro di massa del sistema?
xCM= …………………………………… = ………… m (m1x1+m2x2+m3x3)/(m1+m2+m3) = 0
[come si poteva vedere dal fatto che l’asse Y è un asse di simmetria del sistema]
yCM= …………………………………… = ………… m
0.10 m
(m1y1+m2y2+m3y3)/(m1+m2+m3)=-d/3=-
b. Quanto vale il momento di inerzia I0 per una rotazione del sistema attorno all’asse Z?
I0 = …………………………………… = ………… kg m2 m1r12+m2r22+m3r32=
m1(x12+y12)+m2(x22+y22)+m3(x32+y32)= 5md2 = 0.27 kg m2
c. Quanto vale il momento di inerzia I’ per una rotazione del sistema attorno ad un asse parallelo
all’asse Z e passante per la posizione del corpo 1?
I’ = …………………………………… = ………… kg m2 m1r’12+m2r’22+m3r’32=
m1((x1
–
x1)2+(y1 –y1)2)+ m2((x2 –x1)2+(y2 –y1)2)+ m3((x3 –x1)2+(y3 –y1)2)= 0 + m25d2 + m34d2 = 9md2 = 0.49 kg
m2 [notate che la massa 1 non “contribuisce” al momento di inerzia, dato che la sua distanza dall’asse di rotazione, r’1, è
in questo caso nulla; tuttavia I’>I0 dato che le masse m2 ed m3 vengono a trovarsi relativamente distanti dall’asse di
rotazione]
Francesco Fuso – tel 050 2214305 – e-mail: [email protected] – web page: http://www.df.unipi.it/~fuso/dida
d. Quanto vale il momento di inerzia ICM per una rotazione del sistema attorno ad un asse parallelo
all’asse Z e passante per la posizione del centro di massa? [Ricordate che potete anche usare il
“teorema degli assi paralleli”, che recita: I = ICM + MD2, dove il significato dei vari termini dovete
saperlo voi!]
ICM = …………………………………… = ………… kg m2
m1rCM12+m2rCM2+m3rCM32=
2
2
2
2
m1((x1 –xCM) +(y1 –yCM) )+ m2((x2 –xCM) +(y2 –yCM) )+ m3((x3 –xCM)2+(y3 –yCM)2)= m1((x1 –0)2+(y1
+d/3)2)+ m2((x2 –0)2+(y2 +d/3)2)+ m3((x3 –0)2+(y3 +d/3)2)= (14/3) md2 = 0.25 Kg m2
[il risultato
si ottiene ovviamente sia applicando il teorema degli assi paralleli che calcolando direttamente il momento di inerzia
rispetto al polo passante per il CM; per il teorema, potete verificare il risultato prendendo notando che deve, per esempio,
essere: ICM = I0 – 3m(xCM2+yCM2) , dato che la distanza tra il polo a cui è riferito I0 (l’origine) e il CM vale D =
(xCM2+yCM2)1/2 e la massa totale è M = 3m]
e. Supponete ora che sui tre corpi agiscano rispettivamente le forze (costanti) F1 = (-f,0), F2 = (f, f),
F3 = (f,0), con f = 1.8 N. Cosa potete dire del moto del sistema? Quanto valgono l’accelerazione
del centro di massa, aCM , e l’accelerazione angolare α per rotazioni attorno al centro di massa?
Commento: ............................................ il sistema è sottoposto ad un moto di traslazione, dovuto
alla risultante delle forze che agiscono sul CM, e di rotazione, dovuto alla presenza di momenti
delle forze.
(F1+F2+F3)/(3m) = (f, f)/(3m) = (1.0, 1.0) m/s2
[il
aCM = (……, ……) = ………… m/s2
CM si muove di moto uniformemente accelerato e traiettoria rettilinea diretta lungo la bisettrice del primo quadrante]
α = …………………………………… ~ ………… rad/s2
(|τ1+ τ2+τ3|)/ICM = -|τ2|/ICM = - 2
2
df/(3ICM) = - f/(7md) ~ - 1.4 rad/s [dalla legge cardinale del moto rotatorio attorno al CM: τ = ICM α, dove τ indica la
risultante dei momenti delle forze, che è pari al solo momento τ2 dato che i momenti delle forze sulle masse 1 e 3 si annullano a
vicenda per ragioni di simmetria; notate che il segno negativo è stato aggiunto ad hoc per indicare che l’accelerazione tende a far
ruotare il sistema in senso orario. Per il calcolo di τ2 potete usare la regola del prodotto vettoriale τ2 = r2CM X F2, stando attenti a
scrivere nel modo corretto il vettore posizione della massa 2 rispetto al centro di rotazione, r2CM = r2 + rCM, e calcolando il prodotto
vettoriale ad esempio tramite la “regola del determinante”, consigliata quando si conoscono le componenti dei vettori da
“moltiplicare” fra loro; notate che l’evoluzione temporale di questo moto non è facilmente deducibile, poichè il momento cambia
con il tempo anche se siete in presenza di forze costanti]
3. Un’asta di massa M = 10.0 kg, lunghezza L = 3.00 m e sezione di area A = 10.0 cm2, è realizzata con
un materiale disomogeneo.
a. Sapendo che, detta x la distanza da un estremo dell’asta, la densità di massa varia in funzione di x
secondo la legge ρ(x) = ρ0 x2/L2, quanto vale il coefficiente ρ0?
ρ0 = …………………………………… = ………… kg/m3
ML2/(S ∫0Lx2dx) = 3M/(SL) =
4
3
1.00x10 kg/m [per definizione di densità di massa, deve essere M = ∫VOL ρ(x) dV = ∫0L ρ(x) Sdx =∫0L ρ0x2 (S/L2) dx
= ρ0( S/L2) ∫0L x2 dx = ρ0 SL /3 , dove l’elemento di volume è stato scritto come dV = Sdx coerentemente con la geometria
lineare del sistema]
b. A quale distanza xCM misurata rispetto all’estremo x = 0 dell’asta si trova il suo centro di massa?
xCM = …………………………………… = ………… m (∫0Lx ρ(x) S dx)/M = ρ0 S L2/(4M) =
(3M/(SL))( S L2/(4M) ) = 3L/4 = 2.25 m
c. Supponete ora che questa asta possa ruotare senza attrito su un piano
verticale e attorno ad un perno passante per il suo estremo x = 0.
θ
g
Supponete anche che all’altro estremo dell’asta sia attaccata una molla, di
M,
massa trascurabile e costante elastica k = 30.0 N/m e che l’altro estremo
L,
della molla sia vincolato ad un solaio rigido ed indeformabile. La figura
k, Δ
A
rappresenta la situazione di equilibrio, che si verifica quando la molla è
Y
ξ
diretta ortogonalmente all’asta, mentre l’asta forma un angolo θ = 60
X
gradi rispetto all’orizzontale. Quanto vale l’allungamento Δ della molla in
2
queste condizioni? [Usate il valore numerico g = 9.80 m/s per il modulo
dell’accelerazione di gravità]
Δ = …………………………………… = ………… m
Mg xCMcosθ / (kL) = 3Mg cosθ / (4k) =
2.45 m
[viene dall’equilibrio dei momenti delle forze rispetto al perno di rotazione, notando che le forze che danno
un momento non nullo sono la forza peso Mg, applicata al baricentro e quindi con un braccio xCMcosθ rispetto al perno, e
la forza elastica, di modulo kΔ e braccio L , essendo diretta ortogonalmente all’asta]
Francesco Fuso – tel 050 2214305 – e-mail: [email protected] – web page: http://www.df.unipi.it/~fuso/dida