Laurea in Statistica e Informatica per la Gestione delle Imprese
Università degli Studi di Perugia
STATISTICA AZIENDALE II (SERIE STORICHE) – A. A. 2003/2004
Marco Minozzo
4. Funzione di autocorrelazione e funzione di autocorrelazione parziale
Esercizio A. Si consideri il processo media mobile
a t ≈ WN (0, σ ) , σ = 1 / 3 , ( t =
2
a
2
a
,−2,−1,0,1,2,
Yt = (1 / 4)(at + at −1 + a t − 2 + at −3 ) , con
).
a) Si verifichi la stazionarietà, in senso debole, del processo Yt .
b) Calcolare e disegnare la funzione di autocorrelazione (globale) ρ (k ) .
c) Calcolare e disegnare la funzione di autocorrelazione parziale π (k ) , k = 0,1,2,3 .
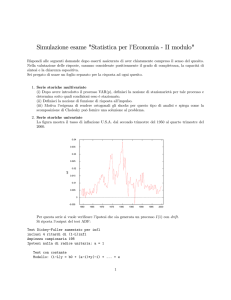
Esercizio B. Si consideri la serie storica y t dei quozienti di nuzialità in Italia dal 1863 al 1984. (La serie
è disponibile in formato Excel all’indirizzo http://www.stat.unipg.it/EDUCATION/moodle nel file
Nuzialità.xls.)
a) Rappresentare graficamente la serie storica.
b) Rappresentare graficamente con un diagramma a dispersione le coppie di punti (y t −1 , y t ) , (y t −5 , y t ) e
(y t −10 , y t ) ed interpolare con la retta dei minimi quadrati y t verso y t −1 , y t −5 e y t −10 rispettivamente.
c) Si calcoli e si disegni il correlogramma per k = 0,1, ,30 , illustrando il significato dei risultati
ottenuti.
d) Facendo uso degli intervalli di confidenza approssimati di Bartlett, si verifichi l’ipotesi che la serie
storica in questione provenga da un processo incorrelato (white noise).
e) Si calcoli e si disegni il correlogramma parziale per k = 0,1,2,3,4 .