Teoria delle perturbazioni indipendenti dal
tempo
Sia data Ĥ0 e si assuma di avere risolto in modo esatto il
problema agli autovalori:
!
Ĥ0Ψn0=En0Ψn0; <Ψn0│Ψm0>=δn,m
!
N.B. Non succede quasi mai per i sistemi veramente interessanti.
Es: atomi. Siamo capaci di trovare gli autostati per il solo
idrogeno, sempre che non si voglia considerare la “struttura fine”.
E’ allora essenziale essere almeno in grado di trovare i livelli
energetici (e le autofunzioni) di sistemi interessanti in modo
approssimato.
Sia data Ĥ0 e si assuma di avere risolto in modo esatto il
problema agli autovalori:
!
Ĥ0Ψn0=En0Ψn0; <Ψn0│Ψm0>=δn,m
!
Ora consideriamo lo stesso sistema, ma soggetto a una
debole perturbazione, per cui Ĥ=Ĥ0+Ĥ’. L’equazione agli
autovalori si scriverà
!
ĤΨn=EnΨn=(Ĥ0+Ĥ’)Ψn
!
e in generale non ammetterà risoluzione analitica esatta.
ĤΨn=EnΨn=(Ĥ0+Ĥ’)Ψn
!
in generale non ammetterà risoluzione analitica esatta.
!
Due strade:
a) la risolvo numericamente con l’ausilio di un
computer
b) cerco un metodo per risolverla analiticamente, ma in
modo approssimato.
!
In questo corso seguiremo la strada b).
ĤΨn=EnΨn=(Ĥ0+Ĥ’)Ψn
Cosa vuol dire che Ĥ’ è una “debole perturbazione”?
Classicamente l’interpretazione è immediata: significa che
l’aggiunta del nuovo termine energetico cambia di poco
l’energia del sistema.
!
!
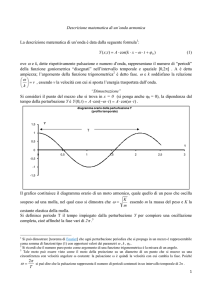
Energia potenziale: V0(x)
Energia potenziale: V0(x)+H’(x)
ĤΨn=EnΨn=(Ĥ0+Ĥ’)Ψn
Cosa vuol dire che Ĥ’ è una “debole perturbazione”?
Dal punto di vista della meccanica quantistica significa che
i valori di aspettazione <Ĥ’> dovranno essere piccoli rispetto ai
corrispondenti <Ĥ0>, e così ogni elemento di matrice
(Nella pratica, ciò è garantito dal confronto tra le energie
classiche e imperturbate).
N.B.
in linea di principio uno può sempre provare ad applicare la
teoria che segue, se i “nuovi” autovalori sono molto diversi
da quelli imperturbati, allora deve sospettare che
l’approssimazione non sia buona.
ĤΨn=EnΨn=(Ĥ0+Ĥ’)Ψn
Ok, se la perturbazione è debole, posso sempre pensare di scrivere
(classicamente) H’=λH’’ , dove λ<<1, e (H’’=H’/λ)
è confrontabile con H0. In meccanica quantistica, Ĥ’=λĤ’’.
Ĥ=Ĥ0+Ĥ’=Ĥ0+λĤ’’; λ<<1.
A
B
λ
H’=f(x)=(A/B)(B/A)f(x)
H’’
Ĥ0Ψn0=En0Ψn0
En0 e Ψn0 NOTI
ĤΨn=EnΨn=(Ĥ0+λĤ’’)Ψn; λ<<1.
En e Ψn DA STIMARE
Idea: provo a espandere sia En sia Ψn in potenze di λ, di modo
che per λ->0 tendano al valore imperturbato:
En=En0 +λEn(1) +λ2En(2)+…
(E)
Ψn=Ψn0 +λΨn(1) +λ2Ψn(2)+…
(Ψ)
(Ĥ0+λĤ’’)(Ψn0 +λΨn(1) +λ2Ψn(2)+…)=
(En0 +λEn(1) +λ2En(2)+…)(Ψn0 +λΨn1(1) +λ2Ψn(2)+…)
(Ĥ0+λĤ’’)(Ψn0 +λΨn(1) +λ2Ψn(2)+…)=
(En0 +λEn(1) +λ2En(2)+…)(Ψn0 +λΨn1(1) +λ2Ψn(2)+…)
(Ĥ0+λĤ’’)(Ψn0 +λΨn(1) +λ2Ψn(2)+…)=
(En0 +λEn(1) +λ2En(2)+…)(Ψn0 +λΨn(1) +λ2Ψn(2)+…)
Raccolgo in ambo i membri i termini con uguale dipendenza da λ
Ĥ0Ψn0+λ(Ĥ0Ψn(1)+Ĥ’’Ψn0)+λ2(Ĥ0Ψn(2)+Ĥ’’Ψn(1))+…
=En0Ψn0+λ(En0Ψn(1)+En(1)Ψn0)+λ2(En0Ψn(2)+En(1)Ψn(1)+En(2)Ψn0)
Uguagliando i termini di eguali potenze (immaginare di portare
tutto a primo membro e di uguagliare a zero …)
Ĥ0Ψn0+λ(Ĥ0Ψn(1)+Ĥ’’Ψn0)+λ2(Ĥ0Ψn(2)+Ĥ’’Ψn(1))+…
=En0Ψn0+λ(En0Ψn(1)+En(1)Ψn0)+λ2(En0Ψn(2)+En(1)Ψn(1)+En(2)Ψn0)
Uguagliando i termini di eguali potenze (immaginare di portare
tutto a primo membro e di uguagliare a zero …)
Ĥ0Ψn0=En0Ψn0 ordine zero in λ
Ĥ0Ψn(1)+Ĥ’’Ψn0=En0Ψn(1)+En(1)Ψn0 ordine uno in λ
Ĥ0Ψn(2)+Ĥ’’Ψn(1)=En0Ψn(2)+En(1)Ψn(1)+En(2)Ψn0
ordine due in λ
Ĥ0Ψn(1)+Ĥ’’Ψn0=En0Ψn(1)+En(1)Ψn0 ordine uno in λ
Ĥ0Ψn(1)+Ĥ’’Ψn0=En0Ψn(1)+En(1)Ψn0 ordine uno in λ
Ĥ0│Ψn(1)>+Ĥ’’│Ψn0>=En0│Ψn(1)>+En(1)│Ψn0>
<Ψn0│Ĥ0│Ψn(1)>+<Ψn0│Ĥ’’│Ψn0>=<Ψn0│En0│Ψn(1)>+<Ψn0│En(1)│Ψn0>
hermitiana!
En(1)
En0<Ψn0│Ψn(1)>+<Ψn0│Ĥ’│Ψn0>= En0<Ψn0│Ψn(1)>+En(1)
En(1)=<Ψn0│Ĥ’│Ψn0>
Al prim’ordine (in λ), se
Ĥ=Ĥ0+Ĥ’
En=En0+λ<Ψn0│Ĥ’’│Ψn0>
En=En0+<Ψn0│Ĥ’│Ψn0>
Risultato fondamentale: la correzione al prim’ordine apportata
da una perturbazione a un livello energetico è
data dal VALORE MEDIO DELLA PERTURBAZIONE calcolato sul
corrispondente stato imperturbato.
Correzione al I ordine della funzione d’onda
Ĥ0Ψn(1)+Ĥ’’Ψn0=En0Ψn(1)+En(1)Ψn0
(Ĥ0-En0)Ψn(1)=-(Ĥ’’-En(1))Ψn0
Sviluppo Ψn(1) sul sonc Ψn0: Ψn(1)=∑m cm,nΨm0
Correzione al I ordine della funzione d’onda
Ĥ0Ψn(1)+Ĥ’’Ψn0=En0Ψn(1)+En(1)Ψn0
(Ĥ0-En0)Ψn(1)=-(Ĥ’’-En(1))Ψn0
Sviluppo Ψn(1) sul sonc Ψn0: Ψn(1)=∑m cm,nΨm0
Oss: se Ψn(1) soddisfa (Ĥ0-En0)Ψn(1)=-(Ĥ’’-En(1))Ψn0
lo stesso vale per ogni funzione Ψn(1)+αΨn(0),
quindi la Ψn(1) è determinata a meno di una
costante libera α. Scelgo allora α=-cn,n di modo
che Ψn(1)=∑m≠n cm,nΨm0
Ciò equivale ad imporre la normalizzazione della
funzione d’onda approssimata al prim’ordine:
Ψn=Ψn0 +λΨn(1) ;
<Ψn│Ψn>=<Ψn0│Ψn0>+λ(<Ψn0│Ψn1>+<Ψn0│Ψn1>);
!
<Ψn│Ψn>=1+λ(<Ψn0│Ψn1>+<Ψn0│Ψn1>);
!
<Ψn0│Ψn(1)>=<Ψn0│∑m≠n cm,nΨm0>=∑m≠n cm,n <Ψn0│Ψm0>=0
Ok, quindi riparto da:
(Ĥ0-En0)Ψn(1)=-(Ĥ’’-En(1))Ψn0
E inserisco lo sviluppo:
Ψn(1)=∑m≠n cm,nΨm0
(Ĥ0-En0)Ψn(1)=-(Ĥ’’-En(1))Ψn0
Ψn(1)=∑m≠n cm,nΨm0
(Ĥ0-En0)∑m≠n cm,n│Ψm0>=-(Ĥ’’-En(1))│Ψn0>;
∑m≠n cm,n(Em0-En0)│Ψm0>=-(Ĥ’’-En(1))│Ψn0>; Ora
∑m≠n cm,n(Em0-En0)
applico <Ψl0│
<Ψl0│Ψm0>=-<Ψl0│Ĥ’’│Ψn0>+En(1)δl,n;
∑m≠n cm,n(Em0-En0)δl,m
=-<Ψl0│Ĥ’’│Ψn0>+En(1)δl,n;
∑m≠n cm,n(Em0-En0)δl,m
=-<Ψl0│Ĥ’’│Ψn0>+En(1)δl,n;
Se l=n ottengo <Ψn0│Ĥ’’│Ψn0>=En(1) che è la correzione
all’energia al I ordine che avevamo già ottenuto. Se invece
l≠n, allora ottengo una stima della “correzione”
al I ordine da apportare alla funzione d’onda per tenere
conto della perturbazione. Ottengo infatti:
cl,n(El0-En0)=-<Ψl0│Ĥ’’│Ψn0>;
cl,n=<Ψl0│Ĥ’’│Ψn0>/(En0-El0); l≠n e quindi:
Ψn(1)=∑m≠n cm,nΨm0=∑l≠n cl,nΨl0 ->
Ψn(1)=∑l≠n [<Ψl0│Ĥ’’│Ψn0>/(En0-El0)]Ψl0;
λΨn(1)=∑l≠n [<Ψl0│Ĥ’│Ψn0>/(En0-El0)]Ψl0;
Riassumendo, in presenza di una piccola perturbazione Ĥ’ ad
un hamiltoniana Ĥ0, possiamo calcolare al I ordine i livelli
energetici e le funzioni d’onda nel seguente modo:
En=En0+<Ψn0│Ĥ’│Ψn0>
Ψn=Ψn0+
∑
l≠n
<Ψl0│Ĥ’│Ψn0>
(En0-El0)
│Ψl0>
Notare che per calcolare la correzione all’energia uso solo
gli elementi di matrice diagonali della perturbazione.
En=En0+<Ψn0│Ĥ’│Ψn0>+…
Al contrario, per correggere la funzione d’onda servono quelli
non diagonali.
Ψn=Ψn0+
∑
l≠n
<Ψl0│Ĥ’│Ψn0>
(En0-El0)
Ψl0
In presenza di una perturbazione la funzione d’onda relativa a
un certo livello “riceve contributi” anche dalle funzioni d’onda
di livelli imperturbati diversi. Più sono vicini in energia e più
contribuiscono.
Correzione ai livelli energetici: second’ordine.
Ĥ0Ψn(2)+Ĥ’’Ψn(1)=En0Ψn(2)+En(1)Ψn(1)+En(2)Ψn0 ordine due in λ (**)
Ψn(1)=
∑
l≠n
<Ψl0│Ĥ’’│Ψn0>
(En0-El0)
│Ψl0>
Correzione ai livelli energetici: second’ordine.
Ricordo il risultato:
Ĥ0Ψn0=En0Ψn0 ordine zero in λ
Ĥ0Ψn(1)+Ĥ’’Ψn0=En0Ψn(1)+En(1)Ψn0 ordine uno in λ (*)
Ĥ0Ψn(2)+Ĥ’’Ψn(1)=En0Ψn(2)+En(1)Ψn(1)+En(2)Ψn0 ordine due in λ (**)
Per ottenere l’ordine 1 avevamo sfruttato la (*), ora
sfruttiamo la (**)
Ĥ0│Ψn(2)>+Ĥ’’│Ψn(1)>=En0│Ψn(2)>+En(1)│Ψn(1)>+En(2)│Ψn0>
Ĥ0│Ψn(2)>+Ĥ’’│Ψn(1)>=En0│Ψn(2)>+En(1)│Ψn(1)>+En(2)│Ψn0>
Applico <Ψn0│:
<Ψn0│Ĥ0│Ψn(2)>+ <Ψn0│Ĥ’’│Ψn(1)>
=En0<Ψn0││Ψn(2)>+En(1)<Ψn0│Ψn(1)>+En(2)
En0<Ψn0│Ψn(2)>+ <Ψn0│Ĥ’’│Ψn(1)>
=En0<Ψn0││Ψn(2)>+En(1)<Ψn0│Ψn(1)>+En(2)
En(2)= <Ψn0│Ĥ’’│Ψn(1)>-En(1)<Ψn0│Ψn(1)>
En(2)= <Ψn0│Ĥ’’│Ψn(1)>-En(1)<Ψn0│Ψn(1)>. Ma
Ψn(1)=
∑
<Ψl0│Ĥ’│Ψn0>
(En0-El0)
l≠n
<Ψn0│Ψn(1)>=
∑
(En0-El0)
<Ψn0│Ĥ’’│Ψn(1)>=
En(2)=(1/λ2)
∑
da cui:
<Ψl0│Ĥ’│Ψn0>
l≠n
En(2)=
Ψl0
∑
<Ψn0│Ψl0>=0
<Ψl0│Ĥ’│Ψn0>
l≠n
(En0-El0)
|<Ψl0│Ĥ’│Ψn0>|2
l≠n
(En0-El0)
(1/λ2)<Ψn0│Ĥ’│Ψl0>
Data Ĥ=Ĥ0+Ĥ’ con H’(classica) “piccola”,
ovvero H’=λH’’; λ=numero puro <<1, H’’=H’/λ
confrontabile con H0, allora …
En=En0+<Ψn0│Ĥ’│Ψn0>+
∑
|<Ψl0│Ĥ’│Ψn0>|2
l≠n
(En0-El0)
+ …
Per la funzione d’onda ci accontentiamo dello
sviluppo al I ordine:
Ψn=Ψn0+
∑
l≠n
<Ψl0│Ĥ’│Ψn0>
(En0-El0)
Ψl0
Attenzione! Risultati validi solo se il livello
n è non degenere!!!
Abbiamo indicato i livelli energetici con un unico indice n,
“riassuntivo” del set completo di numeri quantici. (Ad esempio
n->n,l,m,ms). Così facendo però ci siamo persi la possibilità di
avere degenerazione (ce ne saremmo accorti se avessimo usato
n,l,m,mS e En). Nel formalismo semplificato, avere degenerazione
significa considerare la possibilità che En=El per qualche l≠n.
In questo caso le espressioni qui sotto divergono!!!!
En=En0+<Ψn0│Ĥ’│Ψn0>+
Ψn=Ψn0+
∑
l≠n
∑
<Ψl0│Ĥ’│Ψn0>
(En0-El0)
|<Ψl0│Ĥ’│Ψn0>|2
Ψl0
(En0-El0)
+ …
Dove sta il problema?
Supponiamo di avere un sistema in cui l’energia dipenda da
tutti i numeri quantici n,l,m,ms, per cui non ho degenerazione.
Il punto di partenza della teoria perturbativa era:
En,l,m,ms=En,l,m,ms0 +λEn,l,m,ms(1) +λ2En,l,m,ms(2)+…
(E)
Ψn,l,m,ms=Ψn,l,m,ms0 +λΨn,l,m,ms(1) +λ2Ψn,l,m,ms(2)+…
(Ψ)
En,l,m,ms
λ
Qui suppongo che la perturbazione alzi il livello energetico. Se
lo abbassa il discorso non cambia.
Dove sta il problema?
Supponiamo di avere un sistema in cui l’energia dipenda da
tutti i numeri quantici n,l,m,ms, per cui non ho degenerazione.
Il punto di partenza della teoria perturbativa era:
En,l,m,ms=En,l,m,ms0 +λEn,l,m,ms(1) +λ2En,l,m,ms(2)+…
(E)
Ψn,l,m,ms=Ψn,l,m,ms0 +λΨn,l,m,ms(1) +λ2Ψn,l,m,ms(2)+…
(Ψ)
Se parto da una certa
intensità di perturbazione e
la porto a zero, finisco con
En,l,m,ms0
continuità su En,l,m,ms0
cui corrisponde Ψn,l,m,ms0
λ
Qui suppongo che la perturbazione alzi il livello energetico. Se
lo abbassa il discorso non cambia.
Adesso suppongo che m sia un indice di degenerazione
En,l,ms=En,l,ms0 +λEn,l,ms(1) +λ2En,l,ms(2)+…
Opportune perturbazioni possono rompere tale degenerazione
En,l,m=1,ms
En,l,ms0
En,l,m=0,ms
En,l,m=-1,ms
λ
QUALUNQUE combinazione lineare ∑mcmΨn,l,m,ms0 corrisponde a questa energia.
Ma c’è una SPECIFICA combinazione lineare associata ad ogni ramo della
curva.
Teoria perturbativa (statica) per livelli degeneri. Consideriamo
per semplicità un livello energetico E0 con degenerazione 2, per
cui esistono due funzioni d’onda tali per cui:
!
Ĥ0Ψa0= E0;
Ĥ0Ψb0= E0.
<Ψa0│Ψb0 >=0
Ovviamente, qualunque combinazione lineare del tipo
Ψ0=αΨa0+βΨb0 verificherà: Ĥ0Ψ0= E0.
Adesso consideriamo
Ĥ=Ĥ0+Ĥ’=Ĥ0+λĤ’’ ed imponiamo le solite espansioni:
E=E0 +λE(1) +λ2E(2)+…
(E)
Ψ=Ψ0 +λΨ(1)+λ2Ψ(2)+…
(Ψ)
con Ψ0=αΨa0+βΨb0
Adesso consideriamo
Ĥ=Ĥ0+Ĥ’=Ĥ0+λĤ’’ ed imponiamo le solite espansioni:
E=E0 +λE(1) +λ2E(2)+…
(E)
Ψ=Ψ0 +λΨ(1)+λ2Ψ(2)+…
(Ψ)
con Ψ0=αΨa0+βΨb0
Esattamente come nel caso non degenere, sostuituendo in
ĤΨ=EΨ e raccogliendo i termini di eguale potenza in λ trovo:
Ĥ0Ψ0=E0Ψ0
ordine zero in λ
Ĥ0│Ψ(1)>+Ĥ’’│Ψ0>=E0│Ψ(1)>+E(1)│Ψ0> ordine uno in λ
Semplifichiamo la notazione e uniformiamola a quella
del Griffith. Il passaggio H’=λH’’=λ(H’/λ) serviva a
chiarire il significato delle espansioni. Ma abbiamo visto
che, una volta individuati i termini di ugual potenza in
λ, i risultati finali non dipendevano da λ(prima dividevo,
poi moltiplicavo per λ); l’importante è che H’ sia piccolo.
Di fatto, posso ragionare per λ=1, per cui H’=H’’
applico <Ψa0│
<Ψa0│ Ĥ0│Ψ(1)>+ <Ψa0│ Ĥ’│Ψ0>=E0 <Ψa0│Ψ(1)>+E(1) <Ψa0│Ψ0>
E0<Ψa0│Ψ(1)>+ <Ψa0│ Ĥ’│Ψ0>=E0 <Ψa0│Ψ(1)>+E(1) <Ψa0│Ψ0>
<Ψa0│ Ĥ’│Ψ0>=E(1) <Ψa0│Ψ0>
<Ψa0│ Ĥ’│Ψ0>=E(1) <Ψa0│Ψ0>
con Ψ0=αΨa0+βΨb0
<Ψa0│ Ĥ’│αΨa0+βΨb0>=E(1) <Ψa0│αΨa0+βΨb0>
α<Ψa0│ Ĥ’│Ψa0>+β<Ψa0│ Ĥ’’│Ψb0>=αE(1)
αWaa+βWab=αE(1)(*)
Wij=<Ψi0│ Ĥ’│Ψj0>; (i,j)=a,b
Se invece avessi applicato <Ψb0│ avrei trovato:
αWba+βWbb=βE(1)(**)
La (*) e la (**) possono essere combinate nell’unica equazione
matriciale:
(
Waa Wab
Wba Wbb
)( )
α
β
=E(1)
( )
α
β
con Ψ0=αΨa0+βΨb0
αWaa+βWab=αE(1)(*)
Wij=<Ψi0│ Ĥ’’│Ψj0>; (i,j)=a,b
αWba+βWbb=βE(1)(**)
(
Waa Wab
Wba Wbb
)( )
α
β
=E(1)
( )
α
β
E’ un’equazione agli autovalori per la matrice W. Gli autovettori
forniscono i coefficienti delle combinazioni lineari “corrette”, gli
autovalori i possibili valori di energia al I ordine.
Per trovarli impongo che det(W-E(1)I)=0….
(Waa-E(1))(Wbb-E(1))=WabWba;
!
WaaWbb+[E(1)]2-E(1)Wbb-E(1)Waa=WabWba
WaaWbb+[E(1)]2-E(1)Wbb-E(1)Waa=WabWba;
!
[E(1)]2-E(1)(Wbb+Waa)+(WaaWbb-WabWba)=0
E(1)= (1/2)
[Wbb+Waa±
Wbb2+Waa2+2WbbWaa-4WaaWbb+4WabWba
E(1)= (1/2)
[Wbb+Waa±
Wbb2+Waa2-2WbbWaa+4WabWba
E(1)±= (1/2)
[Wbb+Waa±
(Waa2-Wbb2)+4│WabWba│2
]
]
]
Ma Wab=Wba*➞
E(1)±= (1/2)
[Wbb+Waa±
(Waa2-Wbb2)+4│WabWba│2
]
E(1)+
E0
E(1)-
λ
Se λ➞0+ lungo qualunque curva, finisco sempre in E0. MA, la
funzione d’onda corrispondente è del tipo Ψ0=αΨa0+βΨb0 con
(α,β)=(α-,β-)=autovettore corrispondente a E(1)- se mi muovo lungo
quella inferiore, (α,β)=(α+,β+) autovettore corrispondente
a E(1)+ se mi muovo lungo quella superiore.
Generalizzazione a degenerazione qualunque
N.B. La perturbazione potrebbe
E0
rompere la degenerazione solo
parzialmente. Ciò avviene se qualche
autovalore di W è degenere.
λ
ĤΨi0=E0Ψi0; i=1,…,m indice di degenerazione
Ψ0=∑αiΨi0
Al I ordine l’energia è data dagli autovalori
della matrice mXm W; Wij= <Ψi0│Ĥ’│Ψj0>
Ancora degenerazione 2,
ma se è “m” è identico
con Ψ0=αΨa0+βΨb0
αWaa+βWab=αE(1)(*)
Wij=<Ψi0│Ĥ’│Ψj0>; (i,j)=a,b
αWba+βWbb=βE(1)(**)
(
Waa Wab
Wba Wbb
)( )
α
β
=E(1)
( )
α
β
E se W fosse stata direttamente diagonale?
(
Waa 0
0 Wbb
)
Gli autovalori sarebbero stati semplicemente Waa e Wbb.
( ) ( )
0
1
e gli autovettori:
1
0
Quindi le “combinazioni lineari” sono semplicemente
Ψa0 e Ψb0
NOTARE CHE Waa e Wbb altro non sono che l’espressione
della correzione al I ordine nella teoria perturbativa
(semplice) per livelli non degeneri.
Diagonalizzare W è noioso. Ma in molti casi posso evitarlo. Infatti,
consideriamo ad esempio l’atomo di idrogeno (o un atomo
idrogenoide):
En0;Ψn,l,m,ms0
Ĥ0
L2
Lz
Sz
Fisso ad esempio n=1, e quindi l=0,m=0,ms=±1/2; 2 volte degenere
in ms. Se ho una perturbazione devo tenerne conto. Ma se
la perturbazione commuta con Sz, allora avrà autofunzioni
comuni ad esso, per cui <Ψms0│ Ĥ’│Ψms’0>=0, W è diagonale.
Posso allora applicare la teoria delle perturbazioni per stati non
degeneri partendo dall’autofunzione relativa a ms=+1/2 e
da quella relativa a ms=-1/2.
Diagonalizzare W è noioso. Ma in molti casi posso evitarlo. Infatti,
consideriamo ad esempio l’atomo di idrogeno (o un atomo
idrogenoide):
En0;Ψn,l,m,ms0
Ĥ0
L2
Lz
Sz
Più in generale, se la perturbazione commuta con uno degli
operatori che determinano i numeri quantici dell’hamiltoniana
imperturbata, ho speranze di evitare la teoria delle perturbazioni
per livelli degeneri.