Problemi teorici sull`Alternatore - Digilander

PROBLEMI DI FEM CINETICA – alternatore
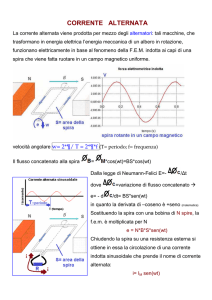
Considera l’Alternatore disegnato in figura: è composto da una singola spira di lato quadrato L=30cm che
ruota con velocità angolare 0=13rad/s in senso antiorario rispetto a te, investita da un campo magnetico
B0=0,5T. Considera che la spira possiede una resistenza R=20.
Riguardo alle domande: tieni conto che, a differenza del caso lineare, per un Alternatore la tensione e la
corrente è –non a caso- di valore alternato fra un max ed un min: perciò non potrò chiedere “qual è il valore
della tensione e qual è il valore della corrente” perché essi non sono costanti: posso però chiedere “qual è la
funzione che permette di calcolare la tensione e la corrente al passare del tempo”.
1) Calcola l’Area della spira.
2) Scrivi l’equazione del flusso magnetico (B) in funzione del tempo, supponendo che l’angolo =0°
quando t=0s. Specifica qual è il verso “+” del flusso.
3) Calcola l’equazione della fem indotta ().
4) Calcola l’equazione della corrente indotta (I).
5) Calcola la potenza elettrica istantanea indotta.
6) Calcola il valore della forza magnetica applicata da B0 sui lati della spira (Fm). Fm accelera o
rallenta la rotazione della spira?
7) Calcola il braccio di Fm ed il momento  di Fm.
8) Calcola il valore della potenza istantanea prodotta da .
9) E’ un caso che la potenza di  sia uguale ed opposta a quella elettrica?
Un attimo di relax e poi ripartiamo…
10) Qual è la potenza elettrica media in un periodo? Qual è il Lavoro elettrico complessivo fornito in
200 s?
11) Calcola il valore efficace EFF e IEFF.
Infine, qualche domanda che sicuramente vi sarà fatta all’orale:
12) Qual è il periodo dell’Alternatore? Qual è la sua frequenza?
13) [Questa è una domanda di trigonometria: rispondete, così vi fate un ripasso di Matematica] Per
quali istanti di tempo  , I e la potenza istantanea sono nulli? Per quali istanti essi sono minimi?
Per quali istanti essi sono massimi?
14) Qual è il Lavoro prodotto dall’Alternatore in un periodo?
15) IMPORTANTE! Come cambiano le risposte se invece di 1 spira l’Alternatore possiede 100 spire?
Adesso pensa un attimo e rispondi a queste domande :
a) Quale dei punti soprastanti ci fa capire che il circuito non ha poli elettrici?
b) Quali dei punti soprastanti ci fa capire che il campo elettrico indotto (Ein) non è conservativo?
c) Quali dei punti sovrastanti ci fa capire che il campo elettrico indotto fornisce energia al circuito?
d) Quale dei punti sovrastanti ci fa capire che si ha trasduzione di energia da cinetica ad elettrica?
e) In quale dei punti sovrastanti è evidente l’effetto della legge di Lenz?
f) Cosa accadrebbe se la legge di Lenz non valesse (cioè: se l’equazione della fem indotta fosse
=+
𝐷
)?
𝐷𝑡
g) Perché si introducono i valori efficaci EFF e IEFF?
Risposte
1) [Area=900cm2=0,09m2]
2) [(B) = AreaB0cos() ; =0t  (B) = 0,090,5cos(13t) = 0,045cos(13t) Weber ; il verso
“+” è quello antiorario se visto dal magnete Nord]
𝐷
𝐷𝑡
3) [=- -
= 0,04513sen(13t) = 0,585sen(13t) Volt ; il coefficiente del seno -cioè il valore
0,585- è il massimo valore raggiungibile da  e perciò in classe lo abbiamo indicato con M (VF)
o MAX (VB). Perciò posso anche scrivere: =Msen(13t)]
4) [I = /R = 0,02925sen(13t) A ; il coefficiente del seno -cioè il valore 0,02925- è il massimo
valore raggiungibile da  e perciò in classe lo abbiamo indicato con M (VF) o IMAX (VB). Perciò
posso anche scrivere: =Msen(13t)]
5) [Pot = I = 2/R = I2R = 0,01711125sen(13t)2 W]
6) [Fm = BIL = 0,0043875sen(13t) N ; il verso di Fm è verso l’alto per il lato superiore e verso il
basso per il lato inferiore  Fm rallenta la sbarra.]
7) [Braccio di Fm = L/2sen()2 (moltiplico tutto per 2 perché ho due forze: una applicata al lato
superiore e l’altra a quello inferiore, come abbondantemente spiegato a lezione)  braccio =
0,3sen(13t) ;  = Fmbraccio = 0,00131625 Nm .
8) [Pot istantanea di  =  = -0,01711125sen(13t)2 –perché il segno “-“? Pensaci…-]
9) [No]
__________________________________________________________________________
10) [Potenza media 1 periodo = M2/R½
= 0,008555625 W ; Lavoro = Potenzat =
0,008555625W200s = 1,711125J –posso usare la formula della potenza costante perché sto
usando la potenza media di 1 periodo, che è uguale per ogni periodo-.]
11) EFF = EM/2 = 0,414 V ; IEFF = IM/2 = 0,0207 A]
12) Sappiamo che il periodo (T) è legato alla velocità angolare dalla relazione: 0 = 2/T 
T=2/0 = 2/13 = 0,4833s. f= 1/T=2,069 Hz.
13) =0 quando l’argomento del seno è =0° o =  0t=0  t1=0s (1° soluzione) ; 0t= 
t2 = /0 = /13 = 0,24165s (2° soluzione). Nota che la 2° soluzione avviene esattamente a
metà periodo: infatti il seno si annulla all’inizio del periodo (=0° , prima soluzione) e a metà
periodo (=180° , seconda soluzione).
Alle due soluzioni bisogna aggiungere il termine periodico “nT, nN” perché la funzione seno si
ripete esattamente dopo ogni periodo: perciò scrivo: t1=n0,4833s , nN ; t2=0,24165s +
n0,4833s , nN. Per la corrente e la potenza i risultati sono gli stessi della fem.
Per quanto riguarda i valori massimi: il seno ha il massimo quando =/2  0t=/2  , I e
di conseguenza la Potenza istantanea hanno un massimo quando t=/(20) = 0,12083s ;
anche in questo caso bisogna aggiungere il termine periodico e perciò si ha: t = 0,12083 +
n0,4833s , nN.
Per quanto riguarda i valori minimi: il seno ha il minimo per =3/2  0t=3/2   , I
hanno il minimo per t=0,3625s + n0,4833s , nN. Per quanto riguarda la potenza istantanea:
quando  e I sono al minimo essa ha un massimo perché al minimo sia  che I sono negativi ma
la potenza è data dal loro prodotto “I” e perciò essa è positiva.
14) Stessa risposta del punto 10), soltanto che adesso come t uso il periodo T=0,4833s  Lavoro
= 0,008555625W0,4833s = 0,004135 J.
15) Il flusso e di conseguenza  , I devono essere moltiplicati per 100 ( ,  , I sono direttamente
proporzionali al numero delle spire). Le potenza istantanea e media devono essere moltiplicate
per 1002 poiché la potenza è data da 2/R e perciò è proporzionale al quadrato del numero delle
spire.
a)-f) Le risposte a) – f) sono identiche a quelle della fem cinetica lineare e perciò non le sto a
ripetere: segnate voi i punti associati.
g) Per quanto riguarda la risposta g): si introducono i valori efficaci perché la tensione (e di
conseguenza la corrente) di un alternatore viene raddrizzata, cioè resa costante usando
particolari strumenti elettrici che per mancanza di tempo non vi posso descrivere ma che sono
presenti in ogni impianto elettrico. Perciò dobbiamo porci la domanda: “Il nostro Alternatore che
ha una tensione alternata fra +0,585 V e -0,585 V quale tensione finale produce quando questa
viene resa costante?” La risposta è proprio il termine EFF=0,414 V, cioè: “il nostro alternatore
alla fine produce una tensione continua -cioè costante- di 0,414 V”. Stesso discorso per la
corrente.