Spettroscopia di risonanza Raman di
emoproteine
2
1
Cm
N
3
N
4
a
b
Fe
N
N
5
8
7
6
c
d
O
O
O
O
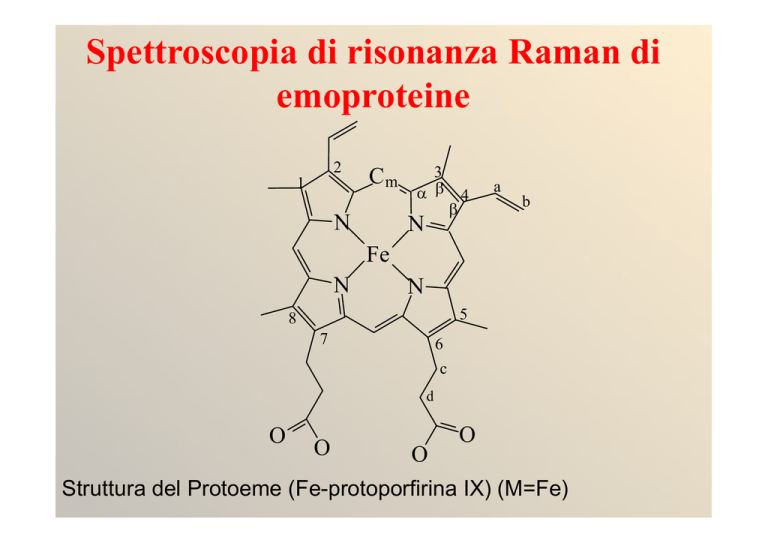
Struttura del Protoeme (Fe-protoporfirina IX) (M=Fe)
1)
Il sistema aromatico molto esteso
dell'anello porfirinico da' origine a due
transizioni elettroniche * nel visibile.
Banda Soret (o banda B).
403
Bande Q
505
534
649
Gli spettri Raman sono dominati dai modi vibrazionali della porfirina che possono
aumentare per risonanza.
Le transizioni elettroniche sono -*, polarizzate nel piano porfirinico, mentre le bande
Raman coinvolte si trovano nell’intervallo 1000-1700 cm -1 e si riferiscono allo
stretching nel piano dell’anello aromatico.
Le vibrazioni che coinvolgono l’atomo di Fe non sono particolarmente intensificate.
•
L'eccitazione in prossimità della banda Soret produce uno spettro dominato dai
modi totalsimmetrici A1g.
•
L'eccitazione in vicinanza delle bande Q produce scattering collegato alle
vibrazioni in grado di dare miscelamento fra le transizioni B e Q corrispondenti ai
modi non total-simmetrici di simmetria
Quindi gli spettri RR sono diversi !
Le frequenze vibrazionali sono sensibili a variazioni della
geometria della porfirina e della struttura elettronica.
Specifici modi vibrazionali sono molto sensibili alle
dimensioni del "core" della porfirina, allo stato di spin e
di ossidazione dell'atomo metallico centrale, e quindi
alla natura dei suoi leganti.
Spettro RR nella regione di alta
frequenza:
La regione di alta frequenza tra 1300-1700 cm-1 è
caratterizzata da vibrazioni di stiramento dei
legami dell’anello che danno orgine a bande
intense.
Sono chiamate bande marker delle dimensioni
del core, in quanto sono sensibili alle
dimensioni dell’anello: 0.01 Å di variazione
delle dimensioni del core comportano variazioni
di frequenza di 5-6 cm-1
Tutti i modi dello scheletro porfirinico compresi nella regione tra
1450 e 1650 cm-1 dello spettro RR [eccezion fatta per i
modi vinilici (C=C) streching (1618-1635 cm-1)] danno
una correlazione lineare negativa rispetto alle dimensioni del
"core" porfirinico,
Le dimensioni sono definite dalla proiezione del legame Fe-N
sul piano formato dai quattro N pirrolici (distanza Ct-N, Ct =
centro della porfirina).
La pendenza delle rette e' proporzionale al contributo
dello stretching dei legami metinici per ciascun modo
normale:
la dipendenza delle frequenze dalle dimensioni del
"core" e' infatti il risultato di cambiamenti nelle
costanti di forza del ponte metinico che avvengono
quando la porfirina si espande o si contrae.
• Poiche' gli anelli pirrolici sono relativamente rigidi, i
cambiamenti nelle dimensioni del "core" sono
accompagnati da alterazioni nella lunghezza e
nell'angolo dei legami metinici.
• I fattori che determinano le dimensioni del core
porfirinico sono lo stato di spin, lo stato di
coordinazione e di ossidazione del Fe.
D
D
Fe
N
N
N
N
N
N
Fe
F
N
N
N
N
D
Fe
N
N
F
5-c alto spin
6-c alto spin
6-c basso spin
o
FeIII 2.02 A
o
FeIII 2.04 A
FeIII 1.99 A
o
FeII 2.06 A
FeII 2.00 A
o
FeII 2.04 A
o
o
Diagramma schematico delle Fe-porfirine alto e basso spin, con le
tipiche dimensioni del "core", indicate per i complessi del FeII e
FeIII, ottenute prendendo la distanza fra la proiezione del Fe sul
piano porfirinico e uno degli atomi di azoto pirrolici
(distanza Ct-N, Ct = centro della porfirina).
D e F indicano rispettivamente un legante debole e forte
Le dimensioni del "core" dipendono anche dal numero di
coordinazione del Fe.
Nei complessi 6-coordinati l'atomo di Fe si trova piu' o
meno nel piano dell'eme e la differenza tra alto e basso
spin e' dovuta all'occupazione nel complesso alto spin
degli orbitali z2 e x2-y2,
N
N
N
Fe
Fe
Nei complessi 5-coordinati il Fe e'
N
N
N
N
spostato verso il quinto legante:
questo spostamento induce una
LS
HS
contrazione della cavita' della
S=1/2
S=5/2
porfirina.
His
His
His
L'effetto e' particolarmente forte
per i complessi 5-coordinati alto
spin ( 5cHS), in cui le dimensioni
del core sono intermedie tra
quelle del 6-coordinato alto spin
(6cHS) e del 6-coordinato basso
spin ( 6cLS).
d
H O
2
d x 2 -y 2
dz2
xz , d yz (d
d xy
N
d x 2 -y 2
dz2
Q
S=3
RR frequencies of the core size marker bands for the ferric and
ferrous hemes, together with the indication of the a wavelength
region where they are enhanced, b mode number and symmetry
species.
exc.a
modeb
Soret
4 (A1g)
3 (A1g)
11 (B1g)
2 (A1g)
19 (A2g)
10 (B1g)
Soret
,
Soret
,
,
Fe2+
-----------------------5c-HSd
6c-LS
1604
Fe3+
-------------------------------------6c-HS
5c-HS 6c-LS
1357
1359
1370
1373
1373
1471
1493
1480
1491
1502
1547
1539
1545
1553
1562
1562
1584
1559
1570
1579
1550
1583
1560
1571
1586
1617
1610
1626
1640
5-c, 6-c: 5-, and 6-coordinate heme; HS, LS: high and low spin
heme.
Spettro RR nella regione 150-600 cm-1
• Vibrazioni di stiramento Fe-Legante: per es.
(Fe2+-Im), (Fe2+-CO), (Fe3+-OH), (Fe3+-CN)
le cui frequenze sono sensibili alla presenza di
legami ad idrogeno tra il legante e residui
aminoacidi della cavità
• Le vibrazioni di piegamento dei sostituenti
periferici (vinili e propionili) le cui frequenze
variano a seconda della presenza di legami ad
idrogeno (propionili) o della orientazione del
doppio legame rispetto ai doppi legami dell’eme
(vinili)
In conclusione:
Gli spettri UV-Vis delle emoproteine riflettono variazioni della
struttura elettronica della porfirina.
La configurazione elettronica dell’atomo di Fe perturba la
struttura elettronica della porfirina ed è influenzata a sua
volta dalle interazioni tra il Fe ed i suoi leganti
Perciò lo spettro UV-Vis dà informazioni sullo stato di
ossidazione, di spin e di coordinazione del Ferro
Lo spettro RR da’ informazioni dettagliate sull’atomo di Ferro
e sulla presenza di interazioni tra l’eme ed I residui della
cavità ematica
SERS
(Surface Enhanced Raman Scattering)
• SERS is a surface sensitive technique that
results in the enhancement of Raman scattering
by molecules adsorbed on rough metal surfaces.
• The enhancement factor can be as much as
1014 – 1015, which allows the technique to be
sensitive enough to detect single molecules.
From Raman to SERS
• The energy of a vibrational mode depends on
the molecule’s structure and environment.
– Raman spectra of different molecules are unique
• Raman intensity lines are 0.001% (at most) of
the source intensity.
• The intensity can be increased by 103 – 106
orders of magnitude if the sample is adsorbed
on the surface of colloidal metal particles.
How does SERS work?
• The mechanism of SERS is not completely understood.
– Electromagnetic enhancement
• Proposed by Jeanmarie and Van Duyne in 1977
– Chemical enhancement
• Proposed by Albrecht and Creighton in 1977
• Electromagnetic enhancement
– Arises from the presence of surface plasmons on the
substrate.
• Surface plasmons are electromagnetic waves that propagate
along the surface parallel to the metal/dielectric interface.
How does SERS work?
• Surface plasmons are generated when the incident
light excites the electron gas of the metal.
• When a substrate is placed in the proximity of the
plasmon, it experiences an enhanced
electromagnetic field and produces an enhanced
scattered Raman field.
• Chemical enhancement
– Involves charge transfer between the chemisorbed
species and the metal surface
• This enhancement is generally less than a factor of 10
How does SERS work?
•
SERS substrates commonly used
– Silver (Ag), gold (Au) and copper (Cu)
– The energy required to generate plasmons matches the light
sources typically used in Raman spectroscopy
• Surface preparations
– Largest enhancements for rough surfaces of 10 – 100 nm
What information is obtained using
SERS?
• SERS is used to investigate the vibrational
properties of adsorbed molecules yielding
structural information on the molecule and its
local interactions.
• Uniquely identifies molecules.
• Enables the detection of individual molecules.
Why use SERS?
•
•
•
•
High sensitivity
Specificity
Valuable tool for analyzing mixtures
Low-power lasers and low magnification optics
are suitable to acquire SERS spectra in very
short acquisition times (typical ~10 s).
• Many applications—biochemistry, chemical
manufacturing, environmental detection,
forensics.
Raman scattering (SERS) methodology offers a great promise for
simplified, sensitive detection of biomolecular interactions and
several advantages in early diagnostic over the previously
Surface-enhanced Raman scattering (SERS)-based sensor
was developed for the detection of the oncoprotein c-Jun at
nanomolar levels. c-Jun is a member of the bZIP (basic
zipper) family of dimeric transcriptional activators, and its
overexpression has been associated with carcinogenic
mechanisms in several human cancers.
Imaging in vivo
Tecniche Chirottiche
Finora, nella interazione tra radiazione e materia, la
nostra attenzione si è focalizzata sulla materia:
l’energia trasferita dalla radiazione elettromagnetica
alle molecole provocava la loro promozione dallo stato
fondamentale a stati eccitati (elettronici, vibrazionali,
rotazionali).
Ora esaminiamo quali effetti ha tale interazione
radiazione elettromagnetica-materia sulla radiazione
trasmessa
Radiazione EM non Polarizzata
La radiazione EM è un’onda trasversa consistente in un campo
elettrico e in uno magnetico oscillanti e mutuamente
perpendicolari.
In generale l’oscillazione
non ha luogo in un piano
fisso.
La radiazione è non
polarizzata.
Quando la radiazione EM è
non polarizzata, il piano di
oscillazione varia nel tempo
in modo casuale.
Polarizzazione della Radiazione EM
Un filtro polarizzatore trasforma la radiazione non polarizzata in
radiazione polarizzata in un piano. Un esempio è un filtro
Polaroid. Esso è costituito da filari paralleli di polimeri. Solo la
luce polarizzata in una direzione passa, mentre le altre
componenti vengono assorbite.
Luce piano polarizzata
E
M
Direction of propagation
E vectors
Polarizer
Direction of propagation
• Polarizzazione lineare
lungo l’asse y
• Polarizzazione lineare
lungo l’asse x
In queste e nelle successive animazioni viene mostrato il
solo campo elettrico; il campo magnetico è perpendicolare a
quello elettrico e alla direzione di propagazione dell’onda
Se si sovrappongono due onde piane polarizzate linearmente lungo due
assi perpendicolari e sfasate tra loro si ottiene un’onda polarizzata
circolarmente
L’animazione mostra la sovrapposizione di due onde aventi la
stessa ampiezza, polarizzate su due assi perpendicolari tra
loro e sfasate di 900
Il vettore polarizzazione non è più costante in direzione ma
ruota con una certa velocità angolare
Polarizzazione circolare destra e sinistra
• Polarizzazione destra
• Polarizzazione sinistra
(l’angolo di sfasamento è +900), il
(l’angolo di sfasamento è -900), il
vettore polarizzazione ruota in
vettore polarizzazione ruota in
senso orario
senso antiorario
l’onda avanza
uscendo dallo
schermo
• Consideriamo due onde polarizzate circolarmente, una
destra e l’altra sinistra, aventi la stessa ampiezza;
• La risultante della loro sovrapposizione è un’onda
polarizzata piana
In generale una qualsiasi onda polarizzata
linearmente può essere scomposta nella somma di
due onde polarizzate circolarmente una destra e
l’altra sinistra aventi la stessa ampiezza
Onda polarizzata piana in un mezzo
All’ingresso del
mezzo
All’uscita del
mezzo
L’onda elettromagnetica attraversa un mezzo con indice di rifrazione n > 1;
La velocità dell’onda diminuisce, ma la frequenza resta costante, per cui diminuisce la
lunghezza d’onda;
L’onda in uscita risulta sfasata rispetto a quella che si avrebbe attraverso il vuoto (PS
nell’esempio la lunghezza del campione è presa un multiplo della lunghezza d’onda)
Onda polarizzata circolarmente in un mezzo
All’ingresso del
mezzo
All’uscita del
mezzo
Come prima la luce rallenta nel mezzo, diminuisce la lunghezza d’onda, ed esce sfasata dal
mezzo (nell’animazione si è preso il campione di lunghezza multipla della λ nel vuoto, per
cui, in assenza del mezzo, l’onda in uscita sarebbe stata in fase con quella in ingresso);
l’ampiezza resta costante (si è ipotizzato un assorbimento nullo)
Equazioni di FRESNEL
L’equazione di Fresnel correla l’angolo misurato alla differenza
degli indici di rifrazione per la luce circolarmente polarizzata
destrorsa e sinistrorsa
l
( nL nR )
180 l
espresso in radianti
l espresso in cm
espresso in gradi
( nL n R )
l espresso in dm
L’animazione che segue mostra cosa accade quando un’onda piana
polarizzata linearmente attraversa un mezzo che non rallenta la
componente circolare sinistra (in rosso), ma rallenta la componente
circolare destra (verde)
L’onda in uscita risulta essere ancora un’onda polarizzata
linearmente, ma l’asse del campo elettrico non è più verticale,
bensì risulta ruotato di un certo angolo (rotazione ottica)
Apparato sperimentale
Jasco J-810 Circular Dichroism System
Gli spettri CD vengono ottenuti con
spettropolarimetro CD mostrato in Figura.
un
dicrografo
o
47
POLARIMETRO
= rotazione osservata in gradi
t
c l
c = concentrazione in g/ml
l = lunghezza del campione in dm
t = temperatura in centigradi
= lunghezza d’onda (linea D del sodio)
Per liquidi puri la densità, d, rimpiazza la concentrazione nella precedente formula
Rotazione specifica molecolare
M t
[ ]t Pesomolecolare
[ ]
100
Vantaggi del metodo polarimetrico
Il valore di [] è un dato analitico che caratterizza ogni composto
chirale e pertanto consente un confronto con i dati già presenti in
letteratura
• Costituisce uno standard di riferimento per i nuovi composti di
origine sia naturale sia sintetica
Svantaggi del metodo polarimetrico
• Occorrono quantità relativamente grandi di sostanza
• Il prodotto chirale deve essere isolato e purificato
• La determinazione analitica di [] è influenzata da diversi fattori tra cui:
temperatura, solvente, lunghezza d’onda, impurezze sia otticamente attive
sia inattive
•
Dicroismo circolare
• Alcuni materiali hanno la seguente proprietà:
assorbono luce polarizzata destra in modo diverso da come
assorbono la luce polarizzata sinistra
• Per questo motivo, se un’onda polarizzata linearmente li attraversa,
questa cambia le sue proprietà perché verranno assorbite in modo
diverso la sua componente circolare destra e quella circolare
sinistra
la quantità
CD = AL – AR
misurata è
dove:
la
differenza
tra
le
assorbanze:
AL è l’assorbanza della luce polarizzata sinistra e
AR è l’assorbanza della luce polarizzata destra
la quantità di interesse è la differenza tra i coefficienti di
estinzione molare
CD = εL- εR (cm-1 M-1); quest’ultima è
indipendente dalla concentrazione, ma dipende solo dalla natura del
soluto
L’animazione che segue mostra cosa accade ad un’onda polarizzata
linearmente (celeste) quando attraversa un mezzo (ipotetico) che
non assorbe affatto la componente circolare sinistra (in rosso), ma
assorbe molto la componente destra (in verde)
All’ingresso
del mezzo
All’uscita del
mezzo
All’ingresso
del mezzo
All’uscita del
mezzo
L’onda in uscita è data dalla sovrapposizione di un’onda
polarizzata destra (in verde) fortemente ridotta, e una
polarizzata sinistra con ampiezza uguale a quella in ingresso; la
risultante non è più un’onda piana polarizzata linearmente;
il vettore polarizzazione E dell’onda in uscita (in celeste) ruota
descrivendo un’ellisse;
il risultato quindi è un’onda polarizzata ellitticamente
Naturalmente è insolito per un materiale non assorbire affatto una
componente circolare; i materiali reali normalmente assorbono, in
misura diversa, entrambe le componenti (destra e sinistra)
Ellitticità
Si definisce ellitticità θ l’arcotangente del rapporto tra l’asse
maggiore e l’asse minore dell’ellisse descritta dal vettore
polarizzazione della luce uscente dal mezzo
ER EL
tg
ER EL
Tra CD e ellitticità esiste una relazione:
180
ln10 AL AR
4
Con θ in gradi
Per poter comparare i risultati tra due diverse sostanze, è necessario renderli
indipendenti dalla concentrazione; definiamo l’ellitticità specifica nel seguente
modo:
S
c l
dove θ è l’angolo di ellitticità in gradi, c è la concentrazione in g/ml, l è il
cammino ottico in dm (decimetri, è una tradizione centenaria degli spettroscopisti!)
Più spesso viene riportata l’ellitticità molare:
S M
100
deg M g
100 c g cm3 l 101 cm
10 103
c
M
moli
litro l cm
100
C l
deg M-1 cm-1
dove M è il peso molecolare, C è la concentrazione in moli/litro e l è il
cammino ottico in cm;
per i biopolimeri è più conveniente esprimere i dati in termini di media sui
residui piuttosto che in quantità molari, per cui M sarà il peso medio per
residuo
100 θ
θ
Cl
deg M-1 cm-1
L’ellitticità molare [θ] può essere espressa anche come
differenza tra i coefficienti di estinzione molare della luce
circolare sinistra e destra
100 θ
32,98Δε 32,98(ε L ε R )
θ
Cl
Dicroismo circolare e birifrangenza circolare
Normalmente i materiali in natura non mostrano CD o CB
separatamente, ma si verificano entrambi i fenomeni
contemporaneamente;
L’animazione che segue mostra cosa accade ad un’onda piana
polarizzata linearmente che attraversa un mezzo che presenta sia
dicroismo circolare che birifrangenza circolare
La componente sinistra (in rosso) attraversa il mezzo immutata,
mentre la componente destra (in verde) viene attenuata e
rallentata
La luce in uscita risulta aver subito due modificazioni:
a causa del dicroismo circolare è diventata ellittica ()
a causa della birifrangenza circolare l’asse maggiore di
tale ellisse è ruotato rispetto alla polarizzazione in
ingresso (rotazione ottica )
l’ellitticità della luce in uscita dipende dalla differenza
di assorbimento tra la luce polarizzata circolarmente
destra e quella sinistra (AL – AR)
l’angolo di cui è ruotata l’ellisse è determinato dalla
differenza degli indici di rifrazione della luce destra
rispetto a quella sinistra (nL – nR)
Rotazione ottica
= angolo di rotazione dell’asse maggiore dell’ellisse di polarizzazione
rispetto all’asse della luce incidente
Rotazione ottica come funzione della lunghezza d’onda è chiamata
Optical Rotatory Dispersion (ORD)
Birifrangenza circolare nR ≠ nL
ORD: = 180(nL - nR)l/
Ellitticità
tgθ = rapporto tra asse minore ed asse maggiore
Dicroismo circolare (CD) |AR| ≠ |AL|
Ellitticità: θ = 180 (AL - AR)ln10/4
La dipendenza dalla lunghezza d’onda della Rotazione
Ottica e del Dicroismo Circolare in prossimità del
massimo di assorbimento prende il nome di
EFFETTO COTTON
Se il campione subisce solo transizioni
elettroniche π→π* la forma dello spettro CD
è in relazione con lo spettro di assorbimento
nel modo mostrato in figura;
A) Spettro di assorbimento
B) Spettro CD
C) Spettro ORD
Si nota come lo spettro CD segue
abbastanza fedelmente (a parte il segno) lo
spettro di assorbimento
Lo spettro ORD appare come la derivata
(cambiata di segno) di quello CD; inoltre si
nota che lo spettro ORD ha delle code
piuttosto lunghe, per cui si misurano segnali
ORD anche al di fuori della banda di
assorbimento
A differenza della rotazione ottica, il
dicroismo circolare si verifica solo in
corrispondenza di un fenomeno di
assorbimento.
L’effetto Cotton positivo (curve superiori in Figura) si ha in corrispondenza
di una banda CD positiva.
L’effetto Cotton negativo (curve inferiori) si ha in corrispondenza di una
banda CD negativa.
La lunghezza d’onda in cui la rotazione ottica vale zero corrisponde
approssimativamente al massimo nell’ellitticità.
Sostanze otticamente attive
Le sostanze di interesse che hanno interazione con la luce
(assorbimento e rifrazione) si dicono cromofori
Le sostanze che presentano dicroismo circolare
birifrangenza (CB) si dicono otticamente attive
(CD)
e
Affinché la sostanza sia otticamente attiva, le sue molecole devono
presentare una dissimetria nella loro struttura, tale da ruotare il
piano di polarizzazione della luce. Nell’ambito delle molecole
dissimetriche rientrano le molecole dotate di chiralità
Le molecole dissimmetriche interagiscono con il piano della luce polarizzata
con modalità tali che le onde R e L sono rifratte e assorbite in modo diverso..
L’assorbimento differenziato delle onde R e L comporta una variazione tale
della loro ampiezza per cui il fascio di luce trasmesso è polarizzato
ellitticamente piuttosto che circolarmente
Le molecole “destro-rotatorie” sono tali da produrre un
maggior rallentamento della luce polarizzata circolare
sinistra e quindi fanno viaggiare più velocemente la luce
circolare destra; il vettore polarizzazione viene
ruotato di un certo angolo in senso orario;
Le molecole “sinistro-rotatorie” produrranno un
maggior rallentamento della luce polarizzata circolare
destra; il vettore polarizzazione viene ruotato di un
certo angolo in senso antiorario;
La stessa dissimmetria si avrà per l’assorbimento delle due
componenti circolari, per cui molecole chirali determineranno
dicroismo circolare (sono otticamente attive);
Un’alta sorgente per un segnale CD è la
disposizione chirale dei cromofori in una
struttura 3D; un’elica ha un verso di
avvitamento (orario o antiorario), e la sua
immagine speculare non coincide con se
stessa: in pratica un’elica è sempre
chirale; se un gruppo di cromofori è
disposto in un configurazione ad elica (es.
gli aminoacidi di una proteina), essi
produrranno un segnale CD.
Infine bisogna considerare la possibilità di interazione tra cromofori
vicini nello spazio; per esempio il gruppo eme è otticamente non attivo se
isolato, ma le emoproteine presentano uno spettro CD molto ricco sopra i
300 nm: ciò è dovuto all’accoppiamento dipolo-dipolo che coinvolge le
transizioni dell’eme e le transizioni π π* della proteina.
Apparato sperimentale
Jasco J-810 Circular Dichroism System
Gli spettri CD vengono ottenuti con
spettropolarimetro CD mostrato in Figura.
un
dicrografo
o
65
La radiazione, resa monocromatica da un monocromatore, viene
polarizzata linearmente e passa poi attraverso un modulatore
fotoelastico che genera alternativamente luce polarizzata circolarmente
a sinistra e a destra con una certa frequenza di modulazione.
La radiazione così modulata passa attraverso il campione e viene rivelata
dal fotomoltiplicatore. Il segnale risultante, anch’esso modulato alla
stessa frequenza, fornisce la differenza di assorbanza delle due
componenti polarizzate circolarmente, a quella lunghezza d’onda.
Variando la lunghezza d’onda si ottiene lo spettro CD.
Modulatore elettro-ottico (d),
Preparazione del campione
1. Scegliere il giusto tampone
Molti campioni di proteine sono sciolti in tamponi contenenti
detergenti, EDTA (acido etilendiamminotetraacetico) o alte
concentrazioni di Sali.
Questi tamponi non sono ottimali, in quanto non sono trasparenti
alla luce nella regione tra 180-210 nm, cruciale per l’analisi delle
proteine.
In generale vanno evitate tutte quelle sostanze che possono
assorbire nell’intervallo delle λ di interesse (per le proteine:
180nm – 280nm)
68
Calibrazione dello strumento di misura
Per una corretta misura spettroscopica è necessario calibrare
periodicamente lo strumento; assumiamo che la scala delle lunghezze
d’onda sia sufficientemente accurata, per cui si va a calibrare
l’assorbanza alle varie λ;
il composto normalmente usato per la calibrazione è l’acido d-10Camphorsulfonico (d sta per destro), il cui spettro CD fornisce due
punti di calibrazione caratteristici: uno negativo a 192.5 nm e uno
positivo a 290.5 nm
Proprietà CD dell’acido d-10-Camphorsulfonico in acqua
69
The molar CD spectrum of d-10-Camphorsulfonic acid in water
(1mg/ml, 1mm cuvette)
70
La calibrazione viene fatta normalmente con cuvette da 1cm;
se vengono usate cuvette con un cammino ottico diverso bisogna
ripetere la calibrazione, e verificare che la nuova misura CD sia
proporzionale alla nuova lunghezza:
per esempio se si vogliono usare cuvette con cammino ottico 0.5
cm, si dovrebbe osservare una riduzione nell’intesità dello
spettro CD di un mezzo rispetto a quello delle cuvette da 1 cm.
71
CD e Molecole Biologiche
Quasi tutte le molecole sintetizzate da organismi viventi sono
otticamente attive.
L’attività ottica è un elemento così
caratteristico della vita, almeno come noi la conosciamo, da
essere uno dei criteri usati per giudicare, p.es., se meteoriti
contengano evidenze di vita presente da qualche parte
dell’universo.
L’attività ottica delle molecole piccole nasce dalla loro mancanza
di simmetria, in particolare per la presenza di atomi di carbonio
asimmetrici e dall’effetto che essi hanno sui cromofori vicini.
72
Applicazioni CD in biologia
•
•
•
•
•
•
Stima della struttura secondaria di una proteina
Termodinamica di una proteina
Ligand binding (costanti di legame)
Effetti del solvente su una macromolecola
Stima della struttura degli acidi nucleici
Termodinamica degli acidi nucleici
Comune a tutte queste analisi CD è la presenza di cromofori chirali;
il loro particolare arrangiamento o la variazione di disposizione a
seguito di perturbazioni sperimentali (cambi di solvente, aumento di
temperatura, …) possono essere monitorati tramite CD
73
Proteine
Le proteine assorbono la luce nella regione dell’ultravioletto; le
principali fonti di assorbimento sono
1. il legame peptidico
2. la catena laterale (per alcuni a.a.)
3. l’eventuale gruppo prostetico
L’assorbimento della luce relativo al legame peptidico è dovuto a
possibili transizioni tra gli stati elettronici degli elettroni di
legame
In realtà anche i residui degli aminoacidi aromatici (triptofano,
tirosina, fenilalanina) danno un contributo in questa regione dello
spettro, ma tale contributo è, nella maggior parte dei casi, molto
minore rispetto al legame peptidico (potrebbe diventare
significativo nel caso improbabile in cui la maggioranza degli a.a.
74
della proteina siano di tipo aromatico)
Assorbimento del legame peptidico
L’assorbimento della luce relativo al legame peptidico è dovuto a possibili
transizioni tra gli stati elettronici degli elettroni di legame; senza
scendere nel dettaglio, interessa qui ricordare le lunghezze d’onda delle
energie alle quali avvengono tali transizioni, che corrispondono poi alle λ di
assorbimento:
n → π* centrato attorno a 220 nm (intensità debole, ε ≈ 100)
π → π* centrato attorno a 190 nm (molto intenso, ε ≈ 7000)
75
Assorbimento delle catene laterali
Le catene laterali alifatiche degli a.a.
hanno un assorbimento relativamente
basso; inoltre tale assorbimento
avviene per lunghezze d’onda vicine a
quelle del legame peptidico, per cui il
loro
spettro
è
parzialmente
perturbato da quello del peptidico;
Lo spettro degli a.a. aromatici
(triptofano,
tirosina,
fenilalanina)
presenta un picco intorno a 280 nm,
quindi è sufficientemente spostato
rispetto a quello del legame peptidico;
l’intensità è comunque molto più bassa
rispetto a quella del legame peptidico
76
Amide Chromphore
• n * centered around 220 nm
• * centered around 190 nm
n -> * involves non-bonding electrons of O
of the carbonyl;
-> * involves the -electrons of the
carbonyl
80
Random coil
positive at 212 nm (->*)
negative at 195 nm (n->*)
Sheet
negative at 218 nm (->*)
positive at 196 nm (n->*)
helix
positive at 192 nm >*
negative at 209 nm (->*)
negative at 222 nm is red
shifted
(n->*)
Esempio: spettro CD della mioglobina
82
Analisi dei dati
Nell’analisi dello spettro misurato, si assume che le proprietà
ottiche dei diversi cromofori presenti nel campione siano additive,
per cui si può scrivere:
n
X ( ) f i X i( )
i 1
dove X(λ) è il CD medio per residuo (εL- εR oppure [θ]), fi è la
frazione della i-esima componente, e Xi(λ) è il corrispondente
valore di CD per quella componente;
83
Struttura secondaria delle proteine
Uno dei maggiori impieghi della spettroscopia CD è la stima della presenza
delle diverse strutture secondarie di una proteina folded;
Ricordiamo le principali strutture secondarie di una proteina:
α-elica, β-sheet, β-turn, random-coil
per cui la X(λ) si può scrivere:
X ( ) f H X H( ) f X ( ) f t X t ( ) f R X R ( )
Note le Xi(λ) a diverse frequenze (in questo caso minimo quattro), si
possono usare come base per risolvere il sistema e trovare i diversi
coefficienti fi che daranno la composizione della proteine rispetto alle
diverse strutture secondarie
84
-elica
85
β-sheet
86
β-turn
87
Cartoon drawings of:
A) triosephosphate isomerase (H:0.52, S:0.14, T:0.11, O:0.23);
B) hen egg lysozyme (H:0.36, S:0.09, T:0.32, O:0.23);
C) myoglobin (H:0.78, S:0.0, T:0.12, O:0.10);
D) chymotrypsin (H:0.10, S:0.34, T:0.20, O:0.36).
Secondary structures are color coded
red: helix α; green: strand β, and yellow: other.
88
Circular dichroism spectra of
triosephosphate isomerase (H:0.52, S:0.14, T:0.11, O:0.23),
hen egg lysozyme (H:0.36, S:0.09, T:0.32, O:0.23),
myoglobin (H:0.78, S:0.0, T:0.12, O:0.10),
chymotrypsin (H:0.10, S:0.34, T:0.20, O:0.36).
89
Spettri di base e spettri di riferimento per la
struttura secondaria delle proteine
Esistono due possibilità per avere degli spettri di base da
utilizzare per la stima della struttura secondaria di una proteina:
1. spettri da polipeptidi modello (sintetici)
2. spettri da proteine modello (naturali) di cui è nota per
altre fonti la struttura secondaria
n
X ( ) f i X i( )
i 1
90
Differenza tra spettri di riferimento e
spettri di base
Un data set di riferimento di una proteina è uno spettro CD
normalizzato (ellitticità o CD molare per residuo) di una
proteina (o un polipeptide) di cui è nota la struttura 3D;
dai data set di più proteine si può ottenere una base Xi(λ) da
usare per determinare le frazioni fi di una proteina incognita
91
Spettri di base da polipeptidi modello
La polilisina (Lys)n è uno dei possibili polipeptidi usati come modello,
utile in quanto assume diverse strutture secondarie variando
temperatura e PH della soluzione; in una soluzione acida si comporta
come un random coil, aumentando il PH oltre 10 transisce verso una αelica, riscaldando a 500 e poi raffreddando diventa un β-form.
Nel 1969 Greenfield e Fasman proposero un metodo per la stima della
quantità di α-elica (H), β-form, e forma disordinata (Random) in una
proteina utilizzando i tre spettri di riferimento della polilisina:
X ( ) f H X H( ) f X ( ) f R X R( )
Utilizzando tre misure a diversi λ, si ottiene un sistema di equazioni
lineari nelle tre incognite fH, fβ, fR;
Per migliorare la stima si possono prendere più di tre misure a diversi
λ, e poi ricavare le tre frazioni incognite tramite procedure
statistiche
92
Spettro CD della polisina
93
Altri polipeptidi modello sono stati proposti da vari ricercatori nel
corso degli anni:
Rosenkranz e Scholtan usarono la poliserina (Ser)n (1971)
S. Brahms e J Brahms introdussero i β-turns (t) (1980) usando
polipeptidi diversi come modello per le diverse strutture
X ( ) f H X H( ) f X ( ) f t X t ( ) f R X R ( )
S. Brahms e J Brahms usarono come modello:
il CD della mioglobina (79% α-elica, 6% β-turns, no β-form) per α-elica
(Lys-Leu)n in 0.1 M NaF a PH7 per la β-form
(Pro-Lys-Leu-Lys-Leu)n per il random-coil
L-Pro D-Ala, (Ala2-Gly2)n e Pro-Gly-Leu per il β-turns
94
Circular dichroism spectra of "pure" secondary structures. Redrawn
from Brahms & Brahms, 1980.
95
Debolezza del metodo con i polipeptidi
Ci sono due punti deboli nei metodi che usano polipeptidi come
base per i segnali CD:
1. I segnali CD di α-elica e β-sheet sono funzione della
lunghezza dell’elica; i polipeptidi sono di solito più lunghi dei
tratti di struttura α e β presenti nelle proteine globulari
2. La struttura terziaria di una proteina è costituita da regioni
di struttura secondaria impacchettate; questo ha effetti
sul segnale CD di cui non si tiene conto attraverso i
polipeptidi
96
In generale i metodi mostravano una buona predizione delle strutture α, una
discreta predizione delle strutture β-form, una scarsa predizione dei β-turn
Le recenti tecniche per la determinazione delle strutture secondarie
raggiungono livelli di accuratezza pari a 0,97 per l’α-elica 0,75 per il βsheet, 0,50 per il β-turn, 0,79 per le altre strutture (Manavalan &
Johnson, 1987)
DICHROWEB
http://www.cryst.bbk.ac.uk/cdweb/html/home.html
97










