I_prova_2002

I Prova in itinere corso di Fisica 4 A.A. 2001/2
NOME………….....….
COGNOME……………........………............ VOTO
Esercizi numerici
1) La luce rossa del sole, assunta come un’onda elettromagnetica piana la cui ampiezza di campo
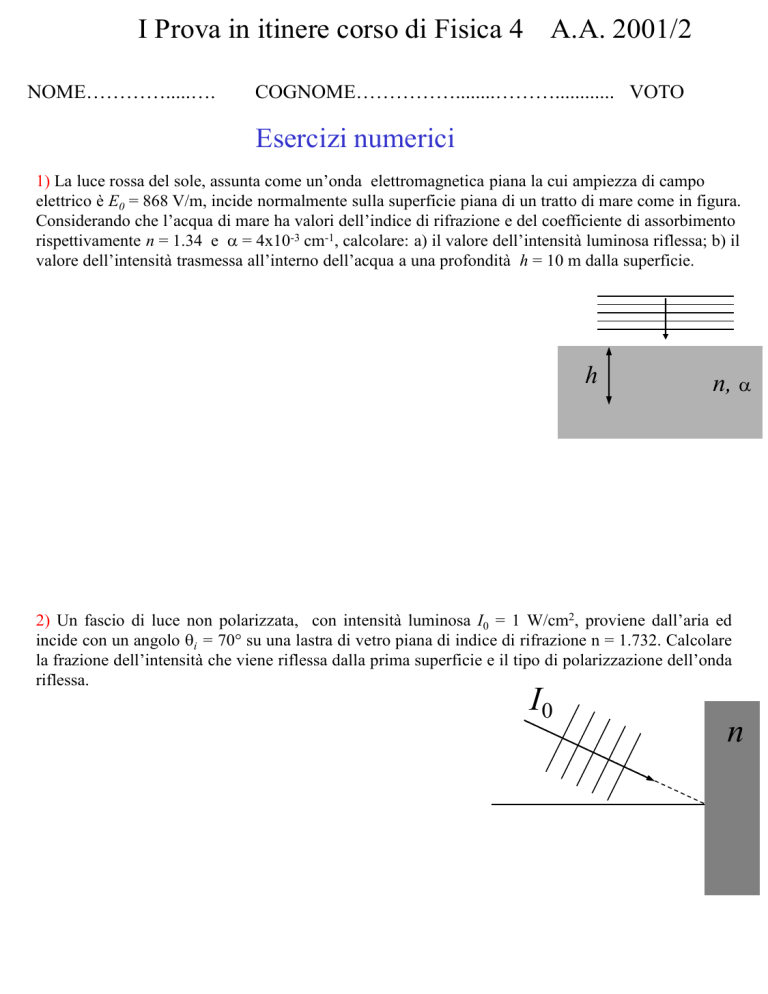
elettrico è E0 = 868 V/m, incide normalmente sulla superficie piana di un tratto di mare come in figura.
Considerando che l’acqua di mare ha valori dell’indice di rifrazione e del coefficiente di assorbimento
rispettivamente n = 1.34 e  = 4x10-3 cm-1, calcolare: a) il valore dell’intensità luminosa riflessa; b) il
valore dell’intensità trasmessa all’interno dell’acqua a una profondità h = 10 m dalla superficie.
h
n, 
2) Un fascio di luce non polarizzata, con intensità luminosa I0 = 1 W/cm2, proviene dall’aria ed
incide con un angolo i = 70° su una lastra di vetro piana di indice di rifrazione n = 1.732. Calcolare
la frazione dell’intensità che viene riflessa dalla prima superficie e il tipo di polarizzazione dell’onda
riflessa.
I0
n
3) In un esperimento di doppia fenditura si trova che la luce blu di lunghezza d’onda 1 = 450 nm
genera un massimo del secondo ordine in una certa posizione dello schermo. Per quale lunghezza
d’onda di luce visibile (400 nm < VIS < 750 nm) si avrebbe un minimo nella stessa posizione?
P
4) Uno dei fasci di un interferometro passa attraverso una cella di vetro cava lunga l = 1.3 cm.
Immettendo lentamente un gas nella cella si osserva il passaggio di 236 frange scure. La lunghezza
d’onda della luce è  = 610 nm. Calcolare l’indice di rifrazione del gas assumendo che il resto
dell’interferometro sia sotto vuoto.
M1
l
sorgente
M2
5) A che distanza reciproca t devono essere poste due fenditure, ciascuna di apertura D = 0.23 mm e
illuminate da luce violetta di lunghezza d’onda  = 415 nm, affinché i primi minimi di intensità da
diffrazione si sovrappongano su uno schermo distante d = 2.55 m?
t
P
d
Quesiti
A) Scrivere l’espressione del campo elettrico di un’onda elettromagnetica monocromatica piana
polarizzata circolarmente che si propaga lungo la direzione z in un mezzo con indice di rifrazione n.
B) Da cosa è prodotto il “tremolio” delle immagini osservate vicino ad una sorgente calda?
C) Quali sono le condizioni sulla luce che incide sulle fenditure per ottenere interferenza alla Young?
D) Da cosa è prodotta l’iridescenza delle lamine sottili?
E) Cosa succede ad un breve impulso di luce quando attraverso un mezzo dispersivo e perché?
F) Come è definito “l’angolo limite”?
Soluzioni
1)
I0 
E0 2
2Z0
 1000 W
I l  I 0 1  R e
h
 n 1
 RI 0  
 I 0  21.1 W 2
m
 n 1
2
m2
I rifl
  n 1 2 
 1  
  exp  0.004 1000I 0  17.9 W 2
m
  n  1  
2)
Trattandosi di luce non polarizzata:
poiché: sinθ r 
R
quindi:

I' i 1
 R   R // 
Ii 2
n1
1
sinθi 
sin 70  θ r  32.86
n2
1.732
sin 2 θi  θ r 
 0.38
sin 2 θi  θ r 
R //

I' i
1  sin 2 θi  θ r  tg 2 θi  θ r 
  2

Ii
2  sin θi  θ r  tg 2 θi  θ r 
tg 2 θi  θ r 
 0.03
2
tg θi  θ r 

  0.207

la luce riflessa è parzialmente polarizzata perpendicolarmente al piano
di incidenza
3)
I = Imax se:
da cui:
sin θ  m1
1
D
(2m2  1)  2


 m1 1  2 1
2
D
D
D
m  0, 1, 2, 3, . . . . 
4)
I = 0 se sin θ 
 2 VIS 
 2 
(2m2  1)  2
2
D
4
1
(2m2  1)
4
1  600 nm
3
la condizione sulla differenza di cammino ottico per osservare l’m-esima
frangia scura è:
s  s'  (2m  1)
0
2
si osserva il passaggio ad un’altra frangia scura ogni volta che s-s’ varia di
, quindi:
236  0  s  s'  2(n  1)l
236
6.1  107
n 1
 0  1  236
 1.0055
2l
2  1.3  10 2
5)
dalla figura, per costruzione, e dalla legge di diffrazione di Fraunhofer:
ymin  d

t

D
2

t 
2
d  9.2 mm
D