MICROECONOMIA ED ECONOMIA SPERIMENTALE:
LE SCELTE E I MERCATI IN LABORATORIO
INTRODUZIONE
di Ivan Moscati e Giuseppe Attanasi
1. Il modello di domanda e offerta: la versione da manuale
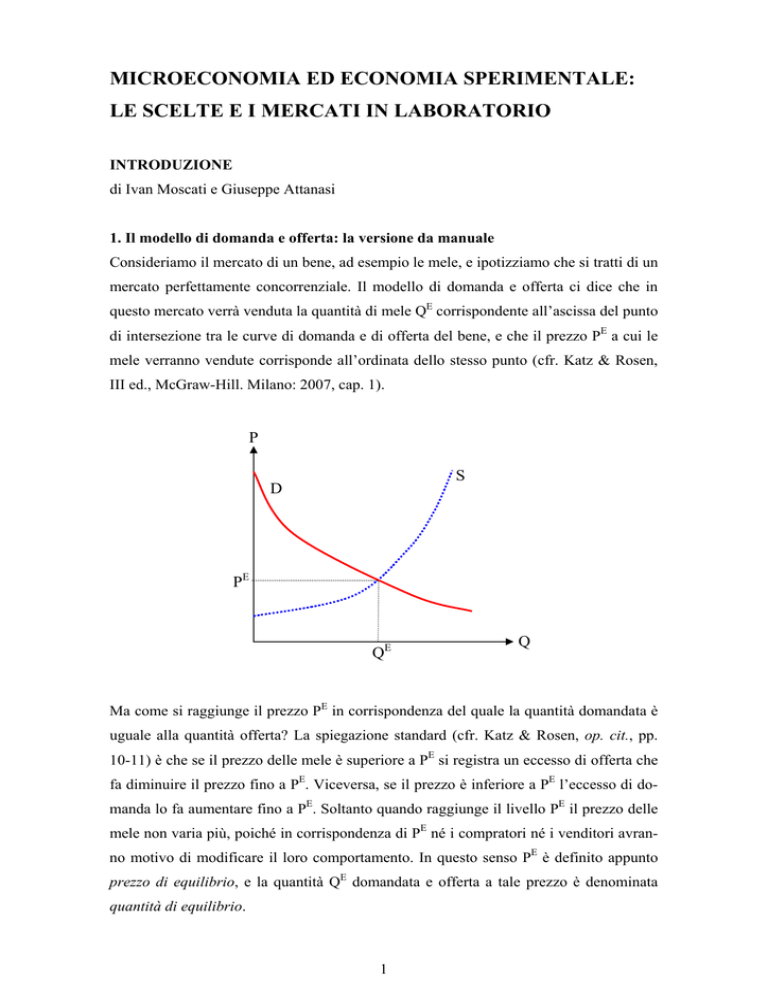
Consideriamo il mercato di un bene, ad esempio le mele, e ipotizziamo che si tratti di un
mercato perfettamente concorrenziale. Il modello di domanda e offerta ci dice che in
questo mercato verrà venduta la quantità di mele QE corrispondente all’ascissa del punto
di intersezione tra le curve di domanda e di offerta del bene, e che il prezzo PE a cui le
mele verranno vendute corrisponde all’ordinata dello stesso punto (cfr. Katz & Rosen,
III ed., McGraw-Hill. Milano: 2007, cap. 1).
P
S
D
PE
QE
Q
Ma come si raggiunge il prezzo PE in corrispondenza del quale la quantità domandata è
uguale alla quantità offerta? La spiegazione standard (cfr. Katz & Rosen, op. cit., pp.
10-11) è che se il prezzo delle mele è superiore a PE si registra un eccesso di offerta che
fa diminuire il prezzo fino a PE. Viceversa, se il prezzo è inferiore a PE l’eccesso di domanda lo fa aumentare fino a PE. Soltanto quando raggiunge il livello PE il prezzo delle
mele non varia più, poiché in corrispondenza di PE né i compratori né i venditori avranno motivo di modificare il loro comportamento. In questo senso PE è definito appunto
prezzo di equilibrio, e la quantità QE domandata e offerta a tale prezzo è denominata
quantità di equilibrio.
1
2. Il modello di domanda e offerta: una riconsiderazione critica
Il raggiungimento dell’equilibrio secondo il meccanismo appena descritto si basa in effetti su almeno un’ipotesi implicita, ovvero che per prezzi diversi da PE non avvengano
compravendite di mele. Appare invece del tutto verosimile immaginare che alcune mele
possano essere scambiate anche a prezzi superiori o inferiori a PE.
Facciamo un semplice esperimento mentale e consideriamo un mini-mercato delle mele,
con solo tre compratori C1, C2, e C3, e solo tre venditori V1, V2 e V 3. Immaginiamo anche che ciascun venditore porti sul mercato una sola mela, e ciascun consumatore sia interessato a comprare una sola mela. Ipotizziamo inoltre che il consumatore C1 sia disposto a pagare fino a 2 € per la mela, mentre C2 e C3 non vogliano spendere più di 1 €.
Immaginiamo poi che i venditori V1 e V2 siano disposti a vendere la loro mela se il
prezzo è maggiore o uguale a 0,5 €. V3 è invece disposto a vendere la sua mela solo se il
prezzo è almeno di 1,20 €.
Queste informazioni ci permettono di costruire le schede di domanda e offerta di questo
mini-mercato. Poiché stiamo considerando solamente quantità discrete di mele, tali
schede saranno fatte a gradini anziché essere delle curve:
P in €
S
D
2,00
1,20
P = 1,00
E
0,50
1
QE=2
Q
3
Il modello di domanda e offerta ci dice che in questo mercato verranno comprate/vendute due mele, ciascuna al prezzo di 1 €, cioè QE = 2 e PE = 1 €. Che cosa accade,
però, se permettiamo che avvengano scambi a prezzi diversi da PE?
Immaginiamo che, per qualche motivo, il prezzo vigente sul mercato sia di 0,70 € per
mela. Per 0,70 €, V1 e V2 saranno disposti a vendere la loro mela, e tutti e tre i consumatori saranno disposti a comprarla. In questa situazione appare del tutto verosimile im2
maginare che le due mele verranno vendute, senza aspettare che il prezzo salga a PE = 1
€.
Mettiamo, in particolare, che siano C2 e C3 ad acquistare le due mele. Dopo questa
compravendita, C2 e C3 andranno a casa con le loro mele, mentre V1 e V2 se ne andranno ciascuno con 0,70 € in tasca, cioè tutti e quattro usciranno dal mercato. Sul mercato
rimarranno così C1 e V3.
Al prezzo di 0,70 € anche C1 vorrebbe comprare una mela (domanda = 1), ma per quel
prezzo V3 non è disposto a vendergliela (offerta = 0). In altri termini, per P = 0,70 € c’è
un eccesso di domanda in ragione del quale il prezzo tende a salire. L’eccesso di domanda e dunque la spinta verso l’alto del prezzo continua finché il prezzo non raggiunge il livello di 1,20 € a mela. A quel punto V3 è disposto a vendere la mela a C1. Dopo
aver acquistato la mela a 1,20 €, C1 e V3 andranno ciascuno per la sua strada. Fine del
mini-mercato.
Riassumiamo i dati relativi a quantità e prezzi per questo mercato. Innanzitutto le mele
scambiate sono state 3, e non 2 come previsto dal modello di domanda e offerta. In termini percentuali ciò significa che è stata scambiata una quantità di prodotto del 50%
maggiore rispetto a quella prevista dal modello di domanda ed offerta. In secondo luogo, nessuna compravendita è stata effettuata al prezzo di equilibrio PE = 1 €: due sono
avvenute ad un prezzo inferiore (0,70 €) e una ad un prezzo superiore (1,20 €). Il prezzo
medio di compravendita delle tre mele è stato di circa 87 centesimi, cioè il 13% in meno
di PE = 1 €.
La conclusione è che le compravendite a prezzi non di equilibrio possano rendere significativamente imprecise le previsioni del modello concorrenziale di domanda e offerta
riguardo a quantità scambiate e prezzo di scambio. Molti mercati reali (si pensi ad esempio alla borsa, o proprio ai mercati rionali di frutta e verdura) hanno quasi tutte le
caratteristiche del mercato di concorrenza perfetta, tranne appunto il fatto che compravendite a prezzi diversi da PE sono possibili e magari frequenti. Ci si può allora domandare quanto sia opportuno utilizzare il modello standard di domanda ed offerta per studiare tali mercati reali. L’economia sperimentale ci permette di fare un po’ di luce su
questi problemi.
3
3. Esperimenti di mercato
L’economia sperimentale è un settore della ricerca economica che cerca di testare la validità delle teorie attraverso esperimenti. In tali esperimenti persone reali sono poste in
situazioni di scelta che rispecchiano il più possibile le situazioni in cui si trovano gli agenti dei modelli economici, in modo da verificare se le persone si comportano effettivamente come previsto dalla teoria.
Gli inizi dell’economia sperimentale risalgono agli anni Trenta del Novecento, quando
vennero effettuati alcuni esperimenti per identificare empiricamente le curve di indifferenza di un individuo. A partire dagli anni Cinquanta questo filone di ricerca è cresciuto
notevolmente e nel 2002 il premio Nobel per l’economia è stato assegnato a Daniel Kahneman e Vernon Smith proprio per le loro ricerche sperimentali.1
Un filone significativo della ricerca sperimentale ha riguardato proprio il modello di
concorrenza perfetta. Nella seconda metà degli anni Quaranta l’economista americano
Edward Chamberlin ha realizzato con i suoi studenti di Harvard una serie di esperimenti
pionieristici che sono molto simili all’esperimento mentale del mini-mercato delle mele
presentato in precedenza.2
3.1. L’esperimento di Chamberlin
Chamberlin divideva in modo casuale i suoi studenti in due gruppi, assegnando agli uni
il ruolo di compratori di un generico bene X, e agli altri il ruolo di venditori dello stesso
bene. Come i compratori e venditori di mele del nostro esperimento mentale,
nell’esperimento di Chamberlin ciascun venditore portava sul mercato una sola unità di
X e ciascun compratore era interessato ad acquistare una sola unità di X.
Ogni studente-compratore riceveva un biglietto con un numero che rappresentava la
somma massima che egli poteva spendere per l’unità di X. Tale somma era in generale
diversa da compratore a compratore ed era nota solo a Chamberlin e a chi riceveva il biglietto. Analogamente, ogni studente-venditore riceveva un biglietto con un numero che
rappresentava la somma minima di vendita per la sua unità di X; tale somma variava da
venditore a venditore e di nuovo era conosciuta solo da Chamberlin e dal possessore del
biglietto. A partire dai prezzi sui biglietti di compratori e venditori, Chamberlin era in
grado di ricostruire le schede di domanda e offerta del mercato del bene X.
1
Per una introduzione alla storia dell’economia sperimentale si può vedere A.E. Roth, Introduction to
Experimental Economics, in J.H. Kagel e A.E. Roth (a cura di), Handbook of Experimental Economics,
Princeton: Princeton University Press, 1995, pp. 3-109.
2
Vedi E.H. Chamberlin, An Experimental Imperfect Market, Journal of Political Economy, Vol. 56, No.
2 (Apr., 1948), pp. 95-108.
4
Le schede di domanda ed offerta in uno degli esperimenti di Chamberlin. Da Chamberlin 1948, p. 97.
L’obiettivo assegnato ad ogni compratore era di acquistare l’unità di X al prezzo più
basso possibile, massimizzando così la differenza tra il prezzo indicato sul suo biglietto
e il prezzo di acquisto (tale differenza corrisponde alla nozione di surplus del consumatore). Specularmente, l’obiettivo assegnato ad ogni venditore era di vendere la sua unità
di X al prezzo più alto possibile, massimizzando così la differenza tra il prezzo di vendita e il prezzo indicato sul suo biglietto (tale differenza esprime il surplus del produttore).
Gli studenti venivano poi lasciati liberi di girare per l’aula e di contrattare con le controparti allo scopo di comprare o vendere la loro unità di X al miglior prezzo possibile.
Il prezzo su cui un compratore e un venditore si accordavano dipendeva ovviamente dai
prezzi scritti sui loro biglietti, e solo casualmente coincideva con il prezzo di equilibrio
di mercato (anche perché nessuno studente conosceva le schede di domanda e offerta e
poteva quindi identificare il prezzo di equilibrio). Perciò, come nell’immaginario minimercato delle mele, anche nell’esperimento di Chamberlin molte delle compravendite
avvenivano a prezzi diversi da quello di equilibrio. In concreto, quando un compratore e
un venditore trovavano un accordo su un prezzo di compravendita andavano alla cattedra, registravano il contratto concluso, e uscivano dal mercato.
L’esperimento si riteneva concluso quando non avevano più luogo compravendite. A
quel punto Chamberlin contava il numero di unità del bene X complessivamente scambiate e calcolava il prezzo medio di compravendita al fine di confrontare questi dati con
le previsioni su quantità e prezzo di equilibrio fornite dal modello di domanda e offerta.
Chamberlin ha condotto in tutto 46 di questi esperimenti. In 42 casi su 46 la quantità di
bene X complessivamente scambiata è risultata superiore a quella prevista dal modello
5
concorrenziale di domanda e offerta. Nei restanti 4 esperimenti la quantità scambiata è
stata la stessa di quella prevista dal modello di domanda ed offerta. Questo risultato corrisponde a quello ottenuto nell’esperimento mentale del mini-mercato delle mele del paragrafo 2, dove venivano scambiate il 50% delle mele in più rispetto alla quantità di equilibrio concorrenziale. Riguardo al prezzo medio delle compravendite, in 39 esperimenti su 46 esso è risultato minore di quello previsto dal modello di domanda ed offerta, mentre in 7 esperimenti su 46 è risultato maggiore. Anche questo risultato è in linea
con quello del nostro esperimento mentale dove il prezzo medio delle mele risultava del
13% inferiore a quello di equilibrio.
È importante notare come, rispetto al nostro mini-mercato delle mele, il mercato creato
in aula da Chamberlin fosse caratterizzato da un’ulteriore differenza rispetto al modello
di concorrenza perfetta: non soltanto erano possibili scambi a prezzi diversi da quello di
equilibrio, ma compratori e venditori contrattavano sul prezzo di compravendita anziché
accettare il prezzo di mercato vigente (in effetti, sul mercato decentralizzato di Chamberlin, tale “prezzo di mercato vigente” semplicemente non esisteva). Potremmo chiamare quasi-concorrenziale un mercato che ha tutte le caratteristiche della concorrenza
perfetta, tranne che agli agenti è consentito scambiare a prezzi non di equilibrio e contrattare. Il nostro problema può allora essere posto in questi termini: se un mercato reale
sembra essere quasi-concorrenziale piuttosto che puramente concorrrenziale, quanto è
appropriato utilizzare il modello standard di domanda ed offerta per prevederne quantità
e prezzi di scambio? L’esperimento di Chamberlin sembra confermare il dubbio che le
previsioni del modello standard possano risultare significativamente imprecise.
3.2. L’esperimento di Smith
Il futuro premio Nobel Vernon Smith aveva partecipato da studente ad uno degli esperimenti di Chamberlin. Tra la metà degli anni Cinquanta e i primi anni Sessanta Smith
ha ripetuto gli esperimenti di Chamberlin con regole leggermente modificate, ottenendo
risultati sostanzialmente diversi.3
Anche Smith divideva i suoi studenti in compratori e venditori, ed assegnava ad ognuno
un bigliettino con un prezzo massimo di acquisto (se compratore) o un prezzo minimo
di vendita (se venditore) per una unità del generico bene X. Nell’esperimento di Smith,
però, compratori e venditori anziché girare per l’aula e contrattare privatamente con le
controparti, dovevano fare offerte pubbliche di acquisto o vendita, alzando la mano e
3
Vedi V.L. Smith, An Experimental Study of Competitive Market Behavior, Journal of Political Economy, Vol. 70, No. 2 (Apr., 1962), pp. 111-137 e Vol. 70, No. 3 (Jun., 1962), pp. 322-323. Trad. it. in M.
Motterlini e F. Guala (a cura di), Economia cognitive e sperimentale, Milano: Università Bocconi Editore,
2005, pp. 95-130.
6
gridando frasi del tipo: “Sono disposto a comprare un’unità di X a 3 dollari” o “Vendo
la mia unità di X a 2 dollari”.
Se qualche venditore accettava una proposta di acquisto, o qualche compratore accettava una proposta di vendita, lo dichiarava pubblicamente e sempre pubblicamente il contratto veniva chiuso. Il prezzo di compravendita, insieme ai prezzi sui biglietti del compratore e del venditore venivano scritti alla lavagna in modo che tutti potessero vederli
chiaramente. Quando le compravendite finivano, terminava la prima parte
dell’esperimento.
A differenza di Chamberlin, Smith faceva poi ripetere il gioco due o tre volte, come se
ci fossero ulteriori “giorni di mercato”. Nei nuovi giorni di mercato, a ciascun compratore veniva assegnato lo stesso prezzo massimo di acquisto e a ciascun venditore lo
stesso prezzo minimo di vendita del primo giorno.
Sebbene i mercati creati da Smith e Chamberlin siano diversi quanto a regole di contrattazione e informazione a disposizione degli agenti, entrambi sono quasi-concorrenziali
nel senso definito in precedenza. Per il mercato quasi-concorrenziale di Smith, però, le
previsioni del modello di domanda e offerta risultano molto affidabili. Infatti al ripetersi
del gioco, cioè via via che si succedono i giorni di mercato, nell’esperimento di Smith
sia la quantità scambiata che il prezzo medio di compravendita si avvicinano e poi tendono a coincidere con quantità e prezzo concorrenziali. Inoltre, nelle ripetizioni del gioco la variabilità dei prezzi di compravendita attorno al prezzo medio diminuisce, cosicché alla fine dei giorni di mercato quasi tutti i contratti si chiudono a prezzi poco più alti
o poco più bassi del prezzo di equilibrio concorrenziale. La pubblicità dell’informazione
sulle disponibilità a vendere e compare degli altri attori sul mercato, e l’esperienza acquisita attraverso la ripetizione del gioco, sembrano cioè sufficienti ad avvicinare gli
equilibri di un mercato quasi-concorrenziale a quelli di un mercato perfettamente concorrenziale.
4. Considerazioni conclusive
Torniamo alla nostra domanda: ma allora è opportuno o no utilizzare il modello concorrenziale standard di domanda ed offerta per prevedere quantità e prezzi di scambio di un
mercato reale che sia quasi-concorrenziale? Gli esperimenti di Chamberlin e Smith ci
dicono che molto dipende dalle specifiche regole di contrattazione vigenti sul mercato e
dall’informazione a disposizione degli agenti, dato che anche piccole differenze riguardo al modo in cui avviene la compravendita o sono resi noti i prezzi di chiusura dei contratti hanno una notevole influenza sugli equilibri finali raggiunti.
Molti mercati reali forse non sono perfettamente concorrenziali, ma esistono da un tem7
po sufficientemente lungo (migliaia se non milioni di giorni di mercato), e in essi compratori e venditori sono ben informati circa i prezzi di compravendita registrati in passato. Se di recente non si è verificato nessun evento che possa avere alterato significativamente le disponibilità a vendere e comprare degli attori, tali mercati quasiconcorrenziali possono essere assimilati più a quello di Smith che a quello di Chamberlin. In tali mercati il fatto che gli agenti possano scambiare a prezzi non di equilibrio e
contrattare sul prezzo di scambio dovrebbe modificare di poco gli equilibri finali rispetto ad una situazione di concorrenza perfetta. Per prevedere quantità e prezzi di equilibrio su questi mercati quasi-concorrenziali, il modello standard di domanda ed offerta
appare perciò uno strumento appropriato.
5. Il nostro esperimento reale
Vogliamo verificare quanto raccontato fin qui effettuando un esperimento reale, che è
molto simile a quello realizzato da Smith, tranne per il fatto che utilizzeremo tastiere e
computer anziché biglietti di carta e lavagne.
In aula informatica sarete divisi in due gruppi: compratori e venditori. A ciascun compratore sarà assegnato un numero che lo identificherà (ad esempio, compratore n. 31);
anche a ciascun venditore sarà assegnato un numero identificativo (ad esempio, venditore n. 6).
Ad ognuno verrà poi assegnato un prezzo massimo di acquisto (se compratore) o un
prezzo minimo di vendita (se venditore) per una unità di un generico bene X. Ciascun
compratore potrà contattare tramite il suo computer un qualunque venditore indicandone
il numero e digitando un prezzo a cui è disposto a comprare il bene da lui. Specularmente, ciascun venditore potrà contattare tramite il suo computer un qualunque compratore
indicandone il numero e digitando un prezzo a cui è disposto a vendergli il bene.
Ogni compratore può contattare un solo venditore alla volta, ed ogni venditore può contattare un solo compratore alla volta.4 Comunque, le proposte di acquisto e di vendita
possono essere ritirate in ogni momento per farne di nuove ai soggetti già contattati o a
diversi soggetti. Inoltre, ogni compratore può essere contattato in qualsiasi momento da
diversi venditori disposti a vendergli il bene, magari ognuno ad un prezzo diverso. Specularmente, ogni venditore può essere contattato in qualsiasi momento da diversi compratori disposti ad acquistare il bene da lui, probabilmente a prezzi diversi.
Un contratto si chiude nel momento in cui un compratore accetta la proposta ricevuta da
uno specifico venditore, oppure quando un venditore accetta la proposta a lui pervenuta
4
Questa è una prima differenza importante tra il nostro esperimento e quello di Smith, nel quale invece
ogni proposta di acquisto o di vendita veniva effettuata pubblicamente.
8
da uno specifico compratore.
Quando un contratto si chiude (ad esempio tra il compratore n. 31 e il venditore n. 6 per
un prezzo pari a 10 €), tutti gli agenti sul mercato vedranno apparire sul proprio schermo un avviso del tipo: “Il compratore n. 31 e il venditore n. 6 hanno scambiato l’unità
del bene a 10 €”.5
Le contrattazioni possono andare avanti per un certo numero di minuti, dopodiché il
mercato si chiude. Chi ha comprato/venduto il bene avrà realizzato un certo surplus: per
i compratori questo surplus è dato dalla differenza tra il loro prezzo massimo di acquisto
e il prezzo effettivamente pagato; per i venditori il surplus è dato dalla differenza tra il
prezzo di vendita effettiva e il loro prezzo minimo di vendita. Per chi non ha comprato/venduto il bene, il surplus è uguale a zero.
Vi sono diversi periodi di contrattazione. L’esperimento viene cioè ripetuto per più di
una volta, come se ci fossero più giorni di mercato. I surplus realizzati da ciascun agente
nei diversi periodi di contrattazione vengono sommati.
“Vince” il gioco chi ottiene un surplus totale più elevato.
Da un punto di vista economico, ci interesserà vedere:
1) se col susseguirsi dei giorni di mercato la quantità totale scambiata sul mercato si
avvicina a quella di equilibrio, calcolata con le curve di domanda e di offerta teoriche;
2) se il prezzo medio a cui il bene è scambiato si avvicina al prezzo di equilibrio, calcolato con le curve di domanda ed offerta teoriche;
3) se la variabilità dei prezzi a cui avvengono gli scambi diminuisce nel tempo, in modo tale che i prezzi di compravendita tendono ad essere sempre più vicini al prezzo
medio man mano che si susseguono i giorni di mercato.
5
Nell’esperimento di Smith, alla chiusura di ogni contratto oltre al prezzo di compravendita del bene venivano resi pubblici anche il prezzo massimo di acquisto del compratore e il prezzo minimo di vendita del
venditore. Questa è un’altra differenza rilevante tra il nostro esperimento e quello di Smith.
9












