Politecnico di Torino
CeTeM
Elettronica applicata
-
Elettronica
applicata
Prev
Home
Next
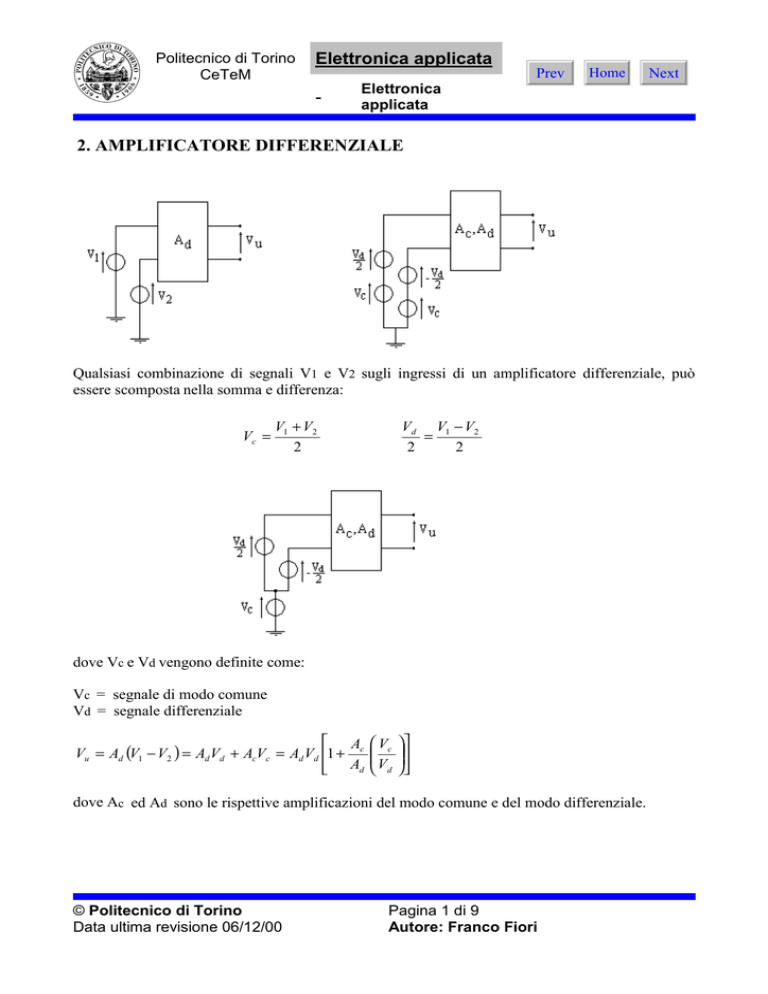
2. AMPLIFICATORE DIFFERENZIALE
Qualsiasi combinazione di segnali V1 e V2 sugli ingressi di un amplificatore differenziale, può
essere scomposta nella somma e differenza:
Vc =
V1 + V2
2
Vd V1 − V2
=
2
2
dove Vc e Vd vengono definite come:
Vc = segnale di modo comune
Vd = segnale differenziale
A V
Vu = Ad (V1 − V2 ) = Ad Vd + AcVc = Ad Vd 1 + c c
Ad Vd
dove Ac ed Ad sono le rispettive amplificazioni del modo comune e del modo differenziale.
© Politecnico di Torino
Data ultima revisione 06/12/00
Pagina 1 di 9
Autore: Franco Fiori
Elettronica applicata
Politecnico di Torino
CeTeM
Prev
Elettronica
applicata
-
Home
Next
L’amplificatore differenziale è lo stadio di ingresso di un amplificatore operazionale il cui schema
generale (ad accoppiamento di emettitore con transistori BJT) è indicato in figura:
La Io impressa dal generatore di corrente viene ripartita fra i due transistori Q1 e Q2 in funzione di
Vd.
- corrente di emettitore per Q1:
V
I E1 = I S 1 ⋅ exp BE1
VT 1
I S1 ∝ AE1
VT 1 =
KT1
q
VT 2 =
KT2
q
- corrente di emettitore per Q2:
V
I E 2 = I S 2 ⋅ exp BE 2
VT 2
I S 2 ∝ AE 2
dove: A= area dell’emettitore
T= temperatura in gradi Kelvin
K= costante di Boltzmann
q = carica dell’elettrone
Se Q1 = Q2 ovvero considerando i due transistori accoppiati identici (matched) ed operanti alla
stessa temperatura (T1=T2), allora:
I S1 = I S 2 = I S
VT 1 = VT 2 = VT ≅ 26 mV a 25°C
In generale possiamo dire che:
I E1 + I E 2 = I 0
I E1
I E2
V
I S ⋅ exp BE1
VT = exp Vd
=
V
VBE 2
T
I S ⋅ exp
VT
© Politecnico di Torino
Data ultima revisione 06/12/00
infatti :
Pagina 2 di 9
Autore: Franco Fiori
VBE1 − VBE 2 = Vd
Politecnico di Torino
CeTeM
Elettronica applicata
-
Elettronica
applicata
Prev
Home
Next
da cui si possono ricavare le seguenti relazioni che legano le correnti di emettitore dei due
transistori Q1 e Q2 alla tensione Vd :
V
I 0 exp d
I0
VT
I E2 =
I E1 =
V
V
1 + exp d
1 + exp d
VT
VT
Il grafico seguente mostra l’andamento delle correnti di emettitore in funzione del valore di Vd.
Per valori di Vd compresi fra –VT e +VT i transistori lavorano in regione lineare.
La pendenza della trascaratteristica viene definita “transconduttanza” dell’amplificatore:
gm =
dI C
dI
≅ E
dVd dVd
© Politecnico di Torino
Data ultima revisione 06/12/00
per α ≅ 1
I
g m è massima per I E = 0
2
Pagina 3 di 9
Autore: Franco Fiori
Politecnico di Torino
CeTeM
Elettronica applicata
Prev
Elettronica
applicata
-
Home
Next
Guadagno di modo differenziale
Per il calcolo del guadagno di modo differenziale, viene considerata nulla la componente di modo
comune Vc della tensione di segnale, valutando solamente gli effetti delle componenti differenziali
+Vd/2 e –Vd/2.
Il guadagno Ad del modo differenziale è dato dall’espressione:
Ad =
Vu
Vd
dove:
Ad 1 =
Vu1
;
Vd
Vu1 = − RC g m1
Ad 2 =
Vu 2
;
Vd
Vd
2
Vu = Vu1 − Vu 2
Ad 1 = − Ad 2
g m1 =
I C1
I
= o
VT
2VT
⇒
Vu1 = − RC
I o Vd
2VT 2
I calcoli possono quindi essere effettuati per l’altro stadio.
Determiniamo infine i guadagni Ad1, Ad2 ed il guadagno totale Ad dell’amplificatore differenziale:
Ad 1 =
Vu1
I
1
= − RC o = − g m RC
Vd
4VT
2
⇒ Ad = − RC
Io
= − g m RC
2VT
Vu 2
I
1
= RC o = g m RC
Vd
4V
2
Le espressioni
di Ad1T e di Ad2 sono i guadagni di modo differenziale dell’amplificatore prendendo
l’uscita in modo single-ended, cioè in modo “sbilanciato” (uscita presa tra un collettore e la massa,
anzichè in modo differenziale).
La resistenza di ingresso, per il modo differenziale, è data dall’espressione:
Ad 2 =
Rid = 4hfe
VT
hfe
=2
= 2hie
I0
gm
Guadagno di modo comune
© Politecnico di Torino
Data ultima revisione 06/12/00
Pagina 4 di 9
Autore: Franco Fiori
Politecnico di Torino
CeTeM
Elettronica applicata
-
Elettronica
applicata
Prev
Home
Next
Per valutare il guadagno di modo comune, vengono considerate nulle le componenti differenziali
della tensione di segnale (+Vd/2 e –Vd/2) tenendo conto solamente della tensione di modo comune
Vc.
Come si può notare dallo schema circuitale viene ora considerata anche la resistenza Ro
caratteristica del generatore di corrente Io. Per facilitare i calcoli consideriamo tale generatore come
il risultato della somma degli effetti di due generatori di corrente (Io/2) :
Nell’ipotesi di perfetta simmetria dei due circuiti accoppiati, il guadagno di modo comune
dell’amplificatore (prendendo l’uscita single ended) è uguale a:
αR
Vu1 Vu 2
R
=
=− C ≅− C
Vc
Vc
2 R0
2 R0
Considerando la corrente d’ingresso ib, la resistenza d’ingresso, per il modo comune sarà:
Ac =
Vc
≅ hie + R0 (1 + hfe) ≅ R0 (1 + hfe)
ib
La resistenza d’ingresso così definita è la resistenza che si vede guardando nei due ingressi connessi
insieme, ed è elevata.
Ric =
Si osserva che per valori crescenti di Ro, il guadagno di modo comune diminuisce.
© Politecnico di Torino
Data ultima revisione 06/12/00
Pagina 5 di 9
Autore: Franco Fiori
Politecnico di Torino
CeTeM
Elettronica applicata
Elettronica
applicata
-
Prev
Home
Next
Inoltre, anche in presenza di Ro, la tensione di uscita Vu non risente dell’amplificazione di modo
comune, proprietà fondamentale per un amplificatore differenziale ideale.
Rapporto di reiezione al modo comune
Per avere un’ indicazione della reiezione al modo comune da parte dell’amplificatore differenziale,
viene definito il CMRR (Common Mode Rejection Ratio):
CMRR =
Ad
≈ g m R0
Ac
(CMRR) dB = 20 log
Ad
= 20 log Ad − 20 log Ac
Ac
In generale il calcolo del CMMR avviene calcolando i guadagni di modo comune e differenziale
prendendo l’uscita single-ended dell’amplificatore, in quanto per un amplificatore differenziale
ideale, il guadagno di modo comune, prendendo l’uscita in modo differenziale è Ac =0.
Dinamica di ingresso e di uscita di modo comune e differenziale
DEFINIZIONI
Dinamica d’ingresso per il modo differenziale
E’ il campo di valori di tensione nel quale può variare un segnale di ingresso differenziale
applicato agli ingressi senza che intervengano fenomeni di non linearità dell’amplificatore.
Dinamica d’uscita per il modo differenziale
E’ il campo di valori all’uscita dell’amplificatore, quando il segnale di modo differenziale è
all’interno della dinamica d’ingresso.
Dinamica d’ingresso per il modo comune
E’ il campo di valori di tensione nel quale può variare un segnale di modo comune applicato
agli ingressi senza che intervengano fenomeni di non linearità dell’amplificatore.
Dinamica d’uscita per il modo comune
E’ il campo di valori all’uscita dell’amplificatore, quando il segnale di modo comune è
all’interno della dinamica d’ingresso. L’amplificatore differenziale ideale ha in uscita la
tensione Vu =0 per quanto riguarda l’amplificazione del solo modo comune.
© Politecnico di Torino
Data ultima revisione 06/12/00
Pagina 6 di 9
Autore: Franco Fiori
Politecnico di Torino
CeTeM
Elettronica applicata
-
Elettronica
applicata
Prev
Home
Next
SPECCHIO DI CORRENTE
Il generatore di corrente Io, visto nei circuiti finora analizzati, può essere realizzato attraverso un
particolare circuito detto “specchio di corrente” riportato in figura:
Il transistore Q1 è connesso a diodo, ed essendo percorso dalla corrente Io, ai suoi capi si crea una
differenza di potenziale pari a circa 0,6 – 0,7 Volt.
Essendo le basi dei due transistori collegate insieme, così come i rispettivi emettitori, tale VBE è la
stessa del transistore Q2 che presenterà quindi anch’esso una corrente di collettore pari ad Io.
Lo specchio di corrente (se i due transistori sono identici : condizione che a causa delle tolleranze
dei componenti è solamente ideale) funziona in maniera ottimale e sia il lato debole che quello forte
sono percorsi dal medesimo valore di corrente.
Si dice lato debole quello il cui valore di corrente dipende in maniera sensibile dai valori dei
componenti di quel lato (p.e. valore della resistenza R e dell’alimentazione VAL).
Si dice altresì lato forte quel lato il cui valore di corrente dipende, in generale, unicamente dalla
corrente imposta.
© Politecnico di Torino
Data ultima revisione 06/12/00
Pagina 7 di 9
Autore: Franco Fiori
Politecnico di Torino
CeTeM
Elettronica applicata
-
Elettronica
applicata
Prev
Home
Next
ESERCIZI
Esercizio n°1
Del circuito rappresentato in figura, determinare la tensione differenziale in ingresso affinchè
Ie1=0,98 Io considerando una temperatura di 25°C.
Soluzione:
Ricordando che:
I0
I e1 =
V − V1
1 + exp 2
V
T
Vd = V1 − V2
l’incognita di questa espressione è il segnale differenziale:
V − V1
1
V −V
= 0,0204 ⇒ 2 −13 = ln (0,0204 ) ⇒ Vd = 97 mV
= 0,98 ⇒ exp 2
V − V1
25 ⋅ 10
VT
1 + exp 2
VT
Si può quindi dimostrare che per valori di Vd ≈ 4VT la corrente di emettitore del transistore è
uguale in pratica alla corrente del generatore Io.
Esercizio n°2
Determinare il CMRR in dB di un amplificatore differenziale con ingresso a BJT ad accoppiamento
di emettitore con Ad=100, che presenta una tensione in uscita Vu=1,8 V applicando in ingresso i
segnali:
V1=220 mV e V2=200 mV
© Politecnico di Torino
Data ultima revisione 06/12/00
Pagina 8 di 9
Autore: Franco Fiori
Politecnico di Torino
CeTeM
Elettronica applicata
-
Elettronica
applicata
Prev
Soluzione
Per calcolare l’amplificazione di modo comune Ac:
V + V2
Vu = Ad Vd + AcVc = Ad (V1 − V2 ) + Ac ⋅ 1
= 2,0 + Ac ⋅ 0,210 = 1,8 V
2
0,2
⇒ Ac =
= 0,952
0,210
per cui:
(CMRR) dB = 20 log
Ad
100
= 20 log
≅ 40 dB
Ac
0,952
© Politecnico di Torino
Data ultima revisione 06/12/00
Pagina 9 di 9
Autore: Franco Fiori
Home
Next










