Applicazione dei limiti alla geometria piana
Problema di geometria sui limiti
. Condurre per il vertice A una semiretta
Nel triangolo ABC, con AB = c , è noto che B AC = 3 ABC
siano congruenti.
s che intersechi il lato BC in P in modo che gli angoli B AP , PBA
AP
tende a zero e quando tende a π .
Q1- Calcolare il limite del rapporto
quando l’angolo PBA
4
AC
BH
Q2- Indicata con H la proiezione di B sulla semiretta s, calcolare i limiti del rapporto
quando
PB
tende a zero e quando tende a π .
l’angolo PBA
4
Guida alla soluzione
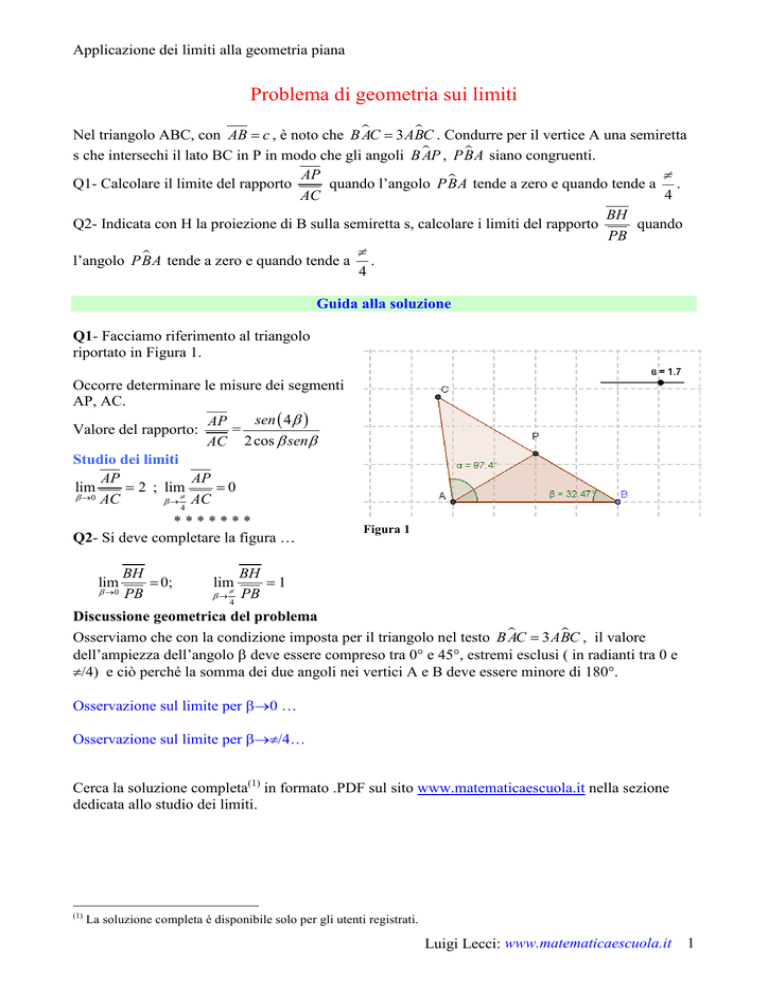
Q1- Facciamo riferimento al triangolo
riportato in Figura 1.
Occorre determinare le misure dei segmenti
AP, AC.
sen ( 4β )
AP
Valore del rapporto:
=
AC 2 cos β senβ
Studio dei limiti
AP
AP
lim
= 2 ; lim
=0
π
β → 0 AC
β → AC
4
*******
Q2- Si deve completare la figura …
BH
= 0;
β → 0 PB
lim
lim
β→
π
4
Figura 1
BH
=1
PB
Discussione geometrica del problema
, il valore
Osserviamo che con la condizione imposta per il triangolo nel testo B AC = 3 ABC
dell’ampiezza dell’angolo β deve essere compreso tra 0° e 45°, estremi esclusi ( in radianti tra 0 e
π/4) e ciò perché la somma dei due angoli nei vertici A e B deve essere minore di 180°.
Osservazione sul limite per β→0 …
Osservazione sul limite per β→π/4…
Cerca la soluzione completa(1) in formato .PDF sul sito www.matematicaescuola.it nella sezione
dedicata allo studio dei limiti.
(1)
La soluzione completa è disponibile solo per gli utenti registrati.
Luigi Lecci: www.matematicaescuola.it
1












