Limiti da problemi sul triangolo isoscele

Verso l’Esame di Stato nel Liceo Scientifico
Limiti da problemi sul triangolo isoscele
(un triangolo isoscele con angolo di 120°)
Problema
Sia ABC un triangolo isoscele con l’angolo nel vertice A di ampiezza 120° e i cui lati congruenti misurano 2a.
Si consideri sulla base BC un punto P e indicata con x la misura del segmento BP si studi il seguente limite
lim
PB
AB  AP
.
BP
Risposta:
3
2
Elaborazioni
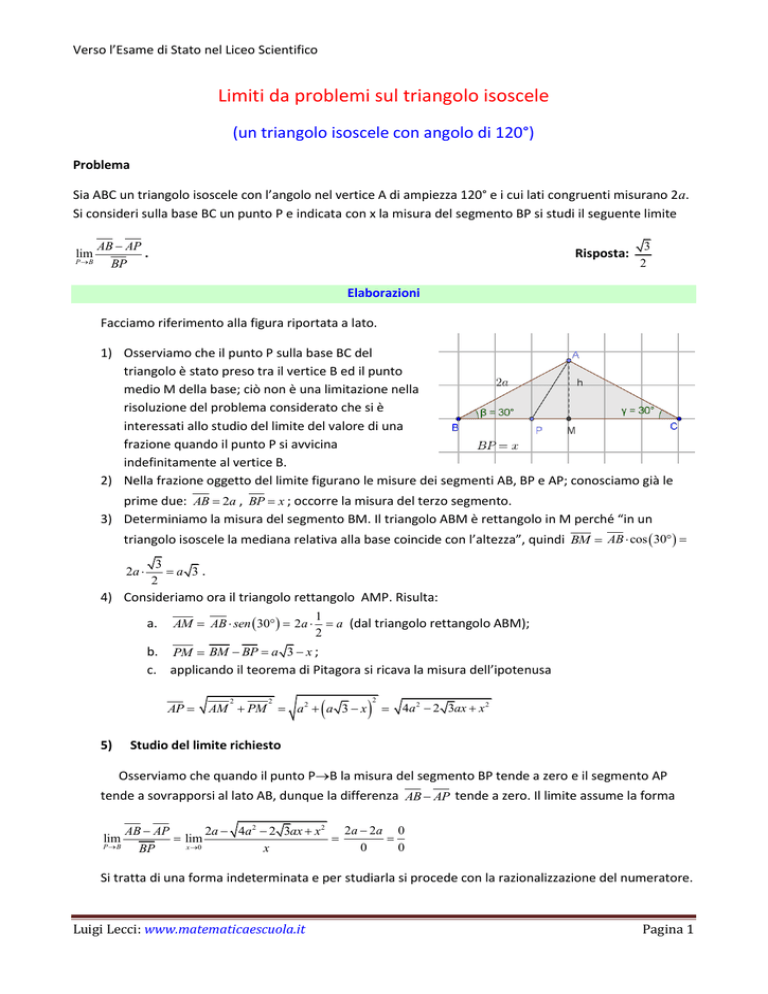
Facciamo riferimento alla figura riportata a lato.
1) Osserviamo che il punto P sulla base BC del
triangolo è stato preso tra il vertice B ed il punto
medio M della base; ciò non è una limitazione nella
risoluzione del problema considerato che si è
interessati allo studio del limite del valore di una
frazione quando il punto P si avvicina
indefinitamente al vertice B.
2) Nella frazione oggetto del limite figurano le misure dei segmenti AB, BP e AP; conosciamo già le
prime due: AB  2a , BP  x ; occorre la misura del terzo segmento.
3) Determiniamo la misura del segmento BM. Il triangolo ABM è rettangolo in M perché “in un
triangolo isoscele la mediana relativa alla base coincide con l’altezza”, quindi BM  AB  cos  30  
2a 
3
a 3.
2
4) Consideriamo ora il triangolo rettangolo AMP. Risulta:
a.
AM  AB  sen  30   2a 
1
 a (dal triangolo rettangolo ABM);
2
b. PM  BM  BP  a 3  x ;
c. applicando il teorema di Pitagora si ricava la misura dell’ipotenusa
AP 
5)
2
2

AM  PM  a 2  a 3  x

2

4a 2  2 3ax  x 2
Studio del limite richiesto
Osserviamo che quando il punto PB la misura del segmento BP tende a zero e il segmento AP
tende a sovrapporsi al lato AB, dunque la differenza AB  AP tende a zero. Il limite assume la forma
lim
PB
2a  2a 0
AB  AP
2a  4a 2  2 3ax  x 2

 lim

x

0
0
0
x
BP
Si tratta di una forma indeterminata e per studiarla si procede con la razionalizzazione del numeratore.
Luigi Lecci: www.matematicaescuola.it
Pagina 1
Verso l’Esame di Stato nel Liceo Scientifico
2a  4a  2 3ax  x 2a  4a  2 3ax  x

 lim
x 0
x
2a  4a 2  2 3ax  x 2
2
lim
x 0
lim
x 0
2
1
2a  4a 2  2 3ax  x 2
2
2
 2a 
2


4a 2  2 3ax  x 2
x


2

x 2 3a  x
1
2 3ax  x 2 1
1
3
 lim



 2 3a 
x

0
x 0
x
4 a 4a
4a
2
x
 lim
Luigi Lecci: www.matematicaescuola.it
Pagina 2