Relatività speciale -Trasformazioni di Lorentz
ESEMPI DI INVARIANTI DI LORENTZ
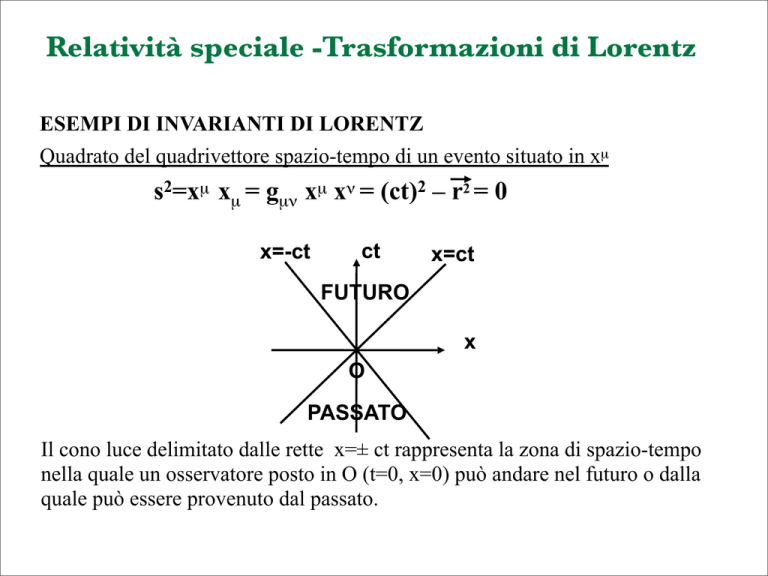
Quadrato del quadrivettore spazio-tempo di un evento situato in xµ
s2=xµ xµ = gµν xµ xν = (ct)2 – r2 = 0
x=-ct
ct
x=ct
FUTURO
x
O
PASSATO
Il cono luce delimitato dalle rette x=± ct rappresenta la zona di spazio-tempo
nella quale un osservatore posto in O (t=0, x=0) può andare nel futuro o dalla
quale può essere provenuto dal passato.
Consideriamo la distanza al quadrato tra due eventi nello spazio tempo x1µ e x2µ
s122= c2 (t1 – t2)2 – ( r1 – r2 )2
Se ( r1 – r2 )2 = c2 (t1 – t2)2 ciò significa che i due punti possono essere collegati
da un segnale che si propaga alla velocità della luce, cioè tra di essi vi può essere
una relazione di causa-effetto.
Se i due punti distano in modo tale che: ( r1 – r2 )2 > c2 (t1 – t2)2 ciò significa che
i due punti non potranno mai essere collegati da un segnale, perchè questo
dovrebbe propagarsi a velocità superiore a quella della luce, cioè tra di essi non
vi potrà mai essere una relazione di causa-effetto.
Se i due punti distano in modo tale che: ( r1 – r2 )2 < c2 (t1 – t2)2 ciò significa che
i due punti possono essere collegati da un segnale che si propaga a velocità
inferiore a quella della luce, cioè tra di essi vi potrà essere una relazione di
causa-effetto.
Essendo s12 uno scalare e quindi un invariante, il segno di tale quantità sarà lo
stesso in tutti i sistemi di riferimento e pertanto, se due eventi sono in relazione
di causa-effetto in un sistema essi lo saranno anche in tutti gli altri.
Relatività speciale - Cinematica
SISTEMA DI RIFERIMENTO DEL LABORATORIO
È il sistema nel quale la particella bersaglio (2 ad es.) è a riposo e la particella
proiettile è in movimento (1 ad es.):
Supponiamo di avere solo due particelle uscenti (3 e 4). I loro quadrimpulsi:
dovranno soddisfare alle relazioni:
E
E
E
Relatività speciale - Cinematica (continua)
SISTEMA DI RIFERIMENTO DEL CENTRO DI MASSA
È il sistema nel quale le particelle iniziali (e quindi anche finali) hanno impulso
totale nullo. Pertanto le due particelle iniziali hanno tri-impulsi uguali in modulo
e direzione e opposti in verso:
Le loro energie saranno invece diverse:
E
E
Le due particelle uscenti 3 e 4 dovranno avere quadrimpulsi ed energie:
E
che soddisfano alla seguente relazione:
E
Relatività speciale - Cinematica (continua)
INVARIANTI CINEMATICI
Per ovviare al problema dovuto al fatto che in ogni sistema di riferimento i
quadrimpulsi e le relazioni cinematiche tra essi sono differenti, si possono
introdurre delle quantità invarianti, che hanno lo stesso valore in ogni sistema.
Prendiamo la reazione 1+2→ 3+4
p1
1
3
p3
p2
2
4
p4
Relatività speciale - Cinematica (continua)
INVARIANTI CINEMATICI (continua) - VARIABILI DI MANDELSTAM
Le seguenti quantità sono invarianti cinematici (uguali in ogni S.R.):
s = ( p1 + p2)2 = ( p3 + p4)2
t = ( p1 - p3)2 = ( p2 - p4)2
VARIABILI DI MANDELSTAM
u = ( p1 - p4)2 = ( p2 - p3)2
p3
p1
p2
¬
√s
p1
p3
¬
√t
p4
p2
p4
p3
p1
p2
¬
√u
p4
Relatività speciale - Cinematica (continua)
INVARIANTI CINEMATICI (continua) - VARIABILI DI MANDELSTAM
Nel sistema del CM avremo:
s = ( p1* + p2*)2 =
⇒ ENERGIA TOTALE NEL C.M.
= (E1* + E2*)2 - ( p* - p*)2 = (E1* + E2*)2
s = ( p3* + p4*)2 = (E3* + E4*)2
Solo due di essi sono linearmente indipendenti in quanto essi sono legati dalla
relazione:
s+t+u
= (p1 + p2)2 + (p1 - p3)2 + (p1 + p4)2 =
= p1 2 + p2 2 + 2 p1 p2 + p1 2 + p3 2 - 2 p1 p3 + p1 2 + p4 2 - 2 p1 p4 =
= (p1 2 + p2 2 + p3 2 + p4 2) + 2 ( p1 ( p1 + p2 ) - p1 ( p3 + p4 )) =
ma: p1 + p2 = p3 + p4 ⇒ s + t + u
= m12+m22+m32+m42
Relatività speciale- La dilatazione dei tempi
Come conseguenza delle trasformate di Lorentz si ha il fatto che gli intervalli di
tempo cambiano da un sistema di riferimento all’altro.
Questo è particolarmente evidente nel decadimento di una particella in volo. Se τ
la sua vita media quando essa è a riposo, quando si muove di velocità v decadrà
rispetto all’osservatore del laboratorio con una vita media τ’:
τ’ = γ τ
Poichè γ > 1, ciò significa che nel sistema in cui la particella si muove, essa
verrà vista decadere dopo un tempo maggiore rispetto alla sua vita media (cioè
al tempo di decadimento nel sistema in cui è a riposo).
Consideriamo ad esempio il muone che ha τ = 2.2 µs. Se esso
possiede un’energia di 50 GeV, la sua vita media misurata in laboratorio sarà:
τ’ = γ τ = τ E/ (mc2) = τ ×50 GeV/(0.106 GeV) =
= 500 τ = 1100 µs =1.1 ms
Due piccoli accorgimenti per fare dei calcoli:
1)
ħc = hc/(2π) = 1.055 10 -34 J s × 3 × 10 8 m s-1 =
~ 3. × 10 -26 J m
Come abbiamo visto prima:
1 eV = 1.602 × 10-19 J
=> 1 J = 1 eV / (1.602 × 10-19 ) = 0.624 × 1019 eV
Dunque:
ħc = 3. × 10 -26 J m = 3 × 10 -26 × 0.624 × 1019 eV m =
= 1.9 × 10 -7 eV m = 1.9 × 10 -7 × 10 -6 eV × 10 15 fm =
= 1.9 × 10 2 MeV fm ~ 200 MeV fm
N.B. 1fm = 10 -15 m
2) α = e2 / ħc = 1/137 (costante di struttura fine adimensionale)
=> e2 = ħc a = 200 MeV fm 1/137 = 1.44 MeV fm
Esempio:
Calcolare l’impulso di un pione avente un’energia cinetica di 200 MeV
T = E – m => E = T + m = 200 MeV + 135 MeV = 235 MeV
Calcolare l’energia cinetica di un protone avente un impulso di 5 MeV/c
E = [p2 + m2]½ = [ 5 MeV2 + (938.56 MeV)2]½ =
= [ 25. MeV2 + 88. × 104 MeV2 ]½ ~ 9.39 × 102 MeV
T = E – m = 9.39 × 102 MeV - 938.56 MeV =
= 0.0133 MeV = 1.33 × 10-2 MeV
N.B. Poichè (pc)<< mc2 possiamo anche applicare la formula classica:
T = p2 / 2m = (5 MeV)2 / (2 × 938.56 MeV) =
= 25. MeV2/(1.877 × 103 MeV) = 1.33 × 10-2 MeV
Decadimento del π0
y
y
(SL)
(SR)
x
x
γ1
θ
γ2
z=z
Decadimento del π0
ossia:
Poiché m γ = 0
Applicando le
trasformazioni:
Decadimento del π0
Maggiore è l’energia del γ emesso in avanti
Gli angoli di emissione nel laboratorio
rispetto alla direzione del π0 sono diversi:
L’angolo α tra i due γ nel SL (detto angolo di
apertura):
Decadimento del π0
l'angolo minimo: αmin si ha per
L’angolo di apertura minimo 0 quando β 1
ACCELERAZIONE DI PARTICELLE
È necessario portare le particelle a energie elevate per varie ragioni:
• Aumentare il potere risolutivo della particella che funge da sonda
( vedi trasparenze precedenti)
• Produrre particelle finali nuove e di massa elevata
A+B→C
Gli esperimenti che si realizzano possono essere:
- a bersaglio fisso
- a fasci collidenti
Vediamo ora che differenza c’è tra le energie totali sviluppate nel C.M. nei due
casi e le conseguenze che essa ha sull’energia di soglia per la produzione di
particelle finali.
ESPERIMENTO A BERSAGLIO FISSO A+B → C
Sistema del LAB:
Sistema del C.M.:
La quantità che si conserva tra i due sistemi è il quadrato del 4-impulso pc, che
ci fornisce la massa della particella C prodotta e il quadrato dell’energia totale
nel C.M.:
Come si vede dalla formula (54), l’energia totale nel C.M. dipende quindi dalla
radice quadrata dell’energia del fascio incidente:
Energia di soglia per la creazione di una particella di massa mC:
Dato che (dalla formula (54)):
se vogliamo creare una particella di massa mC sarà dunque necessario un fascio
di energia minima (energia di soglia, “threshold” in inglese):
Nel caso particolare di particelle ultrarelativistiche, per le quali possiamo
trascurare la massa rispetto all’energia, l’energia nel centro di massa nel caso di
bersaglio fisso sarà data semplicemente da:
ESPERIMENTO A FASCI COLLIDENTI A+B → C
Sistema del LAB:
Sistema del C.M.:
Come prima, la quantità che si conserva tra i due sistemi è il quadrato del 4impulso pc, che è uguale alla massa della particella C prodotta e al quadrato
dell’energia totale nel C.M.:
Come si vede dalla formula (57), l’energia totale nel C.M. dipende quindi
dalla radice quadrata del prodotto delle energie dei fasci collidenti:
Mettiamoci ora nel caso più semplice di due fasci di particelle di uguale massa
mA=mB=m, impulsi uguali e opposti (θ12=180° → cos θ12= -1). La (57) in tal
caso diventa:
Come si vede dalla (59) l’energia totale nel C.M. è pari alla somma delle
energie dei due fasci collidenti, cioè varia linearmente con l’energia (ricordiamo
che invece nel caso di bersaglio fisso, essa varia come la radice quadrata
dell’energia del proiettile).
Energia di soglia per la creazione di una particella di massa mC:
Dato che (dalla formula (59)):
se vogliamo creare una particella di massa mC sarà necessario un fascio di
energia minima pari a:
1) Calcolare l’energia totale di un pione avente un’energia cinetica di 200 MeV:
2) Calcolare l’energia cinetica di un protone avente un impulso di 5 MeV/c:
Soluzione:
Dato che il protone non è relativistico (infatti p<<m), possiamo anche
applicare la formula classica dell’energia cinetica che ci deve fornire lo stesso
risultato:
3) Calcolare l’impulso di un kaone avente energia cinetica 1GeV
(mK = 493.6 MeV/c2)
Soluzione:
4) Calcolare l’energia totale di un protone avente impulso p=300 MeV/c
(N.B. mp =938. MeV/c2)
Soluzione:
5) Due particelle, entrambe di massa m, collidono testa a testa con velocità
entrambe uguali a (3/5)c e si uniscono a formare una particella unica di massa
M. Qual è la massa M della particella finale?
Soluzione:
m
M
m
Per ricavare E in funzione della velocità delle due particelle, ricordiamo che:
Notiamo che la massa della particella finale è superiore alla semplice somma
delle masse delle due particelle iniziali. Ciò è possibile perchè l’energia
cinetica delle due particelle iniziali si è trasformata in massa.
6) Una particella di massa M, a riposo, decade in due particelle di massa uguale
m. A quale velocità si muoveranno le due particelle finali?
Soluzione:
m
M
m
Per estrarre le velocità delle due particelle, nuovamente esprimiamo E come:
La radice quadrata deve avere radicando positico e quindi occorre che sia:
Questo significa che, perchè il decadimento della particella di massa M nelle
due particelle di massa m possa avvenire, occorre che la particella iniziale
abbia almeno una energia a riposo (cioè una massa) pari alle masse delle due
particelle finali. L’eventuale eccedenza tra M e 2m sarà trasformata in energia
cinetica.
L’energia di soglia per il decadimento è quindi:
7) Un pione a riposo decade in un muone e un neutrino. Qual è la velocità del
muone?
Soluzione:
Sostituendo la (3) e la (4) nella (1) otteniamo:
mµ
mπ
mν
Per ottenere la velocità del muone (o il suo βµ il che è lo stesso), ricordiamo
la relazione che lega βµ all’impulso e all’energia della particella:
Dove pµ è dato dalla (5) e Eµ è dato da:
8) Nel Bevatron di Berkeley un fascio di protoni incidendo su un bersaglio
anch’esso di protoni, produceva antiprotoni attraverso la seguente reazione:
Qual è l’energia di soglia che deve avere il fascio incidente perchè la reazione
(1) abbia luogo?
Soluzione:
LAB: Stato iniziale
LAB: Stato finale
CM: Stato iniziale
CM: Stato finale
Per ricavare la condizione per l’energia di soglia, notiamo che nel C.M. in
corrispondenza di tale energia le particelle dello stato finale vengono prodotte
a riposo:
Consideriamo ora il quadrato del 4-impulso totale nel LAB prima dell’urto e
nel C.M. dopo l’urto (al posto di Ep sostituiamo la notazione Epth (per l’energia
di soglia nel laboratorio):
LAB prima dell’urto (caso in soglia):
CM dopo l’urto (caso in soglia):
I due quadrati del quadrimpulso prima e dopo l’urto, nel LAB e nel C.M.
devono comunque essere uguali tra loro. Pertanto possiamo uguagliare la (1) e
la (2) ed estrarre cosi l’energia di soglia (cioè l’energia minima che deve avere
il fascio nel laboratorio) per poter produrre tre protoni e un antiprotone:
9) Qual è la vita media di un pione π+ con un impulso di 100 GeV/c nel LAB?
dove:
10) A che velocità l’energia cinetica di una particella uguaglia la sua energia
di riposo?
Uguagliandole avremo:
5) vale il principio di indeterminazione di Heisenberg per la posizione e la
quantità di moto di una particella: quanto maggiore è la precisione nella
determinazione di una delle due variabili, tanto minore è quella nella
determinazione dell’altra:
5) vale il principio di indeterminazione di Heisenberg per la posizione e la
quantità di moto di una particella: quanto maggiore è la precisione nella
determinazione di una delle due variabili, tanto minore è quella nella
determinazione dell’altra:
5) vale il principio di indeterminazione di Heisenberg per la posizione e la
quantità di moto di una particella: quanto maggiore è la precisione nella
determinazione di una delle due variabili, tanto minore è quella nella
determinazione dell’altra:
Il principio vale anche nel mondo macroscopico, ma in pratica il piccolo valore
della costante di Planck fa sì che tale limitazione non abbia effetto (v.dopo).
5) vale il principio di indeterminazione di Heisenberg per la posizione e la
quantità di moto di una particella: quanto maggiore è la precisione nella
determinazione di una delle due variabili, tanto minore è quella nella
determinazione dell’altra:
Il principio vale anche nel mondo macroscopico, ma in pratica il piccolo valore
della costante di Planck fa sì che tale limitazione non abbia effetto (v.dopo).
5) vale il principio di indeterminazione di Heisenberg per la posizione e la
quantità di moto di una particella: quanto maggiore è la precisione nella
determinazione di una delle due variabili, tanto minore è quella nella
determinazione dell’altra:
Il principio vale anche nel mondo macroscopico, ma in pratica il piccolo valore
della costante di Planck fa sì che tale limitazione non abbia effetto (v.dopo).
Più in generale, il principio di indeterminazione afferma che coppie di variabili
canonicamente coniugate non possono essere simultaneamente determinate
entrambe con la precisione voluta. Un esempio di variabili canonicamente
coniugate è la coppia “posizione-quantità di moto”. Un’altra è la coppia “energiatempo”:
5) vale il principio di indeterminazione di Heisenberg per la posizione e la
quantità di moto di una particella: quanto maggiore è la precisione nella
determinazione di una delle due variabili, tanto minore è quella nella
determinazione dell’altra:
Il principio vale anche nel mondo macroscopico, ma in pratica il piccolo valore
della costante di Planck fa sì che tale limitazione non abbia effetto (v.dopo).
Più in generale, il principio di indeterminazione afferma che coppie di variabili
canonicamente coniugate non possono essere simultaneamente determinate
entrambe con la precisione voluta. Un esempio di variabili canonicamente
coniugate è la coppia “posizione-quantità di moto”. Un’altra è la coppia “energiatempo”:
Questo significa che una misurazione di energia che abbia una precisione voluta
ΔE, richiede una durata di tempo dell’ordine almeno di Δt ≥h/ΔE. Se un sistema
ha una durata di vita dell’ordine di Δt, la sua energia sarà determinata con
un’incertezza dell’ordine almeno di ΔE ≥h/Δt.
MECCANICA QUANTISTICA (CENNI)
MECCANICA QUANTISTICA (CENNI)
Alla base della Meccanica Quantistica sono i seguenti principi:
MECCANICA QUANTISTICA (CENNI)
Alla base della Meccanica Quantistica sono i seguenti principi:
1) esistono quantità che possono assumere solo valori discreti (v. il momento
angolare e l’energia negli spettri atomici, l’energia trasportata dai fotoni nel
corpo nero e nell’effetto fotoelettrico, lo spin delle particelle);
MECCANICA QUANTISTICA (CENNI)
Alla base della Meccanica Quantistica sono i seguenti principi:
1) esistono quantità che possono assumere solo valori discreti (v. il momento
angolare e l’energia negli spettri atomici, l’energia trasportata dai fotoni nel
corpo nero e nell’effetto fotoelettrico, lo spin delle particelle);
2) la radiazione e.m. ha una doppia natura onda-corpuscolo (come dimostrato
dallo spettro di corpo nero e dall’effetto fotoelettrico e Compton). L’energia della
radiazione e.m. è portata da singoli quanti o fotoni di energia E e impulso p (e
lunghezza e numero d’onda λ e k):
MECCANICA QUANTISTICA (CENNI)
Alla base della Meccanica Quantistica sono i seguenti principi:
1) esistono quantità che possono assumere solo valori discreti (v. il momento
angolare e l’energia negli spettri atomici, l’energia trasportata dai fotoni nel
corpo nero e nell’effetto fotoelettrico, lo spin delle particelle);
2) la radiazione e.m. ha una doppia natura onda-corpuscolo (come dimostrato
dallo spettro di corpo nero e dall’effetto fotoelettrico e Compton). L’energia della
radiazione e.m. è portata da singoli quanti o fotoni di energia E e impulso p (e
lunghezza e numero d’onda λ e k):
I fotoni hanno massa a riposo nulla e viaggiano alla velocità c.
N.B. La costante di Planck è molto piccola e vale:
MECCANICA QUANTISTICA (CENNI)
Alla base della Meccanica Quantistica sono i seguenti principi:
1) esistono quantità che possono assumere solo valori discreti (v. il momento
angolare e l’energia negli spettri atomici, l’energia trasportata dai fotoni nel
corpo nero e nell’effetto fotoelettrico, lo spin delle particelle);
2) la radiazione e.m. ha una doppia natura onda-corpuscolo (come dimostrato
dallo spettro di corpo nero e dall’effetto fotoelettrico e Compton). L’energia della
radiazione e.m. è portata da singoli quanti o fotoni di energia E e impulso p (e
lunghezza e numero d’onda λ e k):
I fotoni hanno massa a riposo nulla e viaggiano alla velocità c.
N.B. La costante di Planck è molto piccola e vale:
N.B. Questa relazione vale anche per i corpi macroscopici, ma la costante di
Planck è talmente piccola che la loro lunghezza d’onda è estremamente ridotta (v.
dopo).
3) anche le particelle materiali hanno una doppia natura onda-corpuscolo, in
quanto ad ogni particella materiale di impulso p è associata un’onda di lunghezza
d’onda λ legata a p dalla relazione di de Broglie:
N.B. Questa relazione vale anche per i corpi macroscopici, ma la costante di
Planck è talmente piccola che la loro lunghezza d’onda è estremamente ridotta (v.
dopo).
3) anche le particelle materiali hanno una doppia natura onda-corpuscolo, in
quanto ad ogni particella materiale di impulso p è associata un’onda di lunghezza
d’onda λ legata a p dalla relazione di de Broglie:
N.B. Questa è la stessa relazione che lega lunghezza d’onda e impulso per un fotone:
N.B. Questa relazione vale anche per i corpi macroscopici, ma la costante di
Planck è talmente piccola che la loro lunghezza d’onda è estremamente ridotta (v.
dopo).
3) anche le particelle materiali hanno una doppia natura onda-corpuscolo, in
quanto ad ogni particella materiale di impulso p è associata un’onda di lunghezza
d’onda λ legata a p dalla relazione di de Broglie:
N.B. Questa è la stessa relazione che lega lunghezza d’onda e impulso per un fotone:
N.B. Questa relazione vale anche per i corpi macroscopici, ma la costante di
Planck è talmente piccola che la loro lunghezza d’onda è estremamente ridotta (v.
dopo).
4) la particella materiale viene descritta in termini di una “funzione d’onda”
ψ(x,t) che dipende dallo spazio e dal tempo (approccio di Schrödinger alla
meccanica quantistica), il cui modulo al quadrato fornisce la probabilità di
trovare la particella in un certo punto dello spazio ad un certo istante.
La lunghezza d’onda del corpo macroscopico è piccolissima, mentre quella di un
elettrone è dell’ordine di grandezza delle dimensioni atomiche. Il comportamento
ondulatorio di un elettrone può essere pertanto verificato con delle fenditure di
larghezza confrontabile con λ (esperimento di Davisson e Germer).
Perchè le proprietà ondulatorie non si vedono per i corpi macroscopici?
La lunghezza d’onda del corpo macroscopico è piccolissima, mentre quella di un
elettrone è dell’ordine di grandezza delle dimensioni atomiche. Il comportamento
ondulatorio di un elettrone può essere pertanto verificato con delle fenditure di
larghezza confrontabile con λ (esperimento di Davisson e Germer).
Perchè le proprietà ondulatorie non si vedono per i corpi macroscopici?
Consideriamo un corpo macroscopico di 1 kg che si muove ad una velocità piccola,
come 3.6 km/h = 1. m/s e consideriamo un elettrone che si muove ad una velocità
altissima, prossima a c. Calcoliamo nei due casi la lunghezza d’onda:
La lunghezza d’onda del corpo macroscopico è piccolissima, mentre quella di un
elettrone è dell’ordine di grandezza delle dimensioni atomiche. Il comportamento
ondulatorio di un elettrone può essere pertanto verificato con delle fenditure di
larghezza confrontabile con λ (esperimento di Davisson e Germer).
Perchè le proprietà ondulatorie non si vedono per i corpi macroscopici?
Consideriamo un corpo macroscopico di 1 kg che si muove ad una velocità piccola,
come 3.6 km/h = 1. m/s e consideriamo un elettrone che si muove ad una velocità
altissima, prossima a c. Calcoliamo nei due casi la lunghezza d’onda:
N.B. Sfrutteremo le formule (45) e (42):
La lunghezza d’onda del corpo macroscopico è piccolissima, mentre quella di un
elettrone è dell’ordine di grandezza delle dimensioni atomiche. Il comportamento
ondulatorio di un elettrone può essere pertanto verificato con delle fenditure di
larghezza confrontabile con λ (esperimento di Davisson e Germer).
Perchè le proprietà ondulatorie non si vedono per i corpi macroscopici?
Consideriamo un corpo macroscopico di 1 kg che si muove ad una velocità piccola,
come 3.6 km/h = 1. m/s e consideriamo un elettrone che si muove ad una velocità
altissima, prossima a c. Calcoliamo nei due casi la lunghezza d’onda:
N.B. Sfrutteremo le formule (45) e (42):
CORPO MACROSCOPICO
La lunghezza d’onda del corpo macroscopico è piccolissima, mentre quella di un
elettrone è dell’ordine di grandezza delle dimensioni atomiche. Il comportamento
ondulatorio di un elettrone può essere pertanto verificato con delle fenditure di
larghezza confrontabile con λ (esperimento di Davisson e Germer).
Perchè le proprietà ondulatorie non si vedono per i corpi macroscopici?
Consideriamo un corpo macroscopico di 1 kg che si muove ad una velocità piccola,
come 3.6 km/h = 1. m/s e consideriamo un elettrone che si muove ad una velocità
altissima, prossima a c. Calcoliamo nei due casi la lunghezza d’onda:
N.B. Sfrutteremo le formule (45) e (42):
CORPO MACROSCOPICO
La lunghezza d’onda del corpo macroscopico è piccolissima, mentre quella di un
elettrone è dell’ordine di grandezza delle dimensioni atomiche. Il comportamento
ondulatorio di un elettrone può essere pertanto verificato con delle fenditure di
larghezza confrontabile con λ (esperimento di Davisson e Germer).
Perchè le proprietà ondulatorie non si vedono per i corpi macroscopici?
Consideriamo un corpo macroscopico di 1 kg che si muove ad una velocità piccola,
come 3.6 km/h = 1. m/s e consideriamo un elettrone che si muove ad una velocità
altissima, prossima a c. Calcoliamo nei due casi la lunghezza d’onda:
N.B. Sfrutteremo le formule (45) e (42):
CORPO MACROSCOPICO
ELETTRONE
La lunghezza d’onda del corpo macroscopico è piccolissima, mentre quella di un
elettrone è dell’ordine di grandezza delle dimensioni atomiche. Il comportamento
ondulatorio di un elettrone può essere pertanto verificato con delle fenditure di
larghezza confrontabile con λ (esperimento di Davisson e Germer).
Se conosciamo ad esempio la posizione di una palla di diametro 0.2 m e massa 1.
kg con una precisione dell’ordine di 0.1 mm, in base al principio di
indeterminazione conosceremo il suo impulso con una precisione Δp superiore a:
Se conosciamo ad esempio la posizione di una palla di diametro 0.2 m e massa 1.
kg con una precisione dell’ordine di 0.1 mm, in base al principio di
indeterminazione conosceremo il suo impulso con una precisione Δp superiore a:
Se conosciamo ad esempio la posizione di una palla di diametro 0.2 m e massa 1.
kg con una precisione dell’ordine di 0.1 mm, in base al principio di
indeterminazione conosceremo il suo impulso con una precisione Δp superiore a:
e cioè determineremo la sua velocità con una precisione non inferiore a:
Se conosciamo ad esempio la posizione di una palla di diametro 0.2 m e massa 1.
kg con una precisione dell’ordine di 0.1 mm, in base al principio di
indeterminazione conosceremo il suo impulso con una precisione Δp superiore a:
e cioè determineremo la sua velocità con una precisione non inferiore a:
Se conosciamo ad esempio la posizione di una palla di diametro 0.2 m e massa 1.
kg con una precisione dell’ordine di 0.1 mm, in base al principio di
indeterminazione conosceremo il suo impulso con una precisione Δp superiore a:
e cioè determineremo la sua velocità con una precisione non inferiore a:
che è un valore estremamente piccolo, quindi possiamo dire che la velocità
può essere determinata con una precisione piccola a piacere.
Perchè il principio di indeterminazione di Heisenberg non influenza la precisione
nelle misure macroscopiche?
Se conosciamo ad esempio la posizione di una palla di diametro 0.2 m e massa 1.
kg con una precisione dell’ordine di 0.1 mm, in base al principio di
indeterminazione conosceremo il suo impulso con una precisione Δp superiore a:
e cioè determineremo la sua velocità con una precisione non inferiore a:
che è un valore estremamente piccolo, quindi possiamo dire che la velocità
può essere determinata con una precisione piccola a piacere.
⇒ ma questa indeterminazione è dello stesso ordine di grandezza o superiore
dell’impulso che vorremmo determinare. Quindi se vogliamo determinare con
precisione la posizione dell’elettrone, non possiamo determinare con precisione il
suo impulso e viceversa.
Se vogliamo invece determinare la posizione di un elettrone di impulso
dell’ordine di una decina di KeV, poichè (come abbiamo visto) esso è associabile
a lunghezze d’onda dell’ordine dell’Angstrom, potremo chiedere di determinare
la sua posizione con una precisione dell’ordine, ad esempio, del decimo di Å (0.1
Å= 0.1 10-10 m). In tal caso potremo determinare il suo impulso con una
precisione superiore a:
⇒ ma questa indeterminazione è dello stesso ordine di grandezza o superiore
dell’impulso che vorremmo determinare. Quindi se vogliamo determinare con
precisione la posizione dell’elettrone, non possiamo determinare con precisione il
suo impulso e viceversa.
RANGE DELLE INTERAZIONI - MASSA DEL MEDIATORE
E1
E1
e1
e1
ΔE
e2
E2
γ
e2
E2
La particella 1 di energia E1 emette un fotone di energia
ΔE (violando cosi il principio di conservazione della
energia) e rincula di Δp1 = -ΔE/c, la particella 2 lo assorbe
e rincula di Δp2 = ΔE/c. Il principio di conservazione
dell’energia può essere violato solo per un tempo
massimo Δt tale che valga il principio di indeterminazione
di Heisenberg:
Se r è lo spazio percorso dal mediatore e consideriamo la sua velocità la massima
possibile e cioè c, allora Δt sarà anche dato da:
Pertanto lo spazio percorribile dal mediatore è dato da:
Nel caso di una diffusione tra elettroni, il quanto mediatore è il fotone che ha massa
nulla e quindi l’energia minima che esso può trasportare è zero: pertanto la portata
dell’interazione (“range”) è infinito.
Se invece il “quanto” che fa da mediatore dell’interazione ha massa m, la
minima energia da esso trasportata sarà pari a:
e quindi il range massimo dell’interazione non potrà essere infinito e sarà dato da:
Nel 1935 Yukawa, per spiegare il fatto che le interazioni forti tra adroni
mostravano di avere una portata (“range”) dell’ordine di 2 fm, propose l’idea che
il mediatore dell’interazione fosse una particella dotata di massa, il pione. Con
questa ipotesi, il “range” massimo dell’interazione si ha in corrispondenza
dell’energia minima da esso trasportata:
Potere risolutivo di una particella
Per “vedere” un oggetto occorre illuminarlo con una lunghezza d’onda che sia
comparabile o inferiore alle dimensioni dell’oggetto e che, interagendo con
esso, ne venga diffusa tutto intorno, colpendo l’occhio.
Se l’oggetto è più piccolo della lunghezza d’onda della luce usata per illuminarlo,
esso sarà “avvolto” dalla luce, che non potrà così interagire con esso. L’oggetto
non può essere osservato.
Potere risolutivo di una particella
Per “vedere” un oggetto occorre illuminarlo con una lunghezza d’onda che sia
comparabile o inferiore alle dimensioni dell’oggetto e che, interagendo con
esso, ne venga diffusa tutto intorno, colpendo l’occhio.
Se l’oggetto è più piccolo della lunghezza d’onda della luce usata per illuminarlo,
esso sarà “avvolto” dalla luce, che non potrà così interagire con esso. L’oggetto
non può essere osservato.
Con la luce visibile (e con l’uso di un microscopio ottico) possiamo risolvere
oggetti con dimensioni maggiori o uguali del nanometro, come le micromolecole.
Per risolvere l’atomo che ha dimensione ratomo ~ 10-10 m, occorre adoperare i
raggi X che hanno lunghezze d’onda dell’ordine di:
λ ~ 10-7 m – 10-11 m
Con i raggi γ che hanno lunghezze d’onda inferiori a 10-11 m si possono sondare
oggetti di dimensioni più piccole come nuclei o nucleoni.
Dato che una particella dotata di un certo impulso, possiede una lunghezza d’onda
fornita dalla relazione di de Broglie:
allora per “illuminare” oggetti molto piccoli, come i nuclei o i nucleoni, si
possono adoperare anche particelle materiali di impulso opportuno, che
vengono diffuse dalle particelle bersaglio.
La distanza minima che possiamo sondare con una particella di impulso p è fornita
dal principio di indeterminazione di Heisenberg:
La lunghezza d’onda
ci dà quindi una stima della taglia minima che si può
sondare con una particella di un certo impulso o, all’inverso, ci dice quale
impulso deve avere una particella per sondare oggetti di una determinata
dimensione.
Ad esempio, possiamo calcolare quale impulso minimo deve avere una particella
per poter risolvere il nucleo o un nucleone (il protone o il neutrone) o un quark:
I calcoli mostrati sono solo approssimativi. Andando avanti nello studio della
teoria della diffusione tra due particelle, scoprirete che in realtà il parametro
fondamentale per determinare la dimensione minima dell’oggetto esplorabile è
il quadrato del quadrimpulso trasferito dalla particella proiettile a quella
bersaglio, più che l’impulso del proiettile. Tuttavia il calcolo ci fornisce già un
ordine di grandezza delle energie minime che deve avere un fascio per sondare
un determinato bersaglio.
Nell’esperimento di Rutherford (1911), furono adoperate particelle α di energia
cinetica T ~ 2 MeV su nuclei di Au, che corrispondono a un impulso p:
Pertanto la lunghezza d’onda esplorata corrispondeva a:
→ Esattamente la dimensione di un nucleo!!
Pertanto, la diffusione di particelle su un bersaglio rappresenta un fondamentale
strumento per studiare le interazioni tra le particelle e per conoscere la struttura
interna delle particelle bersaglio, nel caso in cui il proiettile non sia dotato a sua
volta di struttura.
Scegliendo sonde di natura diversa (fotoni, leptoni, adroni) per sondare un
bersaglio, si decide di sondarlo attraverso tipi di interazioni differenti.
Ad esempio, se adoperiamo una:
1) sonda leptonica carica (e±, µ±) per studiare un bersaglio adronico (es. elettrone
su nucleo o elettrone su protone), la diffusione sarà dovuta principalmente alle
interazioni elettromagnetiche e non a quelle forti (perchè i leptoni sono particelle
non composte da quark); vi sono presenti anche quelle deboli, ma sono mascherate
dalle ben più intense interazioni e.m.;
2) sonda leptonica neutra (νe, νµ, νe, νµ) su un bersaglio adronico, la diffusione
sarà invece dovuta unicamente alle interazioni deboli e non a quelle forti (di nuovo
perchè i leptoni sono particelle non composte da quark) e neanche a quelle e.m.
(perchè i neutrini non hanno carica elettrica); pertanto i neutrini sono le sonde
privilegiate per studiare gli effetti delle interazioni deboli;
3) sonda adronica (pioni π± , kaoni K, protoni, antiprotoni) su un bersaglio
adronico, la diffusione sarà dovuta principalmente alle interazioni forti.












