Proprietà ondulatorie della materia: dualismo onda-particella
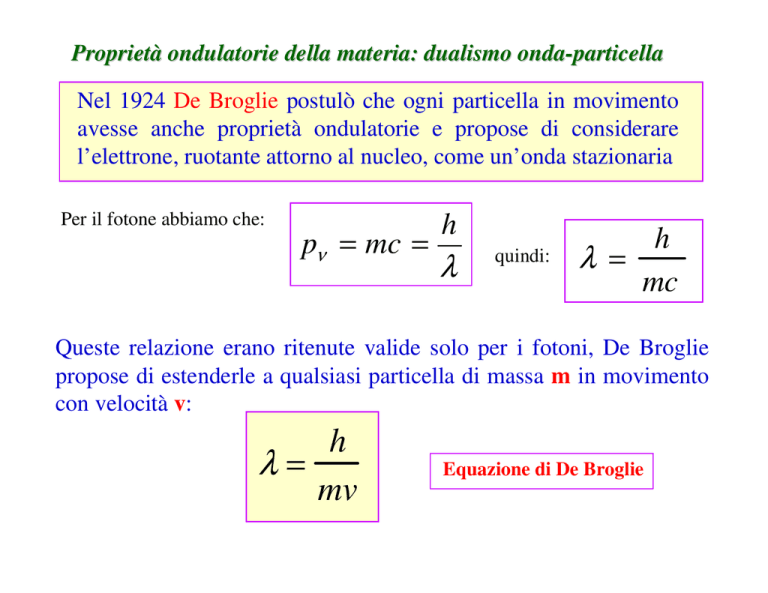
Nel 1924 De Broglie postulò che ogni particella in movimento
avesse anche proprietà ondulatorie e propose di considerare
l’elettrone, ruotante attorno al nucleo, come un’onda stazionaria
Per il fotone abbiamo che:
pν = mc =
h
λ
quindi:
h
λ =
mc
Queste relazione erano ritenute valide solo per i fotoni, De Broglie
propose di estenderle a qualsiasi particella di massa m in movimento
con velocità v:
h
λ=
mv
Equazione di De Broglie
Ipotesi di De Broglie
Circonferenza
2° postulato di Bohr
2π r = n λ
Applichiamo la relazione di De Broglie al moto dell’elettrone attorno al
nucleo; affinchè l’elettrone possa rimanere in uno stato stazionario deve
descrivere un’onda stazionaria e quindi la circonferenza dell’orbita deve
essere un numero intero di lunghezze d’onda:
n λ = 2π r
quindi dato che:
h
λ=
mv
possiamo scrivere:
h
2π r
=
mv
n
rielaborando questa uguaglianza otteniamo:
h
mvr = n
2π
1° Postulato di Bohr
Diffrazione di un fascio di
raggi luminosi attraverso
un piccolo foro (a,b).
Diffrazione di
un fascio di
raggi X (c,d) e di
un fascio di
elettroni (c,e) al
passaggio
attraverso una
sottile foglia di
argento
policristallino
Dualismo onda particella
Radiazione
elettromagnetica (luce)
Fascio di fotoni
Foglio metallico policristallino
o cristallo
Fascio di elettroni
Elettroni
1927, Davisson, Germer e Thomson
Principio di indeterminazione di Heisenberg (Nobel 1932)
È impossibile determinare con precisione contemporaneamente la
posizione e la velocità di una particella di massa molto piccola
fotone
microscopio
microscopio
fotone
elettrone
elettrone
Principio di indeterminazione di
Heisenberg
∆x · ∆(m · vx) ≅ h
∆y · ∆(m · vy) ≅ h
∆z · ∆(m · vz) ≅ h
h: costante di Planck
h = 6,62 10-34 J . s
(6,62 10-27 erg . s)
Principio di indeterminazione di Heisenberg
Sfera di massa m = 10-5 g
∆ ⋅∆
≅
∆ =
−
=
⋅
−
⋅
−
∆
=
=
−
⋅
−
⋅
⋅
−
−
⋅
Incertezza trascurabile
Elettrone m = 10-27 g
∆ ⋅∆
≅
∆ =
−
=
⋅
−
⋅
−
∆
=
⋅
=
⋅
⋅
−
−
vx indeterminata












