Trigonometria
1°Teorema
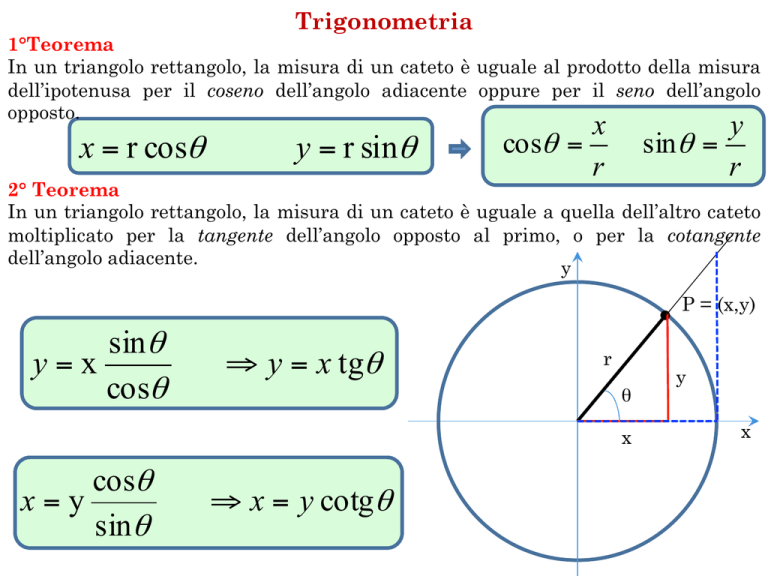
In un triangolo rettangolo, la misura di un cateto è uguale al prodotto della misura
dell’ipotenusa per il coseno dell’angolo adiacente oppure per il seno dell’angolo
opposto.
x = r cosθ
y = r sinθ
x
cosθ =
r
y
sinθ =
r
2° Teorema
In un triangolo rettangolo, la misura di un cateto è uguale a quella dell’altro cateto
moltiplicato per la tangente dell’angolo opposto al primo, o per la cotangente
dell’angolo adiacente.
y
P = (x,y)
sinθ
y=x
cosθ
⇒ y = x tgθ
r
y
θ
x
cosθ
x=y
sinθ
⇒ x = y cotgθ
x
Funzioni trigonometriche
Le funzioni trigonometriche (sin, cos, tan, cotan, …) sono funzioni periodiche, cioè
che dopo un determinato periodo si ripetono identiche a loro stesse; per le funzioni
seno e coseno il periodio è pari a 2π (360°), per la tangente e la cotangente il periodo
è pari a π
y
y = tan x
y = cosx
y = sinx
y
x
-π/2
π/2
0
-1 ≤ cosx ≤ 1
1
x
cosx
tanx
-1≤ sinx ≤1
cotanx
sinx
Periodo
Periodo
-∞<tanx<∞
π
x
Identità trigonometriche
a = c cosθ
c
b = c sinθ
b
θ
a
sin 2 θ + cos 2 θ = 1
sin(θ ± φ ) = sin θ cos φ ± cosθ sin φ
sin 2θ = 2 sin θ cosθ
cos(θ ± φ ) = cosθ cos φ ∓ sin θ sin φ
cos 2θ = cos 2 θ − sin 2 θ
⎡1
⎤
⎡1
⎤
sin θ ± sin φ = 2 sin ⎢ (θ ± φ )⎥ cos⎢ (θ ∓ φ )⎥
⎣2
⎦
⎣2
⎦
sin 2
θ
cos 2
θ
2
2
=
1
(1 − cosθ ) ⇒ (1 − cosθ ) = 2 sin 2 θ
2
2
=
1
(1 + cosθ )
2
tan 2θ =
tan
θ
2
=
2 tan θ
1 − tan 2 θ
1 − cosθ
1 + cosθ
⎡1
⎤
⎡1
⎤
cosθ + cos φ = 2 cos⎢ (θ + φ )⎥ cos⎢ (θ − φ )⎥
⎣2
⎦
⎣2
⎦
⎡1
⎤ ⎡1
⎤
cosθ − cos φ = 2 sin ⎢ (θ + φ )⎥ sin ⎢ (θ − φ )⎥
⎣2
⎦ ⎣2
⎦
tan 2θ =
2 tan θ
1 − tan 2 θ
Formule di Prostaferesi
Grandezze Scalari e Grandezze Vettoriali
Massa, temperatura, distanza,
intervallo temporale, energia,
lavoro, potenza …
Spostamento, velocità,
accelerazione, forza, momento
angolare, momento di una forza …
Grandezza completamente
definita da un VALORE
NUMERICO (positivo o
negativo) espresso nell’unità di
misura appropriata
Grandezza completamente definita
da un valore numerico positivo,detto
MODULO, espresso nell’unità
appropriata, da una DIREZIONE e
da un VERSO
Scalari
Vettori
Aritmetica ordinaria
somma, sottrazione,
moltiplicazione, divisione,…
Algebra vettoriale
somma e sottrazione di vettori,
proiezioni, prodotto scalare, prodotto
vettoriale, …
Vettori
Ø Un vettore si rappresenta graficamente attraverso una freccia
Ø Si indica:
§ Con una lettera in grassetto :
§ Con una lettera e una freccia :
§ Con gli estremi e una freccia :
a
!
a
B
!
a
AB
a
La lunghezza del corpo della
freccia indica il modulo
La retta su cui giace la freccia
indica la direzione
A
La punta della freccia
indica il verso
Caso particolare di vettore:
Versore: vettore adimensionale di lunghezza unitaria
introdotto per specificare una data direzione orientata:
Es:
Sono i VERSORI della TERNA CARTESIANA x,y,z
iˆ, ˆj , kˆ
Notazione: ⊗ Vettore entrante nel foglio
â
a=1
Vettore uscente
Somma di Vettori(1)
• Non possono essere sommati vettori associati a grandezze diverse
• Non possono essere sommati vettori associati alla stessa grandezza ma espressi con
unità di misura diverse ( bisogna prima effettuare una conversione ad un’unità di
misura comune)
!
!
A(cm ) + B (mm)
!
A(cm )
!
B (mm )
Conversione di unità di misura
!
(moltiplicando il modulo di B per
!
!
A(cm) + B(cm)
1cm
)
10mm
!
A(cm )
!
B (cm )
Somma di Vettori (metodo geometrico)(2)
!
B
!
A
! !
A+ B =
!
B
!
A
Regola del
parallelogramma
! ! !
R = A+ B
!
C
! !
A+ B
! ! ! !
R = A+ B +C
! ! ! !
R = A+ B +C
(
Proprietà
Commutativa della
somma
!
A
! ! ! ! !
R = A+ B = B + A
!
B
!
B
!
A
! ! !
R = B+ A
)
!
B
!
B
! !
B+C
!
A
! ! ! !
R = A+ B +C
(
! ! !
R = A+ B
!
A
)
!
C
Proprietà
associativa della
somma
! ! ! ! ! ! !
R = A+ B +C = A+ B +C
! ! ! ! ! !
= A+ B +C = B + A+C
(
(
)
)
(
)
Vettore opposto
e Differenza di!Vettori
!
Si definisce opposto del vettore A quel vettore che sommato ad A dà come risultato 0
!
Ma quale è quel vettore che sommato ad A mi dà zero?
!
A
!
A
! ! !
R = A+ B
! ! !
R = A+ B
!
B
!
B
!
A
! ! !
R = A+ B = 0
!
B
!
A
!
−A
!
!
A+ − A = 0
( )
!
!
I vettori A e − A hanno stesso modulo e direzione, ma verso opposto
Possiamo vedere la sottrazione come la somma di un vettore con l’opposto dell’altro
!
B
!
A
!
B
!
−B
! ! !
!
A− B = A+ − B
( )
! ! !
R = A− B
!
−B
!
A
!
B
! ! !
R = A− B
Moltiplicazione di un vettore per uno scalare
!
!
Il prodotto s A di un vettore A per un numero s (scalare) è un vettore avente:
!
Ø direzione uguale a quella! di A ;
Ø verso uguale a quello di A! se s>0;
Ø verso opposto a quello di A se s<0;
Ø se s=0 si ottiene il vettore nullo;
Ø modulo uguale
al prodotto tra il
!
modulo di A e il valore assoluto di s.
s= 2
!
A
!
A
!
sA =
s= -2
!
2A
!
2A
!
− 2A
Vettori (nello spazio tridimensionale)
q Un vettore è rappresentato graficamente da un segmento, la cui lunghezza o “modulo”, una
volta fissata l’unità di misura, definisce l’intensità del vettore stesso
!
A1
!
A
z
!
A2
!
B
P
θ
!
A3
O
y
φ
! ! !
A1 , A2 , A3
!
A=
! ! !
!
A = A1 = A2 = A3
x
Vettore libero
Vettori equipollenti:
Due vettori si dicono uguali se
hanno stesso modulo e puntano
nella stessa direzione e verso
!
B
Vettore definito univocamente
!
dal punto di applicazione (B,P)
!
B
Ø Il modulo del vettore è pari alla lunghezza del segmento OP
!
Ø La direzione del vettore B nello spazio è definita dai due angoli θ e φ che il vettore forma con
all’asse z e con il piano xy (della terna cartesiana scelta) rispettivamente
Componenti di Vettori e Versori(1)
q Il metodo geometrico per la somma di vettori diventa complicato da attuare quando si ha bisogno di
descrivere i vettori nello spazio tridimensionale
q Conviene utilizzare un metodo più analitico che fa uso delle proiezioni di un vettore lungo gli assi
di un sistema cartesiano ( sistema di coordinate ortogonali … sperando che questa sia una
puntualizzazione ovvia)
q Se con la somma troviamo un vettore che rappresenta la combinazione di uno o più vettori,
analogamente si può anche scomporre un vettore nella somma di altri due o più vettori
( Decomposizione)
!
I Valori numerici Ax, Ay, Az sono le proiezioni di A sui
rispettivi assi x, y, z
Az
iˆ, ˆj , kˆ sono i versori,della terna cartesiana.
In particolare:
• iˆ è diretto lungo l’asse positivo delle x
• ĵ è diretto lungo l’asse positivo delle y
• k̂ è diretto lungo l’asse positivo delle z
z
!
A
P
θ
Ax
x
iˆ
k̂
O
ĵ
Ay
y
φ
Axiˆ, Ay ˆj, !Az kˆ
vettore A
!
A
Possiamo quindi riscrivere il vettore
intermini dei tre
versori iˆ, ˆj , kˆ e delle sue proizioni
!
A = Axiˆ + Ay ˆj + Az kˆ
sono a loro volta 3 vettori la cui somma dà il
Vettori e componenti
Un vettore, una volta scelti gli assi cartesiani, può essere individuato anche tramite le sue
componenti lungo tali assi:
!
! !
A = Axiˆ + Ay ĵ = Ax + Ay
y
Ay
!
A
!
Ay = Ay ˆj
ĵ
O iˆ
I vettori componenti: hanno per modulo il valore
assoluto delle componenti e direzione del versore
associato all’asse di proiezione Il verso può essere
lo stesso od opposto del versore associato.
P
Teorema di Pitagora
A
θ
!
Ax = Axiˆ
Ay
q Modulo:
θ
Ax x
Ax = A cosθ ⎫⎪
Ay sin θ
⇒
=
= tan θ
⎬
A
cos
θ
x
Ay = A sin θ ⎪⎭
!
A = A = Ax2 + Ay2
Ax
q Angolo θ : tan θ
NB: le proiezioni di un vettore possono essere anche negative
=
Ay
Ax
Somma per componenti
Abbiamo visto che un vettore può essere espresso mediante le sue componenti lungo gli assi cartesiani
Domanda:
!
!
Come si fa a sommare ad un vettore A di componenti Ax e Ay un vettore B di componenti Bx e By?
Risposta:
Si sommano le componenti lungo x e lungo y separatamente
!
! ! !
B , sia R = A + B il vettore risultante dalla somma di essi.
!
A = Ax iˆ + Ay ˆj ⎫ ! ! !
⎪ R = A + B = Ax î + Ay ĵ + Bx î + By ĵ = Ax + Bx î + Ay + By ĵ
!
⎪
B = Bx iˆ + B y ˆj ⎬
Rx
Ry
⎪
!
R = Rx iˆ + Ry ˆj⎪
y
⎭
!
Dati i due vettori A e
(
) (
) (
) (
Modulo
2
2
R = Rx + R y =
Angolo
(Ax + Bx ) + (Ay + By )
2
Ry Ay + By
tan θ =
=
Rx Ax + Bx
2
Ry
!
R
By
Ay
O
Rx = Ax + Bx
)
R y = Ay + B y
!
B
θ !
A
Ax
Bx
Rx
x
Moltiplicazione di vettori
I vettori sono quantità più complicate degli scalari
‼ la somma di due scalari è una semplice operazione algebrica
( es: 2 s +3 s = 5 s senza ambiguità)
‼ la somma di due vettori non è la semplice somma delle intensità dei due
vettori, ma un’operazione che tiene conto anche della direzione e del verso
che i due vettori hanno l’uno rispetto all’altro
Lo stesso discorso vale per la moltiplicazione tra vettori… tanto che, se per
gli scalari esiste un’unica operazione di moltiplicazione, per i vettori ne
esistono 2.
1) Prodotto scalare
! !
A ⋅ B = Scalare
“A scalar B”
2) Prodotto vettoriale
! !
A × B = Vettore
“A vector B”
Moltiplicazione di vettori-Prodotto scalare(1)
! !
!
!
Il prodotto scalare di due vettori A e B, si scrive A ⋅ B è una grandezza
scalare uguale al prodotto dei moduli dei due vettori con
dell’angolo (θ) formato tra di essi (l’angolo minore dei due)
il coseno
y
!
A≡A
R
θ
!
B
2π-θ
θ
2π-θ
!
A
x
Rcosθ
R
! !
A ⋅ B ≡ A B cos(2π − θ ) = A B cosθ
cos(2π − θ ) = cos
π cosθ + sin
π sin θ = cosθ + 0 = cosθ
#"2!
#"2!
1
!
!
Prodotto scalare tra A e B
! !
A ⋅ B ≡ AB cosθ
0
cos(2π − θ ) = cosθ
Altro modo di vedere il prodotto scalare:
! !
A e B è una grandezza scalare
Il prodotto scalare di due vettori qualsiasi
!
!
!
uguale al prodotto del modulo di A moltiplicato per la proiezione di B su A
!
B
!
B
!
A
Proiezione di
B
θ
B cosθ
!
A
!
!
su
B A
! !
A ⋅ B ≡ AB cosθ
Moltiplicazione di vettori-Prodotto scalare(2)
Proprietà del prodotto scalare e casi particolari:
Ø Il prodotto scalare PUÒ avvenire tra vettori con unità di misura diverse e le unità di misura del
risultato del prodotto sono semplicemente il prodotto delle unità di misura (ne vedremo diversi esempi)
Ø Proprietà Commutativa
Ø Proprietà distributiva della moltiplicazione:
! !
Ø Se A // B il loro prodotto scalare è pari ad AB:
! ! ! !
A⋅ B = B ⋅ A
! ! !
! ! ! !
A⋅ B + C = A⋅ B + A⋅C
! !
A ⋅ B = AB cos
0° = A B
!
(
)
=1
! !
Ø Se A ⊥ B il loro prodotto scalare è nullo:
! !
Ø Se A = B = 0 il loro prodotto scalare è nullo:
Ø Se consideriamo i tre versori ortogonali iˆ, ˆj , kˆ
iˆ ⋅ iˆ = ˆj ⋅ ˆj = kˆ ⋅ kˆ = 1
iˆ ⋅ ˆj = iˆ ⋅ kˆ = ˆj ⋅ kˆ = 0
! !
A ⋅ B = AB cos
90° = 0
"#$
=0
! ! ! !
A⋅ B = 0 ⋅ 0 = 0
Moltiplicazione di vettori-Prodotto scalare(3)
Definito un sistema di coordinate cartesiane di riferimento, il prodotto scalare si può anche
scrivere nella forma:
! !
A ⋅ B ≡ Ax Bx + Ay By + Az Bz
(dimostrazione alla lavagna)
Ed in particolare:
! !
A ⋅ A ≡ Ax Ax + Ay Ay + Az Az = Ax2 + Ay2 + Az2 = A2
Le due equazioni che descrivono il prodotto scalare:
! !
A ⋅ B ≡ AB cosθ
! !
A ⋅ B ≡ Ax Bx + Ay By + Az Bz
sono del tutto equivalenti
La scelta di una o dell’altra per determinare il prodotto scalare dipende da
come vengono definiti i vettori
Moltiplicazione di vettori-Prodotto vettoriale(2)
! !
!
!
Il prodotto vettoriale di due vettori A e B, si scrive A × B ed è un vettore
che:
Ø ha modulo pari al prodotto dei moduli dei due vettori moltiplicati per il
seno dell’angolo (α) minore compreso tra essi.
! ! !
C = A× B
!
B
α
2π − α
Modulo
!
A
!
C ≡ C = AB sin α
y
NB: sin α ≠ sin(2π − α )
R
sin (2π − α ) = sin
π cos α − sin α cos
π = − sin α
#"2!
#"2!
0
θ
1
2π-θ
R
Rsinθ
x
Rsin(2π-θ)
!
Ø La direzione di C è PERPENDICOLARE al piano definito dai due vettori
Ø Il verso è quello dato dalla regola della mano destra.
Moltiplicazione di vettori-Prodotto vettoriale(2)
! !
a × b = ab
! !
a×b = 0
! !
a×a =0
Se i due vettori sono ORTOGONALI (θ=90° => sin θ=1)
Se i due vettori sono PARALLELI
! !
! !
a×b =− b×a
! ! !
! ! !
a⋅ a×b = b⋅ a×b = 0
(
)
(
(
)
)
(
)
(θ=0° => sin θ=0)
Calcolo differenziale
dove a,b,c,d sono valori costanti fissati.
y può essere definita per ogni valore di x.
Es: x=1 => y(1)=a+b+c+d ;
x=2 => y(2)=8a+4b+2c+d; …
La derivata di y(x) rispetto ad x è definita come il
limite al tendere di Δx a 0 delle corde tracciate fra
due punti sulla curva y:
y+Δy
Definiamo una funzione f(x) che mette in relazione le variabili indipendente x con la
variabile (dipendente) y:
Corda
y(x)
y(x)
f ( x) = y( x) = ax 3 + bx 2 + cx + d
Δy
y
Δx
x
( x + Δx) − x
NB:La derivata di y(x) risulta essere la pendenza
della tangente alla curva y(x) nel punto x
(lo vedremo meglio tra poco applicato alla velocità)
x
Tangente alla
curva nel punto
(x,y(x))
y(x)
y ( x + Δx) − y ( x)
dy
Δy
y' =
= lim
= lim
dx Δx→0 Δx Δx →0
Δx
Derivata di y(x) rispetto ad x
x+Δx
y
x
x
Derivate definite
da
=0
dx
a = cost
d ax n
= nax n −1
dx
a = cost
d sin x
= cos x
dx
d sin ax
= a cos ax
dx
a = cost
d cos x
= − sin x
dx
d cos ax
= −a sin ax
dx
a = cost
d tan x
1
=
dx
cos2 x
d tan ax
a
=
dx
cos2 ax
de ax
= ae ax
dx
d ln ax 1
=
dx
x
La derivata di una costante è identicamente nulla
dx n
= nx n −1
dx
dx 4
= 4x 3
dx
( )
Proprietà delle derivate
Derivata di una somma(differenza) di funzioni:
d
[ f (x ) ± g (x )] = df ± dg
dx
dx dx
Prodotto di funzioni:
d
[ f (x )g (x )] = f dg + g df
dx
dx
dx
Rapporto di funzioni:
d
[ f (x ) g (x )] =
dx
g
df
dg
−f
dx
dx
g2
Funzione di funzione:
d
df dg
g ( f (x )) =
dx
dx df
d
(4 x 2 + 3 sin 2 x) = 8 x + 6 cos 2 x
dx
d 3
[ x cos 3 x] = − x 3 ⋅ 3 sin 3x + cos 3x ⋅ 3x 2 =
dx
3 x 2 cos 3x − 3x 3 sin x
d ⎡ cos 3x ⎤ − x 3 ⋅ 3 sin 3x − cos 3x ⋅ 3x 2
=
=
3
6
⎢
⎥
dx ⎣ x ⎦
x
x sin 3x + cos 3x
− 3x 2
=
6
x
x sin 3x + cos 3x
−3
x4
y ( x) = cos x,
g ( y) = y 2
d
(cos x) 2 = 2#cos
x⋅−
sin
x = −2 sin x cos x
"
!
#
"
!
dx
d
dy ( x )
dx
g(y)
dx
Calcolo integrale
L’integrazione è da considerare la funzione inversa della derivata
L’integrale I della funzione f(x) tra i limiti a e b si scrive:
x =b
∫ f ( x)dx = I ( x)
b
a
= I (b) − I (a)
f(x)
f(x)
x=a
ed è pari all’area compresa tra la curva f(x) e l’asse delle x
nell’intervallo di valori a≤ x≤b
NB:
Se il limite superiore dell’integrale è una variabile w si ha :
x=w
I ( w) =
∫
f ( x)dx
x=a
allora
a
b
x
x=w
d
d
I ( w) =
f ( x)dx = f ( w)
dw
dw x∫= a
e quindi in generale:
L’integrale indefinito I(x) di f(x) è la funzione la cui derivata è f(x)
Es:
a
b
∫ (ax
1
)
+ bx + c dx = x 3 + x 2 + cx + d
3
2
1
b
b
b
⎛a
⎞ ⎛a
⎞ ⎛a
⎞ a b
ax 2 + bx + c dx = ⎜ x3 + x 2 + cx + d ⎟ = ⎜ 13 + 12 + c1 + d ⎟ − ⎜ 03 + 02 + c0 + d ⎟ = + + c
2
2
2
⎝3
⎠0 ⎝3
⎠ ⎝3
⎠ 3 2
∫(
0
2
)
Calcolo Integrale(2)
L’integrale I ( x) = f ( x)dx è detto primitiva di f(x), cioè è quella funzione che
quando derivata dà la funzione f(x)
∫
NB: l’integrale è definito sempre a meno di una costante, cioè esistono infinite
primitive di una stessa funzione, tutte quelle che differiscono tra di loro per una
costante, in quanto la derivata di una costante è comunque nulla.
Proprietà degli integrali:
∫ dx = x + c
df (x )
∫ dx dx = f ( x) + c
∫ af (x)dx = a∫ f ( x)dx
dove a = cost
∫ [af ( x) + bg ( x)]dx = a∫ f ( x)dx + b∫ g ( x)dx
'
'
∫ f ( x) g ( x)dx = f ( x) g ( x) − ∫ g ( x) f ( x)dx
L’integrale di una funzione moltiplicata per una
costante è uguale alla costante per l’integrale della
funzione
L’integrale di una somma di funzioni è uguale alla
somma degli integrali delle singole funzioni
Integrazione per parti: date due funzioni di x f e g
l’integrale della derivata di f moltiplicata per g è uguale
al prodotto delle due funzioni meno l’integrale della
derivata di g moltiplicata per f.










