3a Esercitazione: soluzione
Monica Bonacina ([email protected])
Corso di Microeconomia A-K, a.a. 2010-2011
De…nizioni. Si de…niscano sinteticamente i termini anche con l’ausilio, qualora
necessario, di formule e gra…ci.
Def. 1. Equivalente certo di una lotteria.
Soluzioni. In presenza di una lotteria cui è associata un’utilità attesa, l’equivalente
certo è quel valore che, se garantito con certezza, rende l’agente indi¤ erente tra il
partecipare o meno alla lotteria.
Def. 2. Informazione nascosta.
Soluzioni. Situazione nella quale una parte del mercato non è in condizione di
valutare in maniera completa la qualità dei beni/servizi o¤ erti.
Def. 3. Amante del rischio (o propenso al rischio).
Soluzioni. Un individuo che preferisce una prospettiva incerta con un determinato valore atteso, piuttosto che una certa con lo stesso valore atteso. Oppure Si
dice avverso al rischio un soggetto che fra due lotterie con il medesimo valore atteso
preferisce quella con minor varianza.
Def. 4. Azione nascosta.
Soluzioni. Azione di chi, potendo contare su una fonte più ampia di informazioni, ha lìopportunità di modi…care l’esito di un contratto (a proprio vantaggio)
a danno della sua controparte.
Def. 5. Lotteria.
Soluzioni. Una lotteria è una variabile casuale i cui valori sono somme monetarie.
Def. 6. Utilità attesa di una lotteria.
Soluzioni. L’utilità attesa è il valore atteso dell’utilità di ciascuno dei possibili
risultati di una lotteria.
1
Def. 7. Indi¤erente al rischio.
Soluzioni. Un individuo per il quale tutte le possibilità con lo stesso valore atteso
si equivalgono, indipendentemente dal rischio che comportano.
Vero/Falso. Si stabilisca se gli enunciati sono veri, falsi, o incerti. Si fornisca una spiegazione (anche gra…ca se opportuno) e si argomenti compiutamente la
risposta.
Vero/Falso 1. Se la funzione di utilità di un individuo è concava, allora questi
sarà sicuramente avverso al rischio.
Soluzioni. VERO. Per un individuo avverso al rischio, l’utilità cresce sempre
meno all’aumentare della vincita. La funzione di utilità corrispondente è quindi concava.
Vero/Falso 2. Si consideri una lotteria cui è associato un certo valore atteso, EV.
L’equivalente certo di questa lotteria per un individuo avverso al rischio è sicuramente
maggiore dell’equivalente certo di un individuo propenso al rischio.
Soluzioni. FALSO. L’equivalente certo di un individuo avverso al rischio è
minore del valore atteso della lotteria, mentre l’equivalente certo di un individuo
amante del rischio è superiore al valore atteso della lotteria. Quindi, data la lotteria,
l’equivalente certo dell’individuo propenso al rischio è maggiore dell’equivalente certo
dell’individuo avverso al rischio.
Vero/Falso 3. In presenza di informazione nascosta, uno scambio avvantaggia
sempre la parte meglio informata.
Soluzioni. FALSO. Consideriamo il caso di vantaggio informativo dei produttori sui consumatori e supponiamo che malgrado l’asimmetria informativa avvengano
scambi di prodotti sia di alta che di bassa qualità. I produttori di beni di bassa qualità
si avvantaggiano dello scambio a discapito vuoi di quella parte di consumatori (imperfettamente informati) che scoprono di aver acquistato beni di bassa qualità, vuoi
dei produttori di beni di alta qualità (perfettamente informati) che sono costretti ad
accettare un prezzo inferiore alla reale disponibilità a pagare dei consumatori per il
loro prodotto.
Vero/Falso 4. La presenza di franchigie nei contratti di assicurazione è intesa a
correggere problemi di informazione nascosta.
Soluzioni. FALSO. Lasciando a carico dell’assicurato la copertura di parte del
danno subito, le franchigie nei contratti di assicurazione cercano di correggere problemi di azione nascosta (comportamento negligente o azzardo morale).
Vero/Falso 5. Un soggetto propenso al rischio preferisce partecipare ad una lotteria piuttosto che ricevere una somma certa.
Soluzioni. INCERTO. Dipende dall’ammontare della soma certa che viene
o¤ erta. Un individuo propenso al rischio preferisce partecipare ad una lotteria piuttosto che ricevere con certezza una somma pari al valore atteso della lotteria.
Vero/Falso 6. Si consideri un mercato caratterizzato dalla seguente curva di domanda: Q = 10 p. In seguito ad un aumento dell’1% del prezzo, la quantità
2
domandata diminuirà dell’1%.
Soluzioni. In generale FALSO. Dalla forma della curva di domanda si ricava
la seguente elasticità della domanda al prezzo " = (@Q=@p)p=Q = p=Q che non
risulta essere costantemente uguale a -1; infatti " = 1 se e solo se -p/Q=-1 ovvero
se p=Q.
Vero/Falso 7. Si consideri il modello di scelta intertemporale. Consumo oggi (C1 )
e consumo domani (C2 ) sono per Susanna perfetti complementi. Se il tasso (r) al
quale Susanna può dare o prendere a prestito diminuisce, allora la consumatrice
deciderà di diminuire il consumo in entrambi i periodi.
Soluzioni. INCERTO. L’e¤ etto della contrazione di r sulle decisioni di consumo di Susanna dipende da dove si trova il paniere delle dotazioni iniziali rispetto
alla retta dei vertici e quindi dal livello di investimento o di indebitamento iniziale
della consumatrice.
Esercizi. Si risolvano i seguenti esercizi.
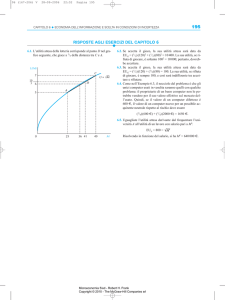
Esercizio 1. Supponete che la domanda di attraversamenti del tunnel sotto la
Manica sia Q = 1000 100P . (1) Se il pedaggio è P = 6 euro, qual è la spesa
totale in attraversamenti? Se ne fornisca una rappresentazione gra…ca. (2) Si calcoli
l’elasticità della domanda al prezzo in corrispondenza dell’equilibrio individuato al
punto 1. (3) E’possibile ridurre la spesa totale per attraversamenti aumentando il
prezzo del pedaggio? Perchè? Si risponda con l’ausilio di un gra…co.
La compagnia di traghetti R&W lines sta valutando se investire in una nuova
‡otta di traghetti. L’introduzione di questi nuovi traghetti porterebbe ad una notevole riduzione del costo (e quindi del prezzo) dell’attraversamento via mare. (4) Supponendo che la compagnia R&W lines e l’impresa gestrice del tunnel sotto la manica
operino in regime di concorrenza, che e¤etto potrebbe avere la strategia di R&D sulla
domanda di attraversamenti del tunnel sotto la manica? Argomentate la risposta.
Soluzioni. (1) Stante il pedaggio per gli attraversamenti ( P = 6), la domanda
di attraversamenti sarà pari a
Q = 1000
100P = 400
da cui una spesa totale (ST)
ST = Q P = 2400
(2) L’elasticità della domanda di attraversamenti al prezzo in corrispondenza dell’equilibrio
individuato al punto (1) è
"=
@Q P
@p Q
=
6
100 400
=
3
2
=
1; 5
(3) Dal momento che la domanda è elastica, un aumento nel prezzo degli attraversamenti dell’1% comporterà una diminuzione più che proporzionale nella domanda di
attraversamenti; è quindi possibile ridurre la spesa totale in attraversamenti aumentando il prezzo. La spesa totale è
Q
100
ST = P Q = Q 10
= 10Q
Q2
100
ed è massima quando
@ST
@Q
= 0 ! 10
Q
50
= 0 ! Q = 500; P = 5
3
P
10
Curva di domanda inversa
Tratto elastico della curva di domanda
Equilibrio iniziale
6
5
Tratto anelastico della
curva di domanda
Elasticità unitaria
400
500
1000
Q
Andamento della spesa totale
ST
2500
2400
400
500
1000
Q
(4) Una riduzione del prezzo …no a P=5 comporterà un aumento della domanda di
attraversamento più che proporzionale (siamo lungo il tratto elastico della domanda);
ulteriori contrazioni nel pedaggio aumenteranno la domanda in maniere meno che
proporzionale in quanto si veri…cheranno in corrispondenza del tratto anelastico della
curva.
Esercizio 2. Il signor Tettys Cicada non ha alcun reddito nel 2010 (M1 = 0), ma
sa già che nel 2011 guadagnerà un reddito pari a 110 (M2 = 110). Il pane del 2010
(C1 , in ascissa) e quello del 2011 (C2 ) hanno prezzo pari a 1; il tasso di interesse è del
10% (r = 10%); le preferenze di Tettys sono rappresentate dalla seguente funzione di
0:7
utilità: C0:7
1 C2 . (1) Rappresentate gra…camente il vincolo di bilancio intertemporale
di Tettys, indicando i valori di intercetta, l’inclinazione ed il paniere delle dotazioni.
(2) Individuate la scelta ottima di Tettys. Dite anche quanto risparmia, o di quanto
si indebita Tettys nel 2010. (3) Calcolate la domanda di pane nel 2010 in funzione
di M2 e r; calcolate l’elasticità della domanda di pane del 2010 al tasso di interesse e
al reddito M2 . (4) Discutete l’e¤etto di un aumento del 10% nel reddito nel secondo
periodo sul consumo nel primo periodo.
Soluzioni. (1) Il vincolo di bilancio intertemporale (in valore futuro) del consumatore è
(1 + r)C1 + C2 = (1 + r)M1 + M2
da cui
C2 =
1; 1C1 + 110
(2) Stante la forma delle preferenze di Tettys, da cui si ricava un saggio marginale
di sostituzione
0;7 C2
M UC1
C2
M RS = M
UC2 = 0;7 C1 = C1 ;
il paniere ottimo è ottenuto risolvendo il sistema
vincolo di bilancio
!
condiz di tangenza
C2 =
C2
C1
4
1; 1C1 + 110
!
=1+r
2; 2C1 = 110
C2 = 1; 1C1
C2
Paniere delle dotazioni
110
Vincolo di bilancio
-1,1
100
C1
da cui
C1 = 50
C2 = 55
ed il livello di indebitamento di Tettys è quindi pari a
S = M1
C1 =
C2
110
50
Paniere delle dotazioni
Vincolo di bilancio
55
E*
-1,1
50
100
C1
(3) La domanda di pane del 2010 si ottiene risolvendo un sistema analogo a quello
al punto (2), mantenendo incogniti il reddito nel secondo periodo ( M2 ) e il tasso di
interesse (r) da cui
vincolo di bilancio
!
condiz di tangenza
C2 =
(1 + r)C1 + M2
! C1 =
=1+r
C2
C1
M2
2(1+r)
I valori dell’elasticità della domanda di pane del 2010 al tasso di interesse ed al
reddito sono
r
1 =C1
"c1;r = Cr=r
= Cr1 Cr1 = 1+r
"c1;M2 =
C1 =C1
M2 =M2
=
C1 M2
M2 C1
=1
(4) Un aumento del 10% di M2 comporterà un aumento del 10% di C 1 :
5
Esercizio 3. La Medium Job fa settimanalmente colloqui di lavoro per assumere
i dipendenti del suo nuovo stabilimento. I candidati si presentano tutti vestiti allo
stesso modo e con lo stesso curriculum, ma metà di essi sono più e¢ cienti degli
altri. La Medium Job sa questa cosa ma non riesce in alcun modo a distinguere tra
le due tipologie di candidati. (1) Discutete il problema fronteggiato dalla Medium
Job e rappresentate questa situazione con le categorie economiche che conoscete. (2)
L’incapacità di distinguere tra le tipologie di candidati incida sui contratti o¤erti dalla
Medium Job? In che modo? Rispondete alla domanda speci…cando le di¤erenze tra
quanto vi aspettate che accada nella situazione qui descritta e quanto si veri…cherebbe
se la Medium Job riuscisse a distinguere i candidati. (3) Quale soluzione potrebbero
ideare la Medium Job e i candidati più e¢ cienti per tentare di risolvere il problema
discusso al punto precedente?
Soluzioni. (1) Questo è chiaramente un problema di informazione asimmetrica, in particolare di informazione nascosta. Una delle due parti dello scambio
(l’acquirente, Medium Job) è meno informata dell’altra (i candidati) circa la qualità dell’oggetto che si sta per scambiare (l’e¢ cienza delle prestazioni lavorative). La
prima parte (Medium Job) ottiene risultati diversi a seconda della qualità dell’oggetto
scambiato (lavoro), ma non è in grado di conoscere tale qualità, a di¤ erenza dell’altra
parte, verosimilmente a causa di un comportamento di coloro che sono caratterizzati da qualità bassa (bassa e¢ cienza). Da non confondere il caso di con “azione
nascosta” (asimmetria di informazione sul comportamento tenuto da una delle parti
durante l’esecuzione di un contratto).
(2) Se la Medium Job potesse distinguere i candidati, sarebbe disposta a pagare di
più i lavoratori più e¢ cienti: si formerebbero due mercati separati per le due qualità,
e sul mercato della qualità migliore sia la curva di domanda sia quella d’o¤ erta sarebbero spostate più in alto rispetto all’altro mercato, con un conseguente maggior prezzo
di equilibrio. Non potendo distinguere i candidati, per ogni diversa quantità di lavoro
la Medium Job sarà disposta ad o¤ rire una paga pari ad una media ponderata fra il
prezzo alto e quello basso che vorrebbe pagare in caso di informazione simmetrica: i
pesi della media sono inizialmente 1/ 2 e 1/ 2, poiché Medium Job sa che questa è la
proporzione dei due tipi. In altri, termini, la Medium Job si presenta sui due mercati
con la medesima curva di domanda. Ma ora i lavoratori più e¢ cienti si o¤ riranno in
minor numero, perché si vedono o¤ rire una paga inferiore a quella che avrebbero nel
caso di informazione simmetrica. In maniera simmetrica i lavoratori meno e¢ cienti
si o¤ riranno in maggior numero, perché si vedono o¤ rire una paga superiore a quella
che avrebbero nel caso di informazione simmetrica. Dunque le proporzioni dei due
tipi di lavoratori assunti cambiano, a favore della quota dei meno e¢ cienti: se, dopo
aver sperimentato l’e¤ ettiva qualità dei suoi lavoratori, la Medium Job deduce che la
probabilità di trovare lavoratori e¢ cienti è inferiore a 1/ 2, la settimana successiva
abbasserà la paga o¤ erta. Procedendo così, sul mercato potrebbero rimanere solo lavoratori poco e¢ cienti e con paga bassa (“selezione avversa”): è scomparso il mercato
dei lavoratori più e¢ cienti, e con esso il relativo surplus sociale, che sarebbe invece
esistito in caso di informazione simmetrica.
(3) E’ interesse dei lavoratori più e¢ cienti convincere la Medium Job di essere
tali. Un modo ‘economicamente’e¢ cace per fornire una ‘garanzia’alla Medium Job
è essere disposti ad accettare un contratto in cui, per esempio, vengono inizialmente
pagati con paga elevata, ma poi accetteranno un’ampia riduzione di paga (scendendo
sotto la paga di un lavoratore non e¢ ciente) se si scopre che non sono e¢ cienti.
I lavoratori non e¢ cienti non accetterebbero un contratto di questo tipo, in quanto
sono certi che dovranno poi accettare una paga inferiore al loro valore. Accettare quel
contratto è dunque un ‘segnale’ credibile di qualità elevata.
6
Esercizio 4. Si discuta del modello di scelta sotto incertezza. In particolare: (1)
si de…niscano le nozioni di variabile casuale, o lotteria, valore atteso e varianza,
spiegando quali caratteristiche del problema di scelta le due ultime misurano; (2)
si de…nisca la nozione avversione al rischio, usando solo le nozioni individuate al
punto precedente e senza fare gra…ci; (3) si de…nisca la nozione di utilità attesa;
utilizzando il “principio dell’utilità attesa”, si dimostri che una funzione di utilità
concava rappresenta e¤ettivamente le preferenze di un avverso al rischio.
Soluzioni. (1) Si parla di scelta sotto incertezza quando gli esiti delle proprie
scelte non sono noti con certezza nel momento in cui le si prende, vale a dire che
dopo aver compiuto una scelta interviene ancora qualche evento casuale in grado
di in‡uenzare l’esito. L’esito stesso, dunque, può essere visto come una variabile
casuale, cioè una variabile che potrà assumere uno tra un certo numero di valori,
ciascuno con una certa probabilità. La probabilità di ognuno dei valori è un numero
compreso fra zero e uno; una probabilità maggiore indica che c’è maggior …ducia che
nella possibilità che quel valore si veri…chi. Una lotteria è una variabile casuale i cui
valori sono somme monetarie. Il valore atteso (VA) di una lotteria è il valore che in
media ci si aspetta di vincere, e si calcola come media ponderata dei diversi valori,
con pesi dati dalle corrispondenti probabilità. La varianza di una lotteria misura il
suo rischio, vale a dire il fatto che con quella lotteria si possa vincere molto ma anche
perdere molto; la varianza è la media ponderata (con le probabilità) delle distanze al
quadrato dei diversi esiti dal loro valore atteso.
(2) Si dice avverso al rischio un soggetto che fra due lotterie con il medesimo
valore atteso preferisce quella con minor varianza.
(3) Se un soggetto può fruire di una certa somma monetaria, per valutare il suo
benessere non usiamo la somma monetaria, ma l’utilità che quel soggetto ricava dalla
somma monetaria stessa. Una funzione di utilità è una funzione che dice qual è il
livello di utilità (un numero) che corrisponde al possesso di ogni possibile somma
monetaria. È ragionevole supporre che una funzione di utilità sia crescente. Allora,
un soggetto che a¤ ronta una lotteria è interessato non tanto alle somme monetarie
che potrà ottenere quanto alle utilità che ne deriveranno. Ecco allora che la variabile
casuale che davvero interessa a quel soggetto è in termini di utilità: una variabile casuale con valori pari alle utilità delle diverse somme monetarie, e con probabilità pari
alle corrispondenti somme monetarie stesse. Essendo l’utilità una variabile casuale,
se ne può calcolare il valore atteso, che si chiama utilità attesa (UA). Il principio
dell’utilità attesa a¤ erma che ogni soggetto, di fronte a diverse lotterie, sceglie quella
che gli dà massima utilità attesa. Se la funzione di utilità di un individuo è concava,
gli archi giacciono sopra la corrispondente corda (vedi gra…co)
7
U
U(A)
U(VA)
UA
U(B)
B
VA
M
A
In questo caso l’individuo preferisce strettamente disporre con certezza della somma
VA piuttosto che partecipare ad una lotteria con analogo valore atteso; infatti
U (V A) > U A
Dato che la varianza associata all’opzione "disporre con certezza della somma VA" è
nulla mentre la varianza associata all’opzione "partecipare ad una lotteria con esito
atteso VA" è positiva, l’individuo è e¤ ettivamente avverso al rischio.
p
Esercizio 5. La funzione di utilità di Antonio è data da U (X) = Xdove X indica
il reddito percepito. Antonio ha due possibilità lavorative: diventare un impiegato
di banca ed ottenere 100 euro/ora; avviare un’attività in proprio ed ottenere 400
euro/ora nel 20% dei casi (25 euro/ora altrimenti). (1) Caratterizzate l’atteggiamento
di Antonio rispetto al rischio e calcolate il reddito orario che Antonio si aspetta
di ottenere nelle due opzioni lavorative. (2) De…nite e calcolate l’utilità attesa di
Antonio in corrispondenza delle due opzioni lavorative. In base ai risultati ottenuti,
quale carriera verrà scelta? (3) Mario è neutrale al rischio mentre Alberto è amante
del rischio. Qualora venissero loro o¤erte le medesime opzioni lavorative presentate
ad Antonio, cosa deciderebbero di fare? Argomentate la risposta.
Soluzioni. (1) Dal momento che Antonio si caratterizza per una funzione di
utilità crescente e concava,
dU (X)
dX
= 21 X
0:5
> 0e
d2 U (X)
(dX)2
=
1
4X
1:5
< 0;
egli è avverso al rischio. Nel caso in cui scelga la prima opzione lavorativa Antonio
otterrà con certezza 100 euro/ora. Il valore atteso del reddito in corrispondenza della
seconda opzione è invece
EV 2 = (400) 20 % + 25
80 % = 80 + 20 = 100
(2) L’utilità attesa associata alle due opzioni lavorative è
EU1 = U (100) = 10
EU2 = U (400)
20% + U (25)
80% = 4 + 4 = 8
Dato che EU1 > EU2 Antonio preferirà la carriera di impiegato di banca. Trattandosi
di individua avverso al rischio, dovendo scegliere tra due lotterie caratterizzate dal
medesimo valore atteso sceglie sempre quella a minor varianza.
8
(3) Dato che le due carriere si caratterizzano per il medesimo valore atteso, gli
individui neurali al rischio, come Mario, saranno indi¤ erenti tra le due prospettive
lavorative mentre quelli amanti del rischio, come Antonio, preferiranno certamente
la seconda prospettiva alla prima.
Esercizio 6. Nel Paese A ci sono due gruppi di consumatori p
(gruppo 1 e gruppo
2) caratterizzati dalla medesima funzione di utilità U (M ) = M , dove M = 36
euro è il livello iniziale di ricchezza di ciascun consumatore. Entrambi i gruppi
sono esposti ad una perdita di 20 euro ma la stessa si veri…cherà nel 50% dei casi
per i consumatori del primo gruppo e solo nel 10% dei casi per quelli del secondo
gruppo. (1) Come si può caratterizzare l’atteggiamento dei due gruppi di consumatori
rispetto al rischio? Calcolate il valore atteso e l’utilità attesa per le due categorie di
consumatori. (2) Fornite una rappresentazione gra…ca della funzione di utilità dei due
gruppi di consumatori e riportate i valori calcolati al punto precedente. (3) Qual è la
massima cifra che i consumatori appartenenti al primo gruppo sono disposti a versare
per assicurarsi contro il rischio di subire la perdita? Vi aspettate che i consumatori
del secondo gruppo siano disposti a versare la stessa cifra, una cifra maggiore o una
cifra inferiore? Argomentate la risposta.
Soluzioni. (1)-(2) Dal momento che i due gruppi di consumatori si caratterizzano per la medesima funzione di utilità e che la suddetta risulta crescente e concava,
dU (M )
dM
= 12 M
0:5
> 0e
d2 U (M )
(dM )2
=
1
4M
1:5
< 0;
si tratta di individui avversi al rischio. Il valore atteso (EV) è de…nito come a somma
di tutti i possibili risultati di una lotteria, ponderata in funzione delle rispettive probabilità di veri…carsi. Per quanto concerne il primo gruppo di consumatori, essi si
attendono una ricchezza pari a
EV1 = (M
20)
50% + M
50% = 36
10 = 26
90% = 36
2 = 34
mentre il secondo gruppo di consumatori
EV2 = (M
20)
10% + M
Con riferimento all’utilità attesa, il primo gruppo di consumatori ha
EU1 = U (M
20)
50% + U (M )
50% = 2 + 3 = 5
mentre il secondo
EU2 = U (M
20)
10% + U (M )
90% =
2
5
+
Gra…camente
U(M)
Funzione di
utilità
6
EU2
EU1
4
16
EV1
EV2 36
9
M
27
5
=
29
5
(3) Dal momento che i consumatori del primo gruppo otterrebbero un’utilità pari
ad EU1 avendo a disposizione con certezza una somma pari a 25
p
EU1 = U (X) ) 5 = X ) X = 25;
ne consegue che saranno disposti a versare …no ad un massimo di 11 euro
M
X = 36
25 = 11
per assicurarsi contro il rischio di perdite. Tale assicurazione infatti garantirà loro
una ricchezza disponibile pari a 25 in qualunque stato del mondo.
(4) Pur essendo caratterizzati dalla medesima avversione al rischio, i consumatori del secondo gruppo sono meno esposti al rischio di perdite; conseguentemente la
somma massima che saranno disposti a versare per un’assicurazione contro il rischio
di perdite sarà certamente inferiore a quella trovata al punto 3.
Esercizio 7. La serra “Green Finger” acquista dai produttori olandesi bulbi di
tulipani da rivendere in Italia ai propri clienti. Il 60% dei produttori è di bassa
qualità, mentre nel 40% dei casi i bulbi sono di ottima specie. Il proprietario non è
in grado di distinguere a priori tra prodotti di buona o bassa qualità. Egli sarebbe
disposto a pagare …no a 10 euro per un bulbo di tulipano di buona qualità, ma solo
4 euro per un bulbo di bassa qualità. (1) Quanto è disposto a pagare il proprietario
della serra per un bulbo di tulipano? (2) Supponete che un bulbo di alta qualità sia
venduto ad un prezzo non inferiore a 7 euro mentre un bulbo di bassa qualità possa
essere venduto ad un prezzo non inferiore 6 euro. Quale tipo di bulbi vi aspettate
che possa comprare il proprietario della serra? Perché? (3) A tutela dei produttori
di bulbi di alta qualità, l’Unione Europea introduce una certi…cazione di qualità sui
bulbi di tulipano. Qual è la massima disponibilità a pagare del gestore della serra per
un bulbo di tulipano certi…cato? e quanto per uno non certi…cato? (4) Ritenete che
il suplus dei consumatori sia maggiore in presenza o in assenza della certi…cazione di
qualità? Argomentate la risposta.
Soluzioni. (1) Dal momento che a causa dell’asimmetria informativa il proprietario della serra non è in grado di distinguere la qualità delle due tipologie di bulbi, il
prezzo massimo che è disposto a pagare per acquistare bulbi di tulipano olandesi è una
media ponderata della massima disponibilità a pagare per bassa ed alta qualità, i cui
pesi sono dati dalla probabilità di reperire sul mercato i due prodotti. Formalmemente
p = 10 40% + 4 60%
| {z } | {z }
(1)
(2)
dove (1) è ottenuto come prodotto tra la massima disponibilità a pagare per un bulbo
di alta qualità (10 euro) e la probabilità di trovare sul mercato un bulbo di alta qualità
(40%); e (2) è il prodotto tra la massima disponibilità a pagare per un bulbo di bassa
qualità (4 euro) e la probabilità di trovare sul mercato un bulbo di bassa qualità (60%).
Quindi il prezzo massimo con asimmetria informativa è
p = 10
40% + 4
60% = 4 + 2; 4 = 6; 4
Dal momento che il prezzo massimo che il proprietario della serra è disposto a
pagare è inferiore al prezzo minimo al quale i bulbi di alta qualità sono venduti, ci
aspettiamo che acquisti solo bulbi di bassa qualità (per i quali, tra l’altro, sarebbe
disposto a pagare solo 4 euro).
10
(3) Se il certi…cato è garanzia di alta qualità, il proprietario della serra sarebbe
disposto a pagare …no ad un massimo di 10 euro per un bulbo certi…cato (in quanto
avrebbe la garanzia che il bulbo acquistato sia di alta qualità) e …no ad un massim
di 4 euro per un bulbo privo di certi…cazione (l’assenza d certi…cazione è interpretata
come segnale della scarsa qualità del buobo acquistato).
(4) In assenza di certi…cazione, solo i bulbi di bassa qualità vengono venduti sul
mercato (selezione avversa). I bulbi di alta qualità, pur avendo qualcuno disposto
ad aquistarli (10 > 7), non verranno commercializzati con conseguente perdita di
benessere. Si noti che i bulbi di bassa qualità trovano (per un breve periodo - cioè
…ntanto che i consumatori non si accorgono che sul mercato la probabilità di trovare
bulbi di alta qualità è in…ma) spazio nel mercato anche se la disponibilità a pagare
è inferiore al prezzo minimo al quale i rivenditori sono disposti a venderli (6 > 4).
In assenza di certi…cazione, non solo non si vende un prodotto (bulbo di alta qualità)
che avrebbe mercato, ma se ne vende uno (bulbo di bassa qualità) che non dovrebbe
aver mercato e la cui vendita produce una perdita di benessere.
In presenza di certi…cazione, solo i bulbi di alta qualità vengono venduti. I bulbi di
bassa qualità, non avendo nessuno disposto ad acquistarli non saranno prodotti. Sicuramente il surplus dei consumatori sarà più elevato in presenza della certi…cazione.
Esercizio 8. Il proprietario di un magazzino deve decidere se attuare o meno un
programma di prevenzione degli incendi. Si supponga che il valore del magazzino sia
pari a 100 euro. La probabilità di incendio attuando il programma di prevenzione
è del 5%, mentre in assenza di programma di prevenzione la probabilità di incendio
è del 20%. In caso di incendio tutto il magazzino andrà in fumo. (1) Supponendo
che il programma di prevenzione costi 10 euro, ritenete che il proprietario del magazzino decida di attuarlo? Argomentate. (2) Oltre al programma di prevenzione,
il proprietario può sottoscrivere un’assicurazione (attuarialmente equa) che lo risarcisca integralmente in caso di incendio. Si calcoli l’ammontare del premio richiesto
dall’assicurazione in presenza del programma di prevenzione ed in assenza di programma di prevenzione. (3) Il proprietario del magazzino presenta alla compagnia
assicurativa una certi…cazione che attesta la sottoscrizione per l’anno in corso di un
programma di prevenzione. L’assicuratore propone una polizza biennale con premio
annuo pari a 5 euro. Si valuti l’incentivo del proprietario del magazzino ad attuare un
programma di prevenzione nel secondo anno di validità della polizza e l’e¤etto di tale
scelta sui pro…tti della compagnia assicurativa. (4) Si discuta il risultato ottenuto al
punto 3.
Soluzioni. (1) Il valore atteso (EV 1 ) del magazzino in assenza di un programma
di prevenzione è
EV1 = 100 80% + 0 20% = 80;
mentre in presenza di un programma di prevenzione il valore atteso del magazzino
sarebbe pari a
EV2 = 100 95% + 0 5% = 95:
Dal momento che l’attuazione di un programma di prevenzione comporta un aumento
del valore atteso del magazzino di 15 euro
EV2
EV1 = 95
80 = 15;
se tale programma ha un costo non superiore a 15 euro, il proprietario deciderà di
attuarlo.
11
(2) In presenza del programma di prevenzione il premio equo, misurato come il
prodotto tra il danno subito e la probabilità che l’evento dannoso si veri…chi, è
premio1 = 5%
100 = 5
In assenza di un programma di prevenzione il premio equo è
premio2 = 20%
100 = 20
La sottoscrizione di un programma di prevenzione riduce il premio assicurativo richiesto
in quanto riduce la probabilità che l’evento dannoso si veri…chi.
(3)-(4) Consideriamo il secondo anno di validità della polizza. Poichè il proprietario del magazzino è completamente assicurato (sa che in caso di incendio
l’assicurazione provvederà a rimborsarlo integralmente dei danni subiti a prescindere
dalla probabilità con cui l’evento dannoso si veri…cherà), egli non ha più interesse a
sottoscrivere il programma di prevenzione perchè tale programma comporterebbe esclusivamente un esborso di 10 euro. A seguito della mancata sottoscrizione di tale
programma, la probabilità di incendio nel secondo anno sarà pari al 20%, con un
esborso atteso da parte della compagnia assicurativa di
20%
100 = 20 > 5
a fronte di un premio richiesto pari a soli 5 euro. L’assicurazione, a causa del
comportamento negligente dell’assicurato subisce quindi una perdita pari a 15 euro
(20-5=15). Se la compagnia avesse anticipato l’e¤ etto avverso derivante da una
copertura assicurativa biennale, avrebbe proposto
un’assicurazione annua con premio di 5 euro solo in presenza di certi…cazione;
un’assicurazione biennale con premio di 5 euro il primo anno e 20 il secondo;
una copertura parziale del danno (assicurazione con franchigia).
12