Nome file k:\scuola\didattica\corsi\corso fisica\fluidi\equazione di bernoulli 1.doc
Elaborato il 20/09/2004 alle ore 22.55.41, salvato il 18/05/03 1.01
Creato il 09/04/2003 8.13.00
Dimensione file: 48640 byte
stampato il 20/09/2004 22.55.00
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
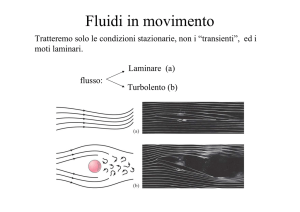
Equazione di Bernoulli
Conservazione dell’energia per un fluido che scorre con moto
laminare all’interno di un condotto di sezione variabile, con asse
ad altezza costante.
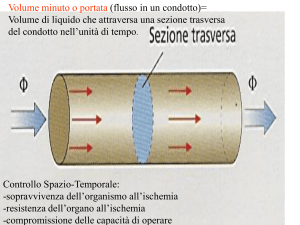
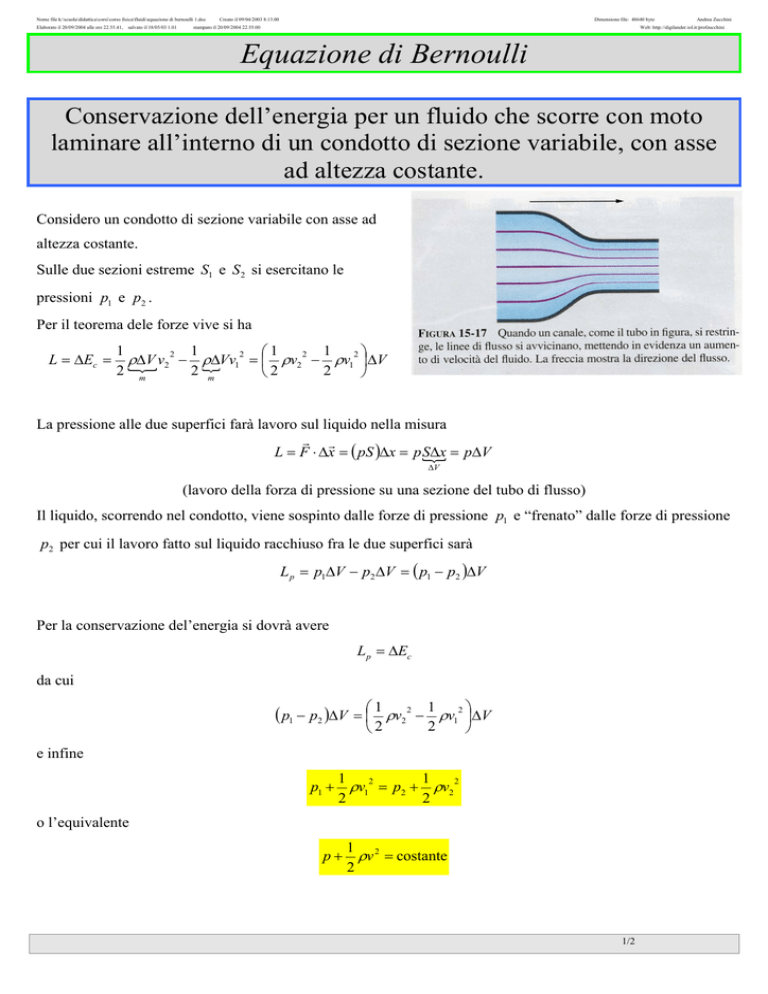
Considero un condotto di sezione variabile con asse ad
altezza costante.
Sulle due sezioni estreme S1 e S 2 si esercitano le
pressioni p1 e p2 .
Per il teorema dele forze vive si ha
L = ∆Ec =
1
1
1 2⎞
⎛1
2
2
ρ∆V v2 2 − ρ
∆Vv1 = ⎜ ρv2 − ρv1 ⎟∆V
{
{
2 m
2 m
2
⎝2
⎠
La pressione alle due superfici farà lavoro sul liquido nella misura
r r
L = F ⋅ ∆x = ( pS )∆x = p S{
∆x = p∆V
∆V
(lavoro della forza di pressione su una sezione del tubo di flusso)
Il liquido, scorrendo nel condotto, viene sospinto dalle forze di pressione p1 e “frenato” dalle forze di pressione
p2 per cui il lavoro fatto sul liquido racchiuso fra le due superfici sarà
L p = p1∆V − p2 ∆V = ( p1 − p2 )∆V
Per la conservazione del’energia si dovrà avere
L p = ∆Ec
da cui
( p1 − p2 )∆V
1 2⎞
⎛1
2
= ⎜ ρv2 − ρv1 ⎟∆V
2
⎝2
⎠
e infine
1 2
1
2
p1 + ρv1 = p2 + ρv2
2
2
o l’equivalente
p+
1 2
ρv = costante
2
1/2
Nome file k:\scuola\didattica\corsi\corso fisica\fluidi\equazione di bernoulli 1.doc
Elaborato il 20/09/2004 alle ore 22.55.41, salvato il 18/05/03 1.01
Creato il 09/04/2003 8.13.00
Dimensione file: 48640 byte
stampato il 20/09/2004 22.55.00
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
Conservazione dell’energia per un fluido che scorre con moto
laminare all’interno di un condotto di sezione e altezza variabili
In questo secondo caso dovremo tenere presente che
oltre a quanto già considerato ci sarà anche la forza
gravitazionale che farà lavoro e che quindi dovrà essere
considerata nel bilancio energetico.
Come prima, avremo
L = ∆Ec =
1
1
1
⎛1
⎞
ρ∆V v2 2 − {
ρ∆Vv12 = ⎜ ρv2 2 − ρv12 ⎟∆V
{
2 m
2 m
2
⎝2
⎠
(Teorema delle forze vive)
L p = p1∆V − p2 ∆V = ( p1 − p2 )∆V
(lavoro delle forze di pressione)
e in aggiunta
⎛
⎞
⎟
∆
−
∆
Lg = −⎜ ρ
V
gh
ρ
V
gh
2
1
{ ⎟
⎜{
m
⎝ m
⎠
(lavoro della forza di gravità)
Si dovrà avere allora
L = Lg + L p = ∆Ec
da cui
1 2⎞
⎛1
2
⎜ ρv2 − ρv1 ⎟∆V = ( p1 − p2 )∆V − (ρgh2 − ρgh1 )∆V
2
⎝2
⎠
e semplificando infine
1 2
1
2
p1 + ρgh1 + ρv1 = p2 + ρgh2 + ρv2
2
2
(Equazione di Bernoulli)
2/2