Idrodinamica Equazione di con0nuità Equazione di Bernoulli Fluidi Ideali Lo studio del moto di un fluido reale
sarebbe troppo complesso ed è ancora
oggetto di molti studi. Limitiamoci a
studiare un liquido reale che sia
vincolato alle seguenti caratteristiche.
Supponiamo che il nostro fluido sia:
• Incoprimibile, cioè sia un liquido e che la massa volumica sia
costante
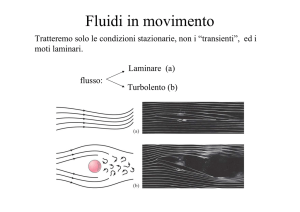
• Laminare, cioè nel tempo non cambi ne direzione ne verso: il
moto dell’acqua al centro di un fiume è laminare, mentre non lo è
quello delle rapide.
• non viscoso, la viscosità è l’equivalente dell’attrito nel moto dei
solidi. In un fluido ideale l’elica di una barca sarebbe inutile, ma una
barca non avrebbe bisogno di un’elica una volta in movimento.
• Irrotazionale, cioè nel suo movimento il liquido non incontra vortici
Equazione di con0nuità • Consideriamo un liquido che fluisce in un
tubo seguendo le specifiche del fluido
ideale e vediamo come varia la sua velocità
nel caso che il tubo cambi dimensione.
• Supponiamo che nell’intervallo di tempo
Δt una certa quantità di liquido ΔV che
occupa una regione di spazio con
superficie A1 abbia una velocità v1.
• Allora per l’incomprimibilità del liquido la
stessa quantità di liquido dovrà lasciare la
sezione A2, ma la sua velocità sarà diversa.
• Infatti, sia ΔV la quantità di liquido considerata, allora ΔV = A Δx
ovvero ΔV = A vΔt e quindi nel tempo Δt sarà anche A1v1 = A2v2
cioè la portata volumica in [m3/s] è Rv = cost .
• La portata massica espressa in [kg/s] è Rm = ρRv = ρ A v = cost
Equazione di Bernoulli Supponiamo un tubo di flusso che abbia
l’ingresso e l’uscita a due diverse quote e
siano di due diverse sezioni.
Bernoulli partendo dall’equazione di continuità
e facendo semplici considerazioni di
conservazione dell’Energia meccanica
concluse che:
1 2
1 2
p1 + ρv1 + ρgy1 = p2 + ρv2 + ρgy 2
2
2
ovvero
1 2
p + ρv + ρgy = cost
2
Generalità dell’Equazione di Bernoulli Questa equazione ha interessanti implicazioni:
1. Se il fluido è a riposo v1 = v2 ovvero v = 0
p1 - p2 = ρg (y2 – y1)
Questa formula è esattamente uguale all’equazione usata da
Torricelli per misurare la pressione atmosfera
2. Se invece il flusso è orizzontale y1 = y2
p1 – p2 = ½ρ (v22 – v12)
Si verifica l’affermazione che laddove aumenta
la velocità di un fluido diminuisce la
pressione (portanza delle ali, tubo di
venturi)
Si può notare che l’equazione di Bernoulli non ha le dimensioni
dell’energia, ma da questa deriva e vedremo come.
Dimostrazione dell’Equazione di Bernoulli
• In un certo intervallo di tempo Δt ai due
estremi del tubo le superfici che si spostano
sono Δs1 e Δs2 e per il principio di continuità
dovrà essere: ΔV = Δs1A1 = Δs2A2.
• Il lavoro fatto sarà
w = p1A1Δs1 - p2A2Δs2 = w = (p1-p2) ΔV.
(In s2 la pressione è diretta in senso opposto alla
pressione in s1, quindi segno - in s2 )
• Il lavoro fatto corrisponde alla variazione
dell’energia meccanica.
w = E+U
Ancora sull’equazione di Bernoulli
• D’altronde l’Ek(s1) = ½ mv2 = ½ ρ ΔV v12 è
l’energia cinetica di una massa m che entra nel
tubo di flusso in s1.
• Nello stesso intervallo di tempo la stessa massa
dovrà lasciare il tubo da s2 portandosi dietro una
energia cinetica Ek(s2) così che possiamo scrivere
ΔEk = Ek(s2) – Ek(s1) = ½ ρ ΔV (v22 - v12)
• L’energia potenziale della massa m entrante in
s1 sarà Δmgy1 = ρ ΔVgy1 e quella uscente in s2
nello stesso Δt sarà Δmgy2 = ρ ΔVgy2
ΔU = ρ ΔV g(y2 – y1)
• Per il teorema del Lavoro e dell’Energia
(p1-p2) ΔV = ½ ρ ΔV (v22-v12) + ρ ΔV g(y2 - y1)
o più semplicemente
p + ½ ρv2 + ρgy = cost
[M-1KS-2]
Esempio classico Trovare la velocità dell’acqua che esce dal foro?
1.
Bisogna pensare ad un tubo con diametro del
serbatoio. Quindi per l’equazione della continuità
Av0 = av
v0 = (a/A) v
2. p0 + ½ ρ v02 + ρ gh = p0 + ½ ρ v2 + ρ g(0)
v = (2gh)½
e per v0<<v
(velocità di un grave)
Come pesare la spinta di Archimede Un recipiente pieno d’acqua è posto su una bilancia che indica un peso W.
Una pietra che pesa w, agganciata ad una corda, viene immersa nell’acqua
senza toccare il fondo.
La pietra sospesa ad un filo e immersa
nell’acqua deve rispettare la II legge di
Newton e pertanto Σ Fx = 0 e le forze
presenti sono: la forza peso w, la
tensione del filo T e la forza di
galleggiamento B, quindi T + B = w (*).
Quando mettiamo il sistema isolato sulla
bilancia, la molla eserciterà sul sistema
una forza S così che la II legge di
Newton darà W + w = S + T e tenendo conto della relazione (*) avremo:
W + (T + B) = S + T
S=W+B
B = ρ g V spinta di Archimede
la bilancia segnerà la forza peso dell’acqua più la spinta di Archimede