3 Geometria delle masse e momento di 2° ordine
3.2 Momento d’inerzia di superfici piane e modulo di resistenza
1
3.2.1 Momenti di inerzia assiali di superfici piane regolari
Parallelogramma
Momento d’inerzia rispetto
a un asse tangente a un lato
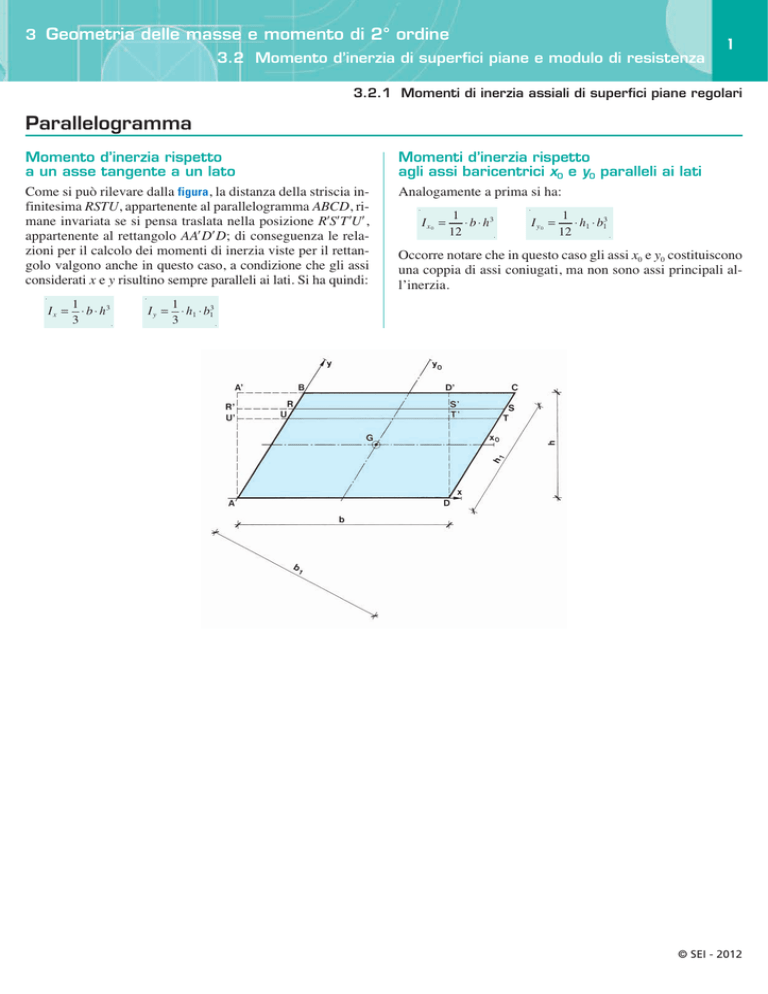
Come si può rilevare dalla figura, la distanza della striscia infinitesima RSTU, appartenente al parallelogramma ABCD, rimane invariata se si pensa traslata nella posizione R⬘S⬘T⬘U⬘,
appartenente al rettangolo AA⬘D⬘D; di conseguenza le relazioni per il calcolo dei momenti di inerzia viste per il rettangolo valgono anche in questo caso, a condizione che gli assi
considerati x e y risultino sempre paralleli ai lati. Si ha quindi:
Ix =
1
⋅ b ⋅ h3
3
Iy =
Momenti d’inerzia rispetto
agli assi baricentrici x0 e y0 paralleli ai lati
Analogamente a prima si ha:
Ix =
0
1
⋅ b ⋅ h3
12
Iy =
0
1
⋅ h1 ⋅ b13
12
Occorre notare che in questo caso gli assi x0 e y0 costituiscono
una coppia di assi coniugati, ma non sono assi principali all’inerzia.
1
⋅ h1 ⋅ b13
3
© SEI - 2012












