Funzioni quadratiche con GeoGebra
•
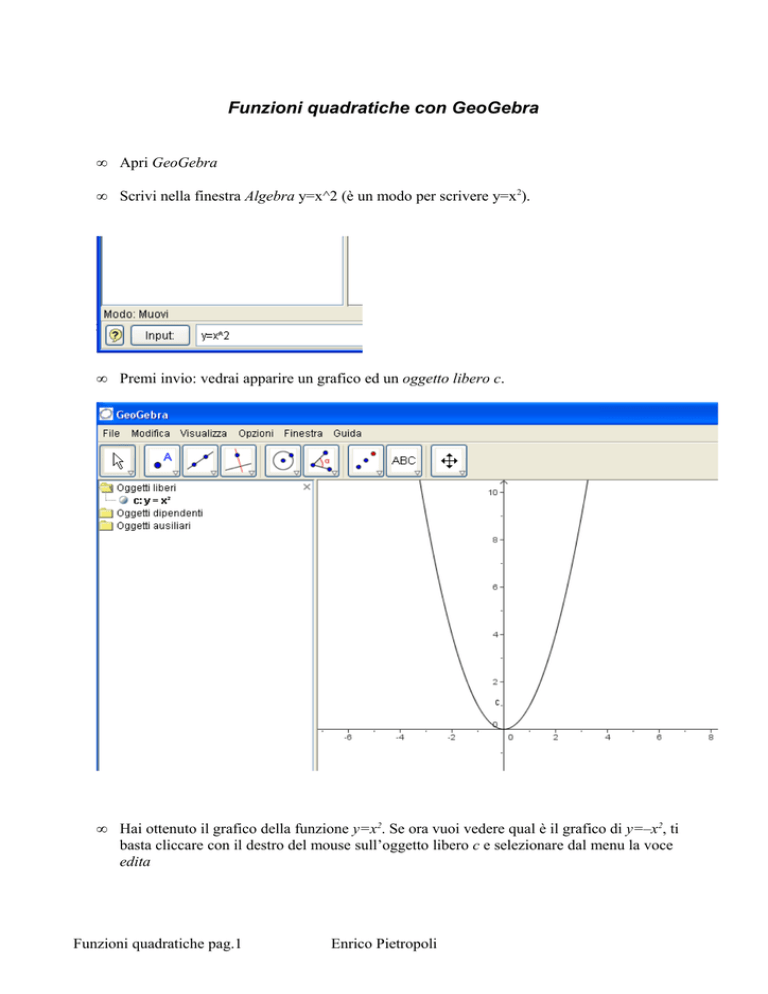
Apri GeoGebra
•
Scrivi nella finestra Algebra y=x^2 (è un modo per scrivere y=x2).
•
Premi invio: vedrai apparire un grafico ed un oggetto libero c.
•
Hai ottenuto il grafico della funzione y=x2. Se ora vuoi vedere qual è il grafico di y=–x2, ti
basta cliccare con il destro del mouse sull’oggetto libero c e selezionare dal menu la voce
edita
Funzioni quadratiche pag.1
Enrico Pietropoli
•
Correggi ora l’equazione inserendo il segno ‘– ‘ dopo il segno ‘=’ e premi invio: il grafico
precedente verrà sostituito dal grafico della funzione y=–x2
•
Puoi ulteriormente indagare i grafici delle funzioni quadratiche, magari studiando la
funzione y=2x2. (Scrivi nella finestra algebra y=2*x^2). Sia questa, che la funzione
precedente, sono ottenute dalla funzione iniziale mediante trasformazioni geometriche che
dovresti conoscere. Sul tuo libro di testo trovi le equazioni ed i nomi delle trasformazioni.
•
Sei ora pronto per studiare il grafico di una qualunque funzione di 2° grado del tipo
y=ax2+bx+c: per fare questo ti conviene aprire un nuovo file GeoGebra e scrivere, nella
Funzioni quadratiche pag.2
Enrico Pietropoli
finestra Algebra, dei valori a tua scelta per i parametri a, b, c. Scrivi, ad esempio, a=1 e
premi invio, b=2 e premi invio, c=3 e premi invio; troverai i tre oggetti liberi a, b, c.
•
Ora scrivi nella finestra Algebra l’equazione y=a*x^2+b*x+c e premi invio: appare
l’oggetto dipendente d, cioè l’equazione y=x2+2x+3 e il grafico relativo
Funzioni quadratiche pag.3
Enrico Pietropoli
•
Ora puoi modificare i valori dei parametri a, b, c cliccando su di essi con il destro del mouse
e selezionando dal menu la voce edita: il grafico cambierà corrispondentemente. Salva il file
con il nome grafico dipendente.
•
Ora apri un nuovo file GeoGebra e scrivi, nella finestra Algebra, y=x^2+2*x+3 e premi
invio: appare il grafico di prima e l’oggetto libero c corrispondente all’equazione appena
scritta. Rispetto alla costruzione del punto precedente, ora, l’equazione è un oggetto libero.
Puoi cliccare con il sinistro del mouse sul grafico e trascinarlo, osservando variare di
conseguenza i valori del coefficiente della x e del termine noto.
Funzioni quadratiche pag.4
Enrico Pietropoli
•
•
•
Ti sarai ormai accorto che tutti questi grafici “si somigliano”: sono parabole con asse di
b
simmetria verticale. Tale retta ha equazione x = −
.
2a
Le parabole sono definite come il luogo dei punti del piano equidistanti da una retta d
(direttrice) e da un punto F (fuoco). Puoi osservare il significato della definizione mediante
il file “parabola come luogo geometrico”.
b b 2 − 4ac 1
e la direttrice ha equazione
F
;−
+
Il fuoco ha coordinate −
4a
4a
2a
b 2 − 4ac 1
d:y= −
−
4a
4a
•
b b 2 − 4ac
.
;−
La parabola ha un altro punto particolare: il vertice di coordinate V −
4a
2a
Per visualizzare tutti questi elementi sul grafico la cosa migliore è riaprire il file grafico
dipendente precedentemente salvato. Immetti nella finestra Algebra le coordinate del vertice
scrivendo V=(–b/(2*a), – (b^2–4*a*c)/(4*a)).
•
Premi invio. Ora immetti x=–b/(2*a) nella finestra Algebra. Il risultato è il seguente:
•
Funzioni quadratiche pag.5
Enrico Pietropoli
Funzioni quadratiche pag.6
Enrico Pietropoli