grafo ad

AL LUNA PARK
Immaginiamo di andare al Luna Park con i nostri ragazzi e di fermarci presso 3 attrazioni in particolare, per
cui sia necessario il calcolo delle probabilità, la proposta delle attività va via via complicandosi…
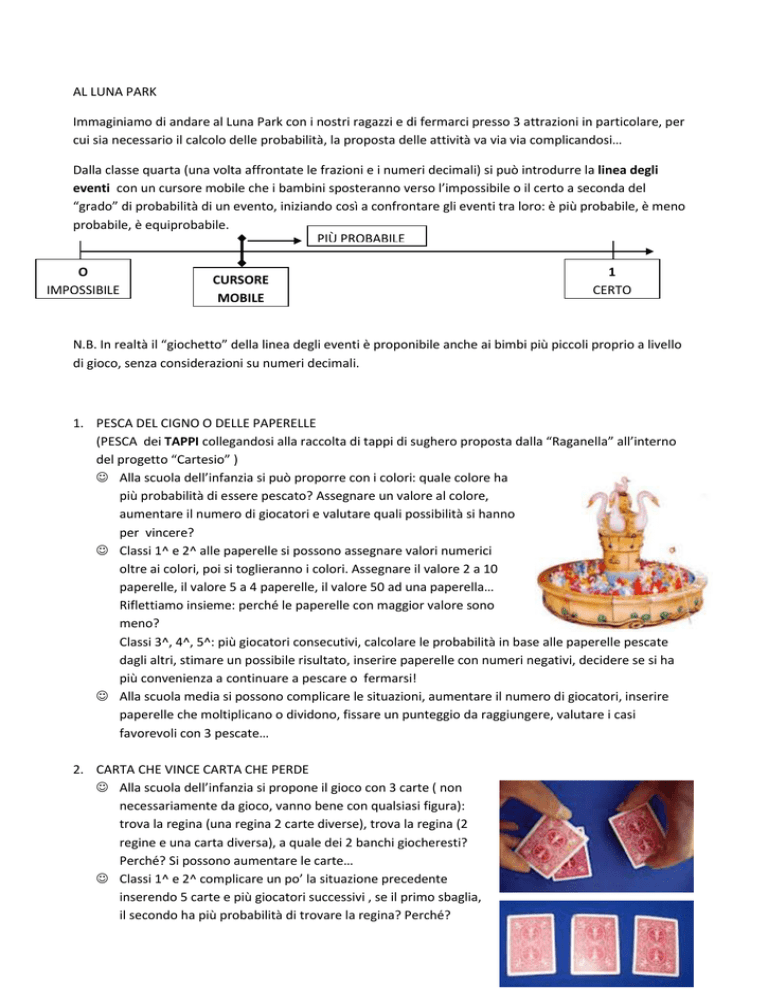
Dalla classe quarta (una volta affrontate le frazioni e i numeri decimali) si può introdurre la linea degli
eventi con un cursore mobile che i bambini sposteranno verso l’impossibile o il certo a seconda del
“grado” di probabilità di un evento, iniziando così a confrontare gli eventi tra loro: è più probabile, è meno
probabile, è equiprobabile.
PIÙ PROBABILE
O
IMPOSSIBILE
CURSORE
MOBILE
1
CERTO
N.B. In realtà il “giochetto” della linea degli eventi è proponibile anche ai bimbi più piccoli proprio a livello
di gioco, senza considerazioni su numeri decimali.
1. PESCA DEL CIGNO O DELLE PAPERELLE
(PESCA dei TAPPI collegandosi alla raccolta di tappi di sughero proposta dalla “Raganella” all’interno
del progetto “Cartesio” )
 Alla scuola dell’infanzia si può proporre con i colori: quale colore ha
più probabilità di essere pescato? Assegnare un valore al colore,
aumentare il numero di giocatori e valutare quali possibilità si hanno
per vincere?
 Classi 1^ e 2^ alle paperelle si possono assegnare valori numerici
oltre ai colori, poi si toglieranno i colori. Assegnare il valore 2 a 10
paperelle, il valore 5 a 4 paperelle, il valore 50 ad una paperella…
Riflettiamo insieme: perché le paperelle con maggior valore sono
meno?
Classi 3^, 4^, 5^: più giocatori consecutivi, calcolare le probabilità in base alle paperelle pescate
dagli altri, stimare un possibile risultato, inserire paperelle con numeri negativi, decidere se si ha
più convenienza a continuare a pescare o fermarsi!
 Alla scuola media si possono complicare le situazioni, aumentare il numero di giocatori, inserire
paperelle che moltiplicano o dividono, fissare un punteggio da raggiungere, valutare i casi
favorevoli con 3 pescate…
2. CARTA CHE VINCE CARTA CHE PERDE
 Alla scuola dell’infanzia si propone il gioco con 3 carte ( non
necessariamente da gioco, vanno bene con qualsiasi figura):
trova la regina (una regina 2 carte diverse), trova la regina (2
regine e una carta diversa), a quale dei 2 banchi giocheresti?
Perché? Si possono aumentare le carte…
 Classi 1^ e 2^ complicare un po’ la situazione precedente
inserendo 5 carte e più giocatori successivi , se il primo sbaglia,
il secondo ha più probabilità di trovare la regina? Perché?
Classi 3^, 4^, 5^: più carte vincenti es. le figure oppure carta più
alta: ma si può decidere di pescarne un’altra annullando la
precedente… conviene? Passare al gioco del “7 e mezzo”, con
mazzi di poche carte… decidiamo di andare avanti o fermarci?
Perché?
 Alla scuola media aumentare il numero di carte, inserire carte penalizzanti e carte Jolly…
3. IL MAGO CIALTRONE
Al Luna Park c’è questo mago che dice di prevedere una grande
vincita giocando i seguenti numeri al gioco del lotto…
 Alla scuola dell’infanzia si può proporre un “Lottino”, una
specie di tombola degli animali (o dei fiori, colori, forme…), il
mago dice di puntare su un determinato animale, viene data
la carta al bambino e poi la maestra sorteggia le carte che
vincono. Mettere nel sacchetto della pesca più carte uguali e
vedere chi ha più probabilità di vincere…
Oppure si può pensare che il mago consigli la categoria, la
maestra poi pescherà, se esce una margherita vince chi ha i
fiori…
 Classi 1^ e 2^ oltre alle attività proposte per l’infanzia, il mago consiglia i numeri, ad alcuni bambini
2 ad altri 3, chi ha più probabilità di vincere?
Classi 3^, 4^, 5^: inserire il concetto di “Ambo”, con due numeri, con tre numeri, con quattro
numeri… consigliati dal mago…
 Alla scuola media si può fare uno studio più preciso sul gioco del Lotto, calcolando le probabilità di
vincita e conseguentemente, di quanto viene moltiplicata la posta giocata… Può essere un’ottima
occasione per mettere in guardia i ragazzi verso i pericoli derivanti da questi ed altri giochi
d’azzardo!
SECONDARIA DI 1° g
1.
2.
3.
4.
Probabilità totale di eventi incompatibili
Probabilità totale di eventi compatibili
Probabilità composta di eventi indipendenti
Probabilità composta di eventi dipendenti
1) Le due proposizioni semplici che introducono gli eventi sono congiunte con il connettivo “o” che
assume valore esclusivo poichè essi non si possono verificare contemporaneamente.
Esempio E : l’alunno interrogato ha il nome che inizia con la lettera A
E : l’alunno interrogato ha il nome che inizia con la lettera P
A
P
Dato un elenco di nomi che si può rappresentare con un diagramma di Euler-Venn si osserva che
gli insiemi sonno disgiunti
P (E o E ) = P + P
La probabilità totale è data dalla somma delle probabilità dei singoli eventi.
Se gli insiemi sono complementari, la somma delle probabilità è 1
A
P
(EA)
( EP)
2) Le due proposizioni semplici sono congiunte con il connettivo “o” che assume valore
inclusivo.Gli eventi sono compatibili poichè il verificarsi dell’uno non esclude il verificarsi dell’altro.
Gli insiemi ammettono elementi comuni e quindi intersezione.
Esempio E : l’alunno interrogato è nella prima metà dell’elenco
E : l’alunno interrogato è femmina
G
F
P (E o E ) = P
G
F
(EG)
+P
( EF )
-P
( EG EF)
La probabilità di un evento totale di eventi compatibili è data dalla somma delle probabilità dei
singoli eventi a cui si sottrae la probabilità dei casi presenti nell’intersezione degli eventi
considerati.
3) Le due proposizioni sono congiunte con il connettivo “e”.
Gli insiemi sono disgiunti, il verificarsi dell’evento A non influenza in alcun modo l’evento B.
I due eventi sono indipendenti e la probabilità del loro verificarsi contemporaneo si dice
probabilità composta di E e E
Essa è data dal prodotto delle singole probabilità degli eventi che la compongono
1
P
(E1 e E2)
=P
( E1)
P
2.
(E2)
4) Il verificarsi dell’evento E è condizionato dal verificarsi dell’evento E
la probabilità del verificarsi dell’evento composto di due eventi dipendenti è data dal prodotto della
probabilità del primo evento moltiplicata per quella del secondo evento, condizionato dal verificarsi
del primo.
Per facilitare il calcolo della probabilità si può utilizzare un grafo ad albero come nella figura
sottostante..
2
1
Esempio A) Calcoliamo la probabilità di estrarre due gomitoli blu da un sacchetto che contiene 6
gomitoli verdi e cinque gomitoli blu con due successive estrazioni dopo aver inserito il gomitolo
tolto la prima volta.
E=EeE
dove
E : estrazione di un primo gomitolo blu
E : estrazione di un secondo gomitolo blu
sono eventi indipendenti. Essendo
1
2
1
2
P
( E1)
P
(E )
= 511 P
=P
( E1)
( E2)
= 511
P = 511
(E2)
511 =25121
Esempio B Calcoliamo la probabilità di estrarre due gomitoli blu da un sacchetto che
contiene 6 gomitoli verdi e 5 blu con due successive estrazioni SENZA reinserire il
gomitolo tolto la prima volta
E=EeE
dove
E : estrazione di un primo gomitolo blu
E :estrazione di un secondo gomitolo blu
1
2
1
2
P
( E1)
= 511 P
( E2)
= 410
Dopo che è stato estratto un gomitolo blu e non è stato reinserito nel sacchetto, i casi
favorevoli all’evento E sono rimasti 4 sulla totalità dei casi possibili che ora è 10. Quindi
P = P P = 511 410 =211
2
(E )
( E1)
(E2)
Esercizio 1
Calcola la probabilità che lanciando due dadi si ottenga per somma
E : un numero pari
E : un numero maggiore di 5
E : un numero pari o maggiore di 5
1
2
3
Esercizio 2
Calcola la probabilità che lanciando due dadi si ottenga per somma
E : un numero multipli di 3
E : un numero minore di 4
E : un numero multiplo di 3 o minore di 4
1
2
3
Esercizio 3
Una ditta alimentare decide di incrementare la vendita dei suoi prodotti mettendo in regalo un
anello o una spilla d’oro nei pacchi di biscotti. la ditta garantisce che ogni 500.000 pacchi di biscotti
ci sono 120 anelli e 80 spille. acquistando un pacco di biscotti calcola qual è la probabilità di
E : trovare un anello
E : trovare una spilla
E : trovare un anello o una spilla
1
2
3
Esercizio 4
L’agenda telefonica di Gianna è così suddivisa: l’elenco telefonico dei fratelli (indicato con A),
quello dei vicini di casa (indicato con B) e quello dei genitori (indicato con C)
A {Mauro, Mariagrazia, Mariateresa, Angelo}
B { Mariagrazia, Gianni, Aldo}
C {Elisabetta, Giuseppe}
Mariagrazia è un nome che compare in due elenchi perchè è sia sorella, sia vicina di casa.
prendendo a caso un numero di telefono calcola la probabilità di
E : estrarre il numero di un fratello
E : estrarre il numero di un fratello o di un vicino di casa
E : estrarre il numero di un genitore o di un fratello
E : estrarre il numero di un non parente
1
2
3
4
Esercizio 5
Osserva la ruota della fortuna; in essa sono presenti tre simboli: caramella, palla e scatola, in
quattro diversi colori.
Esercizio 6
Tre giocatori estraggono da un mazzo di 40 carte una carta ciascuno, senza rimettere nel mazzo
quelle già estratte. Calcola la probabilità che il primo giocatore scelga un 7, il secondo un asso di
denari, il terzo un asso di bastoni
Esercizio 7
In una scatola sono contenute 10,matite rosse e 4 verdi, indistinguibili al tatto. calcola la probabilità
che prendendone 3 a caso e e senza rimetterle nella scatola esse siano
3 matite rosse
3 matite verdi
Esercizio 8
In un cofanetto ci sono 14 caramelle al limone e 8 all’arancia. Calcola la probabilità che la prima
estratta sia al limone e la seconda all’arancia nei due casi in cui
la prima caramella sia stata rimessa nel cofanetto
la prima caramella non sia stata rimessa nel cofanetto
Esercizio 9
Un sacchetto contiene 3 palline verdi e 6 palline gialle. calcola la probabilità di estrarre due palline
gialle con due estrazioni successive, senza riporre nel sacchetto la pallina già estratta la prima
volta.
Durata: 8 ore