Simmetrie e funzioni inverse. Attività 1
I. Equazioni di simmetrie assiali
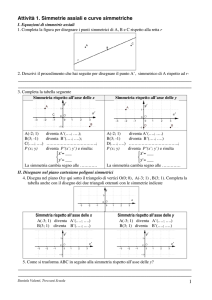
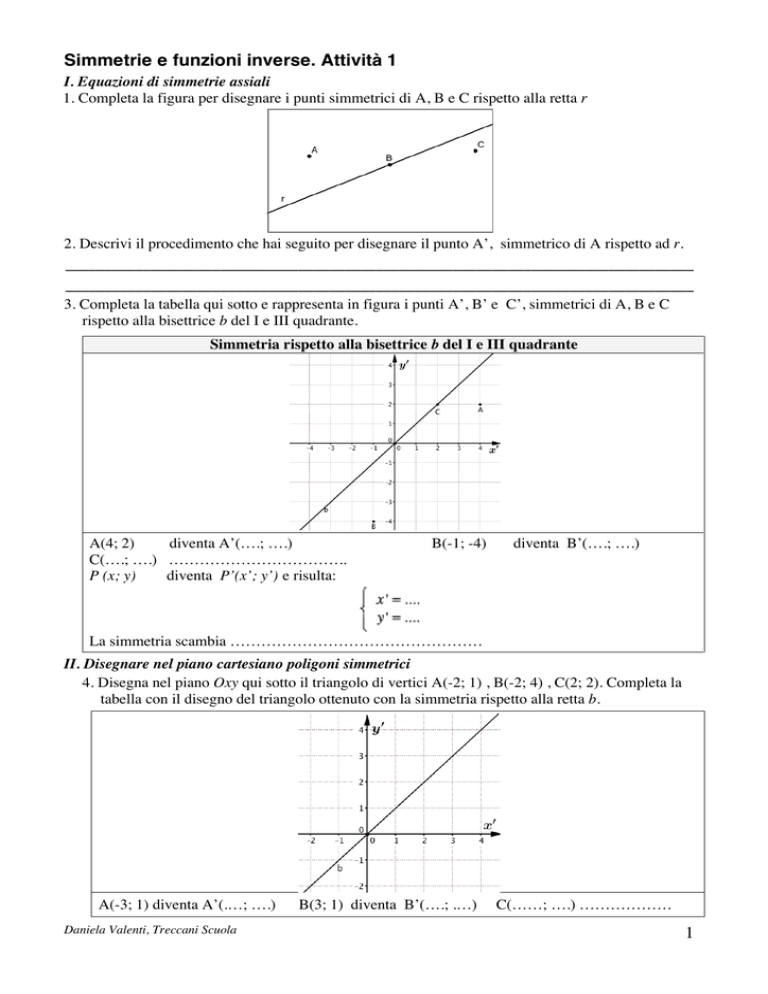
1. Completa la figura per disegnare i punti simmetrici di A, B e C rispetto alla retta r
2. Descrivi il procedimento che hai seguito per disegnare il punto A’, simmetrico di A rispetto ad r.
_________________________________________________________________________________
_________________________________________________________________________________
3. Completa la tabella qui sotto e rappresenta in figura i punti A’, B’ e C’, simmetrici di A, B e C
rispetto alla bisettrice b del I e III quadrante.
Simmetria rispetto alla bisettrice b del I e III quadrante
A(4; 2)
diventa A’(….; ….)
C(….; ….) ……………………………..
P (x; y)
diventa P’(x’; y’) e risulta:
B(-1; -4)
diventa B’(….; ….)
La simmetria scambia ………………………………………….
II. Disegnare nel piano cartesiano poligoni simmetrici
4. Disegna nel piano Oxy qui sotto il triangolo di vertici A(-2; 1) , B(-2; 4) , C(2; 2). Completa la
tabella con il disegno del triangolo ottenuto con la simmetria rispetto alla retta b.
A(-3; 1) diventa A’(.…; ….)
Daniela Valenti, Treccani Scuola
B(3; 1) diventa B’(….; .…)
C(……; ….) ………………
1
III. Disegnare nel piano cartesiano curve simmetriche
5. Disegna nella tabella qui sotto le curve d’equazione data e, a fianco di ogni curva, la sua
simmetrica rispetto alla bisettrice b del I e III quadrante.
Curva d’equazione data
Simmetrica rispetto alla bisettrice b
y = x3
Si scambia ……………………………….
L’equazione della curva è ……………….
La curva è il grafico di una sola funzione?....
y = x2
Si scambia ………………………………
L’equazione della curva è ………………
La curva è il grafico di una sola funzione?....
xy = 1
Si scambia ………………………………
L’equazione della curva è ………………
Che cosa osservi? ……………………….
……………………………………………..
IV. Simmetria assiali con un software di geometria dinamica
6. Apri il file ‘Simmetria2_Scheda1a.ggb’ e procedi nel modo seguente:
• Esplora il comando ‘Simmetria assiale’ per disegnare il simmetrico del triangolo ABC
rispetto alla bisettrice b del I e III quadrante.
• Muovi liberamente i punti A, B e C per osservare le figure ottenute; in particolare che cosa succede se
uno dei punti, ad esempio C arriva sulla bisettrice b? ……………………
7. Apri il file ‘Simmetrie2_Scheda1b.ggb’ e procedi nel modo seguente:
• Clicca su ‘Vista grafica’ e usa il comando ‘Simmetria assiale’ per disegnare la curva simmetrica di
quella già disegnata rispetto alla bisettrice b;
• Clicca su ‘Vista grafica2’ e usa il comando ‘Simmetria assiale’ per disegnare la curva simmetrica di
quella già disegnata rispetto alla bisettrice b.
Daniela Valenti, Treccani Scuola
2