ESAME DI MATEMATICA I
SOLUZIONE DEL TEMA DEL 20 novembre 2003
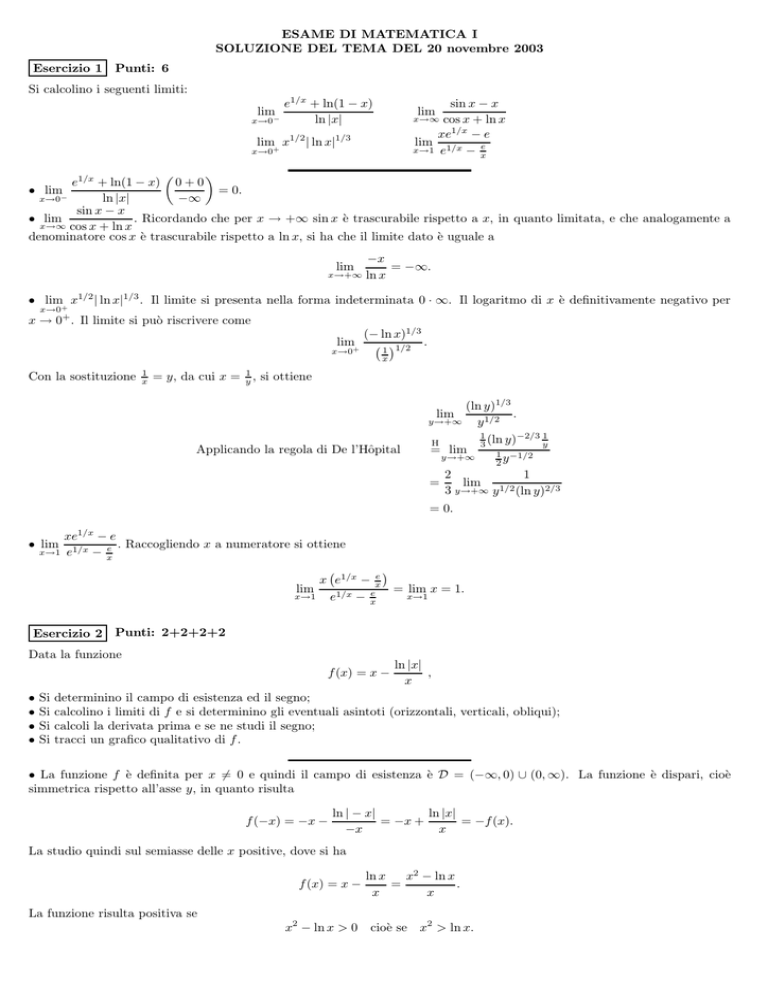
Esercizio 1 Punti: 6
Si calcolino i seguenti limiti:
lim−
x→0
e1/x + ln(1 − x)
ln |x|
sin x − x
cos x + ln x
xe1/x − e
lim
x→1 e1/x − e
x
lim
x→∞
lim x1/2 | ln x|1/3
x→0+
e1/x + ln(1 − x) 0 + 0
= 0.
• lim
ln |x|
−∞
x→0−
sin x − x
. Ricordando che per x → +∞ sin x è trascurabile rispetto a x, in quanto limitata, e che analogamente a
• lim
x→∞ cos x + ln x
denominatore cos x è trascurabile rispetto a ln x, si ha che il limite dato è uguale a
lim
x→+∞
−x
= −∞.
ln x
• lim+ x1/2 | ln x|1/3 . Il limite si presenta nella forma indeterminata 0 · ∞. Il logaritmo di x è definitivamente negativo per
x→0
x → 0+ . Il limite si può riscrivere come
lim+
x→0
Con la sostituzione
1
x
= y, da cui x =
1
y,
si ottiene
(− ln x)1/3
.
1 1/2
x
(ln y)1/3
.
y→+∞
y 1/2
1
−2/3 1
H
3 (ln y)
y
= lim
1 −1/2
y→+∞
y
2
2
1
=
lim
3 y→+∞ y 1/2 (ln y)2/3
= 0.
lim
Applicando la regola di De l’Hôpital
xe1/x − e
. Raccogliendo x a numeratore si ottiene
x→1 e1/x − e
x
• lim
x e1/x − xe
lim
= lim x = 1.
x→1
x→1
e1/x − xe
Esercizio 2 Punti: 2+2+2+2
Data la funzione
f (x) = x −
•
•
•
•
Si
Si
Si
Si
ln |x|
,
x
determinino il campo di esistenza ed il segno;
calcolino i limiti di f e si determinino gli eventuali asintoti (orizzontali, verticali, obliqui);
calcoli la derivata prima e se ne studi il segno;
tracci un grafico qualitativo di f .
• La funzione f è definita per x 6= 0 e quindi il campo di esistenza è D = (−∞, 0) ∪ (0, ∞). La funzione è dispari, cioè
simmetrica rispetto all’asse y, in quanto risulta
f (−x) = −x −
ln | − x|
ln |x|
= −x +
= −f (x).
−x
x
La studio quindi sul semiasse delle x positive, dove si ha
f (x) = x −
x2 − ln x
ln x
=
.
x
x
La funzione risulta positiva se
x2 − ln x > 0
cioè se x2 > ln x.
Tale disuguaglianza è sempre vera per x > 0 dato che risulta
x2 > x − 1 ≥ ln x
(y = x − 1 è l’equazione della retta tangente a ln x in 1).
Pertanto la funzione f è positiva in (0, ∞).
• Vediamo i limiti.
lim f (x) = +∞
x→∞
(ricordando che
ln x
x
→ 0)
lim f (x) = +∞.
x→0+
Quindi l’asse y è asintoto verticale di f .
Vediamo se c’è asintoto obliquo a +∞ Calcolando il
f (x)
ln x
lim
= lim 1 − 2 = 1.
x→∞ x
x→∞
x
Allora calcoliamo il
ln x
lim (f (x) − x) = lim x −
− x = 0.
x→∞
x→∞
x
Pertanto vi è asintoto obliquo a +∞ e la sua equazione è y = x.
• La derivata di f è
y
2
x
(2x − x1 )x − (x2 − ln x)
x2 − ln x
f 0 (x) = D
=
x
x2
2
2x − 1 − x2 + ln x
=
x2
2
x − 1 + ln x
.
=
x2
x
x
1
ln x
x
La derivata è positiva se ln x > 1 − x2 . Da un semplice confronto grafico (a fianco) si
ottiene che la funzione f è crescente per x > 1, decrescente per 0 < x < 1 e che in x = 1 c’è un punto di minimo locale in
cui la funzione vale 1. Si noti che questo è importante per un disegno corretto del grafico: nel punto di minimo la funzione
incerseca l’asintoto.
Studiamo anche la derivata seconda (questo non era richiesto nel tema d’esame). Risulta
(2x + x1 )x2 − (x2 − 1 + ln x)2x
x4
2x3 + x − 2x3 + 2x − 2x ln x
=
x4
3x − 2x ln x
=
x4
3 − 2 ln x
.
=
x3
f 00 (x) =
La derivata seconda è positiva se 3 − 2 ln x > 0, cioè se x < e3/2 , e quindi la funzione f è convessa in (0, e3/2 ), concava in
(e3/2 , ∞) e in x = e3/2 c’è un punto di flesso.
Il grafico è allora il seguente.
y
1
1
e 3/2
x
Esercizio 3 Punti: 1+2
• Sia f : R → R. Si dia la definizione di primitiva di f .
• Si dica se la funzione f (x) = |x| ha primitive e, in caso affermativo, se ne determini una.
• Una primitiva di f è una funzione derivabile g : R → R la cui derivata è uguale a f , cioè tale che g 0 = f in R.
• La funzione f (x) = |x| è continua e quindi, per il teorema fondamentale del calcolo, la funzione
g(x) =
Z
x
f (y) dy =
0
è una primitiva di f .
Risulta
g(x) =
Rx
0 y dy
Rx
0
Per x ≥ 0 si ha g(x) =
Per x < 0 si ha invece
h
i
2 x
y
2
0
=
x2
2 .
Z
g(x) =
0
x
Esercizio 4 Punti: 2+2+2+2
Z 1
1
dx.
• Si calcoli con la definizione
2
0 x ln x
Z
x
|y| dy
0
se x ≥ 0
(−y) dy
y2
y dy =
2
se x < 0.
0
=−
x
• Si dica se è finito
x2
.
2
Z
1
ln sin x dx.
0
• Si studi la convergenza, semplice e assoluta, di
∞
X
(−1)n
n=1
ln n
.
n2
∞
π
X
23n+1
• Si calcoli la somma di
sin
+
2nπ
.
32n+1
2
n=0
• Si tratta di un integrale generalizzato, dato che la funzione integranda non è limitata per x → 0 e per x → 1− . Possiamo
scrivere
Z 1/2
Z 1
Z 1
1
1
1
dx
=
dx
+
dx
2
2
x ln2 x
0
1/2 x ln x
0 x ln x
se entrambi sono finiti.
A parte calcolo le primitive di
1
.
x ln2 x
Si ha
Z
1
1
dx = −
+ c.
2
ln x
x ln x
Quindi
Z
1/2
0
Ora l’altro.
Z
1
1/2
1
dx = lim
a→0+
x ln2 x
Z
1/2
1
dx = lim−
b→1
x ln2 x
Z
b
a
1/2
1/2
1
1
1
1
1
dx = lim −
= lim
+
.
=
2
+
+
ln x a
ln 2 ln a
ln 2
a→0
a→0
x ln x
b
1
1
1
1
=
lim
−
dx
=
lim
−
= ∞.
−
ln x 1/2 b→1−
ln b ln 2
b→1−
x ln2 x
Quindi l’integrale generalizzato non converge.
• Si tratta di un integrale generalizzato in quanto la funzione ln sin x non è limitata per x → 0+ . La funzione è però Riemann
integrabile in ogni intervallo [a, 1] con 0 < a < 1 in quanto è continua. Dimostro che ln sin x è dello stesso ordine di ln x, per
x → 0+ . Infatti si ha
cos x
ln sin x H
x cos x
lim
= lim sin1 x = lim
= 1.
+
+
+
ln
x
sin x
x→0
x→0
x→0
x
Z 1
Quindi per studiare l’integrale dato posso studiare
ln x dx. Si vede facilmente con la definizione che questo converge in
0
quanto, ricordando che le primitive di ln x sono x ln x − x + c,
Z
0
1
ln x dx = lim+ [x ln x − x]1b = lim+ (−1 − b ln b + b) = −1.
b→0
b→0
Quindi l’integrale dato è finito.
• Possiamo vedere prima se la serie converge assolutamente. Consideriamo quindi
Ricordando che per n → ∞ ln n = o(nα ) per ogni α > 0, posso dire che risulta
ln n = o(n1/2 ) e che quindi si ha definitivamente
∞
X
ln n
.
n2
n=1
ln n ≤ n1/2
per n → ∞.
Allora
ln n
n1/2
1
≤
= 3/2 ,
n2
n2
n
che è il termine generale di una serie convergente. Quindi la serie data converge assolutamente e pertanto converge anche
semplicemente.
• Osserviamo intanto che sin π2 + 2nπ = 1 per ogni n. Quindi la serie è
∞
∞
∞ n
∞
X
2 1
2 X 23n
2 X 8n
2X 8
23n+1
= 6.
=
=
=
=
2n+1
2n
n
3
3 n=0 3
3 n=0 9
3 n=0 9
3 1 − 89
n=0
Esercizio 5 Punti: 4
Si dimostri che la funzione
h(x) =
non ha primitive.
n
0
1
x≤0
x>0
Supponiamo che sia H una primitiva di h. Questo vuol dire che H è derivabile e che H 0 = h. Allora
H 0 (0) = h(0) = 0.
Ma, d’altro canto, si ha anche
(per definizione di derivata)
H(x) − H(0)
x
0
= lim+ H (x)
H 0 (0) = lim
(regola di De l’Hôpital)
0
(H = h)
x→0+
x→0
= lim+ h(x)
x→0
=1
(riflettere attentamente sul fatto che sono verificate tutte le ipotesi del teorema di De l’Hôpital).
Pertanto arriviamo ad un assurdo. Non può esistere una primitiva di h. Si noti che non saremmo arrivati ad un assurdo
considerando il limite per x → 0− .
Esercizio 6 Punti: 4
∞
X
ln ln n
(−1)n
Si consideri la serie
, con a ≥ 1 e si dica per quali valori di a essa converge.
n
lna n
n=2
Si tratta di una serie a termini di segno alternato.
∞
X
ln ln n
. Possiamo osservare che si ha
Per a = 1 la serie è
n ln n
n=2
1
ln ln n
≥
definitivamente (per n ≥ ee )
n ln n
n ln n
e che quindi la serie non converge assolutamente. Torneremo su questo caso alla fine e lo studieremo con il criterio di Leibnitz.
Studiamo ora la convergenza assoluta nel caso a > 1.
a−b
Sia 1 < b < a (ad esempio b = a+1
definitivamente. Da questa segue (con x = ln n) che
2 ). Sappiamo che ln x ≤ x
a−b
ln ln n ≤ (ln n)
definitivamente.
Pertanto, definitivamente, si ha
(ln n)a−b
1
ln ln n
≤
=
.
a
a
n ln n
n ln n
n lnb n
Ma questa converge poiché b > 1. Quindi la serie data converge assolutamente e pertanto converge.
ln ln n
Torniamo ora al caso a = 1 e applichiamo il criterio di Leibnitz. Sia bn =
.
n ln n
La successione bn tende a zero per n → ∞ in quanto
0≤
ln n
1
ln ln n
≤
=
n ln n
n ln n
n
e quest’ultima tende da zero.
Dimostro ora che la successione bn è decrescente. Considero la funzione f (x) =
1
x ln x x ln x
− ln ln x(ln x + 1)
ln ln x
e calcolo la sua derivata. Risulta
x ln x
1 − ln ln x(ln x + 1)
.
ln x
x2 ln2 x
Il segno della derivata è dato dal segno del numeratore, che è definitivamente negativo dato che 1 − ln ln x(ln x + 1) tende a
−∞ per x → ∞. Allora la successione bn è definitivamente decrescente e questo basta per applicare il criterio di Leibnitz.
Quindi la serie data converge per tutti gli a ≥ 1.
f 0 (x) =
x2
2
=










