Capitolo 4
Le spettroscopie
1.
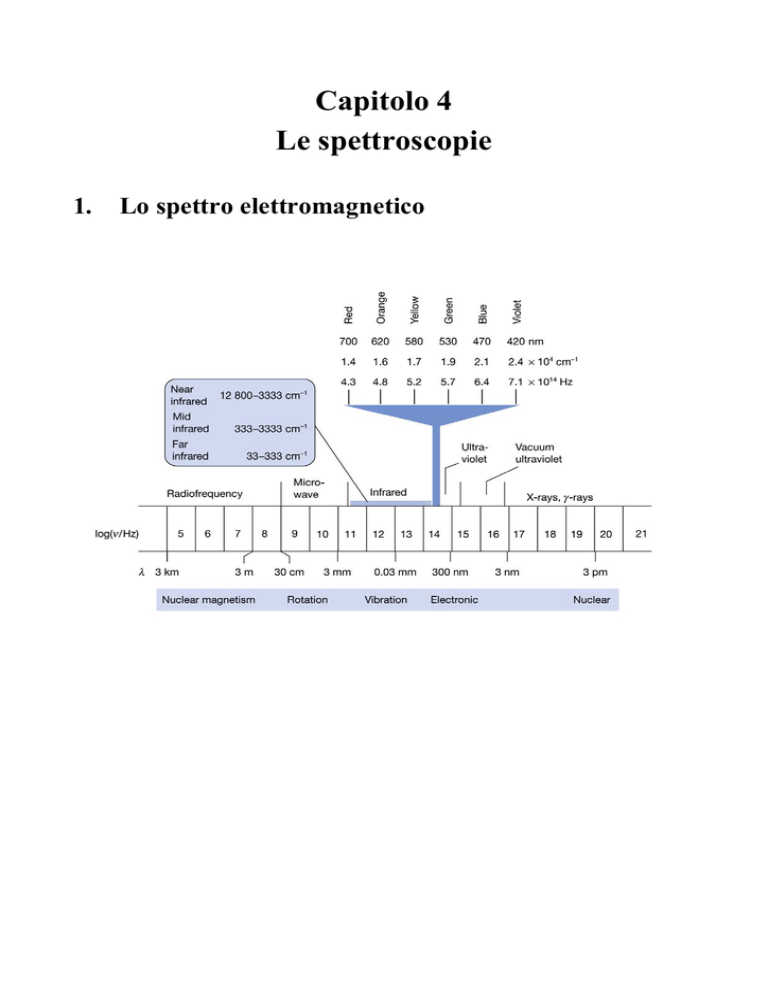
Lo spettro elettromagnetico
2) Tipi di spettroscopia
Emissione:
transizione da livello superiore a livello inferiore
Assorbimento: contrario
2.1 Spettroscopie rotazionali, vibrazionali ed elettroniche
• Spettroscopia a microonde
• Spettroscopia infrarossa (IR)
• Spettroscopia RAMAN (radiazione monocromatica e analisi della
radiazione diffusa)
• Spettroscopia ultravioletta/visibile (UV/VIS)
2.2 Spettroscopie di risonanza
• Risonanza Magnetica Nucleare (NMR)
• Risonanza Paramagnetica Elettronica (EPR/ESR)
Energia del fotone assorbito (condizione di Bohr)
hν = E2 - E1
Lunghezza d'onda
λ=
c
ν
Numero d'onda
ν 1
ν= =
c λ
La scelta della particolare spettroscopia è dettata principalmente da ragioni
ordine pratico (natura del campione, etc.). La spettroscopia Raman si è
diffusa grandemente dopo la scoperta del laser.
Schema generale delle spettroscopie ottiche
2.3 La strumentazione
• La sorgente
lontano IR:
arco a mercurio
vicino IR:
filamento di Nernst (ceramica + terre rare)
VIS:
lampada a tungsteno/iodio o laser
UV:
scarica attraverso gas o laser
Microonde:
Klystron (oscillatore elettromagnetico)
NMR/EPR:
amplificatori
• Il reticolo di diffrazione (prisma)
• Il rivelatore
UV/VIS:
fotomoltiplicatori
IR:
bolometri, arrays di semiconduttori
NMR/EPR:
diodi, circuiti ibridi (tecnologia radar)
3) L'intensità delle linee spettrali
Si definisce trasmittanza, T, il rapporto tra l’intensità di radiazione
trasmessa a una data frequenza e quella incidente
T=
I
I0
La trasmittanza è data dalla legge di Lambert-Beer (relazione empirica)
log
I
I0
= −ε [ J ]l
I = intensità della luce emergente
I0 = intensità della luce incidente
ε = coefficiente molare di assorbimento (coefficiente di estinzione)
l = cammino ottico
J = specie presente nel campione
Il prodotto adimensionale A = ε [J] si definisce assorbanza (un tempo era
chiamato densità ottica).
La legge di Lambert-Beer viene spesso espressa nella forma
I = I 0 × 10 −ε [ J ]l
L'intensità di una riga spettrale dipende dal numero di molecole
che si trovano nello stato iniziale (all'equilibrio) e dalla forza con cui esse
sono in grado di interagire con il campo elettromagnetico (ottico, IR,
microonde...).
3.1 La larghezza delle righe spettrali
a)
Effetto DOPPLER (importante nei gas)
v
ν'' =
1+
s
c
s = velocità della molecola che emette frequenza ν
ν' = frequenza osservata
Per un numero molto elevato di molecole, la riga è Gaussiana e la
sua larghezza a metà altezza è data da
δE =
b)
2λ
2 RTln 2
×
c
M
Allargamento naturale (fenomeno quantistico)
L'indeterminazione dei livelli energetici è correlata con il tempo di
sopravvivenza di un certo stato dal principio di indeterminazione
di Heisenberg
δE ≈
h
τ
esprimendo la dispersione di energia in numeri d'onda si ha la forma
utilizzabile
5.3cm -1
δν ≈
τ ( ps)
c)
Diseccitazione per collisione
Questo processo è dominante a bassa frequenza, poichè il fenomeno
b) ha intensità proporzionale a ν3.
4) Gli spettri vibrazionali
Le transizioni vibrazionali si verificano nella regione infrarossa
dello spettro elettromagnetico: spettroscopia nell’infrarosso
L’energia potenziale di una molecola biatomica nell’intorno della
posizione di equilibrio può essere approssimata da una parabola:
V = 1/2 k (R-Re)2
dove k è la costante di forza del legame.
4.1 I livelli energetici vibrazionali
I livelli energetici vibrazionali di una molecola biatomica di massa
m1+m2 si ottengono risolvendo l’quazione di Schrödinger con il potenziale
dato dalla equazione precedente. Si ottiene:
Eν = (ν + 1/2) hν
ω=
k
µ
ν = 0, 1, 2, ...
µ=
m1m2
m1 + m2
Poichè una tipica transizione vibrazionale ha energia dell’ordine di
10 J, la frequenza della radiazione è dell’ordine di 1014 Hz (infrarosso).
La vibrazione non può essere arrestata totalmente, neppure a 0 K (energia
di punto zero).
-19
4.2 Regole di selezione
Formulazione classica
Per interagire con il campo elettromagnetico perturbante assorbendo
o generando un dipolo di frequenza ω, la molecola deve possedere,
almeno temporaneamente, un dipolo oscillante a quella frequenza.
Non è necessario che la molecola possieda un dipolo permanente. E’
sufficiente che ci sia un cambiamento del momento di dipolo, anche a
partire da zero.
Formulazione quantistica
Le transizioni permesse sono espresse in funzione della variazione
dei numeri quantici. Nel caso delle transizioni vibrazionali si ha ν = ±1.
La variazione di energia che accompagna la transizione da uno stato
a numero quantico ν ad uno a numero quantico ν + 1 sarà ∆Ε = hν.
5) Le transizioni elettroniche: spettri UV e VIS
La distribuzione elettronica delle molecole può essere modificata
con energie dell’ordine di alcuni elettronvolt (1 eV ~ 8000 cm-1). I fotoni
emessi in questo caso cadono nella regione del visibile o dell’ultravioletto.
Esempio: lo spettro di assorbimento della clorofilla
Verde
5.1 Il decadimento degli stati elettronici eccitati
Le molecole eccitate elettronicamente si possono diseccitare per
decadimento radiativo. L’elettrone ricade su un orbitale di energia
inferiore emettendo un fotone. Esistono due modalità principali di
decadimento radiativo: la fluorescenza e la fosforescenza.
Nel caso della fluorescenza, l’emissione cessa spontaneamente non
appena viene meno la radiazione eccitante. La frequenza della
fluorescenza è inferiore rispetto a quella della radiazione incidente,
poichè parte della energia viene dispersa in transizioni vibrazionali.
Nel caso della fosforescenza, invece, l’emissione spontanea può
persistere anche per ore.
Esistono stati quantici di singoletto (spin appaiati) e stati di tripletto
(spin disaccoppiati). Una molecola eccitata mantiene lo stesso stato di
partenza, a meno che non esista un meccanismo di disturbo (es.: campo
magnetico interno) in grado di disappaiare gli spin (intersystem crossing).
In questo caso la molecola non è più in grado di tornare allo stato
fondamentale, poichè nel corso di una transizione lo stato elettronico non
può cambiare (allora si ha la fosforescenza).